注:本篇所用的某些未在本文中实现的函数,或不明确的类,均在上篇博客中有详细过程,因篇幅问题不再赘述。
C++--数据结构--图的相关概念及模拟实现--高阶0712_Gaze!的博客-CSDN博客
1. Dijkstra算法
Dijkstra算法需要开辟两个数组,vector<W>dist 和 vector<int>pPath。
dist存放当前所选定的顶点到其他顶点的距离
pPath存放的是从哪个节点来的,存的是该节点的下标
思路:
将全部顶点分为两个集合S和Q,S是已经确定了最短路径的集合,初始时为空即可。假设进行Dijkstra算法的起始顶点是src,其映射下标是srci,将dist[srci]=0。
每次选取路径最小的,即dist数组内最小的那个值,将dist下标(路径终点顶点)纳入S集合,用该节点再次更新dist数组
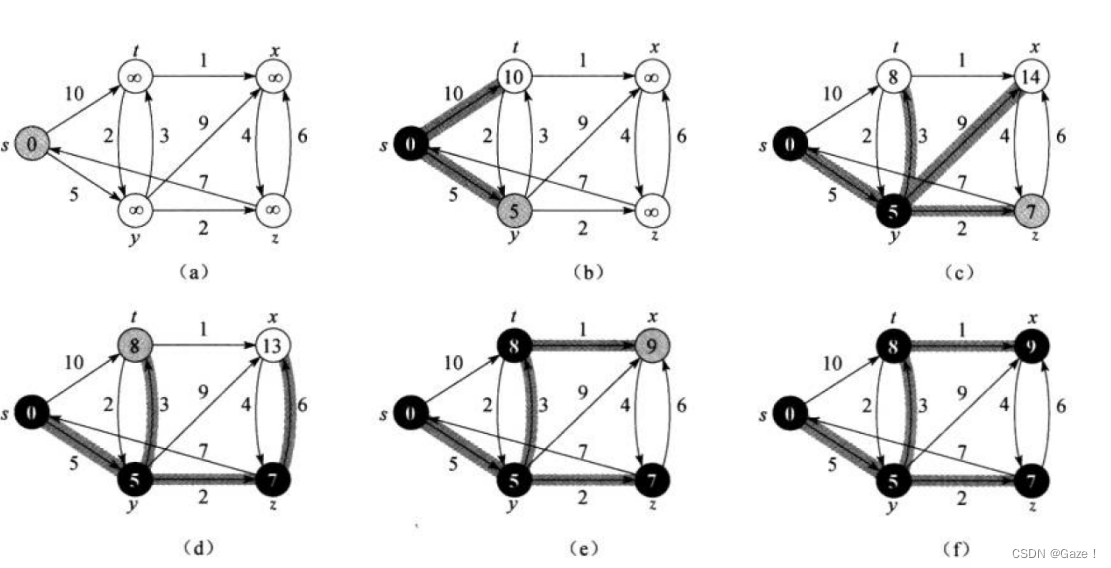
1.1 Dijkstra代码
void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
size_t srci = GetvertexIndex(src);
size_t n = _vertexs.size();
dist.resize(n, MAX_W);
pPath.resize(n, -1);
//将起始顶点到自己的距离置零
dist[srci] = 0;
pPath[srci] = srci;
//S集合 一开始全部未使用
vector<bool> S(n, false);
for (size_t j = 0; j < n; j++)
{
int u = 0;
W min = MAX_W;
for (size_t i = 0; i < n; i++)
{
if (S[i] == false && dist[i] < min)
{
u = i;
min = dist[i];
}
}
//srci->u是最小的边 根据Dijkstra算法 我们把u纳入使用列表
S[u] = true;
//用u来尝试更新dist数组
for (size_t t = 0; t < n; t++)
{
if (S[t] == false && _matrix[u][t]!=MAX_W
&& dist[u] + _matrix[u][t] < dist[t])
{
//从srci到t的权重 大于 从srci到u再从u到t 更新
dist[t] = dist[u] + _matrix[u][t];
pPath[t] = u;//t这个点是从u过来的
}
}
}
}注意是实现在Graph类中的
1.2PrintShortPath函数
在经过Dijkstra算法后的pPath数组是倒着记录路径的,为了方便观察,我们通过一个函数使结果更易观察。
void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath)
{
size_t srci = GetvertexIndex(src);
size_t n = _vertexs.size();
//这里是打印了起始顶点到其他所有顶点的最短路径
for (size_t i = 0; i < n; i++)
{
if (srci != i)
{
int parenti = i;//不能改变i 因为要以i为判据进行循环
vector<int>path;
//所有顶点的起点都是srci 不是就继续找父顶点
while (parenti!= srci)
{
path.push_back(parenti);
parenti = pPath[parenti];
}
//现在父节点就是srci了
path.push_back(srci);
reverse(path.begin(), path.end());
for (auto& e : path)
{
cout << _vertexs[e] << "->";
}
cout << dist[i] << endl;
}
}
}1.3测试代码及结果

注意:Dijkstra无法适用于含有负权边的情况,本质上是贪心思想。负权的介入会影响结果。
2.Bellman-Ford
bellman-ford算法可以解决负权图,但bellman-ford是一种暴力求解的算法,如果是邻接矩阵实现的图才有这种算法,时间复杂度为O(N^3)比Dijkstra算法O(N^2)高。
思路:
其实就是一种暴力遍历。
for (size_t j = 0; j < n; ++j)
{
// srci -> i + i ->j
if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
{
update = true;
cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;
dist[j] = dist[i] + _matrix[i][j];
pPath[j] = i;
}
}
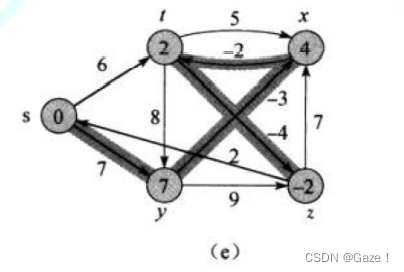
由于是按照顶点的顺序遍历的,当遇到负权的时候,可能会改变路径,但是在此之前的顶点已经按照未改变的路径更新的权值,会造成权值和路径对不上的问题。如下图,syztx的映射为01234,
以s为起始更新,st的权值为6,直到我遍历到i为4(即以x开始更新),此次遍历,让从s->t出现了另一条权值更小的路径(s->y->x->t),但在遍历x之前,s->z的路径是从s->t->z来的,那么s->z本应具有更小的权值,却因为顺序而没有得到调整。
所以我们要进行三次循环遍历。因为新更新路径可能又会影响其他路径,所以还需要继续更新,最多更新n轮。

2.1代码
bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
size_t srci = GetvertexIndex(src);
size_t n = _vertexs.size();
dist.resize(n, MAX_W);
pPath.resize(n, -1);
dist[srci] = 0;// 或者W()更准确
pPath[srci] = srci;//一定要加不然调用PrintShortPath会死循环的
for (size_t k = 0; k < n; k++)
{
bool update = false;
cout << "更新第" << k + 1 << "轮" << endl;
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
{
update = true;
cout << _vertexs[i] << "->" /
<< _vertexs[j] << ":" << _matrix[i][j] << endl;
dist[j] = dist[i] + _matrix[i][j];
pPath[j] = i;
}
}
}
if (update == false)
{
break;
}
}
// 还能更新就是带负权回路
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
// srci -> i + i ->j
if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
{
return false;
}
}
}
return true;
}2.2测试代码及运行结果
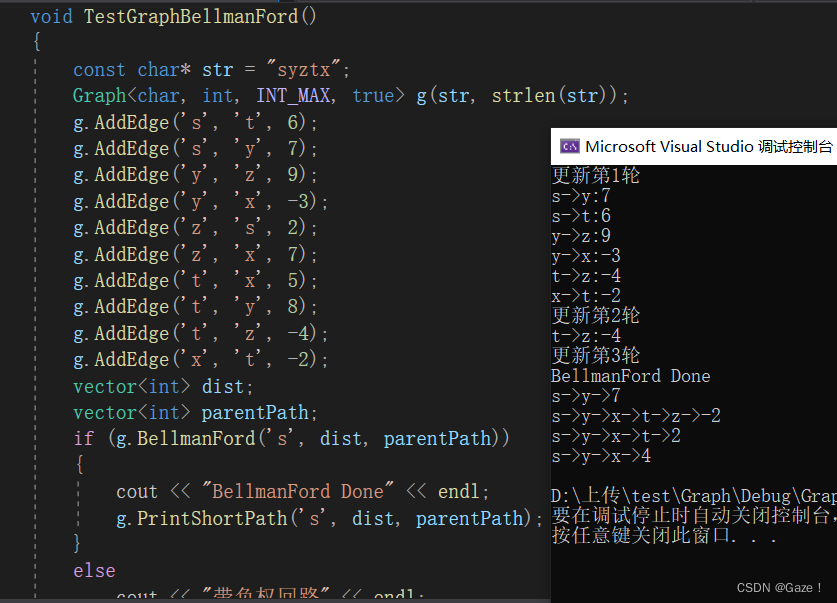
有一个非常奇怪的问题就是我换了个起始节点不是s了,改成'y'就会出现所有路径都是接近INT_MIN的情况。希望有大佬点一点。
3.Floyd-Warshall算法
Floyd-Warshall算法是解决任意两点间的最短路径的一种算法。
Floyd算法考虑的是一条最短路径的中间节点,即简单路径p={v1,v2,…,vn}上除v1和vn的任意节点,设k是p的一个中间节点,那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1,p2。p1 是从i到k且中间节点属于{1,2,…,k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1, 2,…,k-1}取得的一条最短路径。

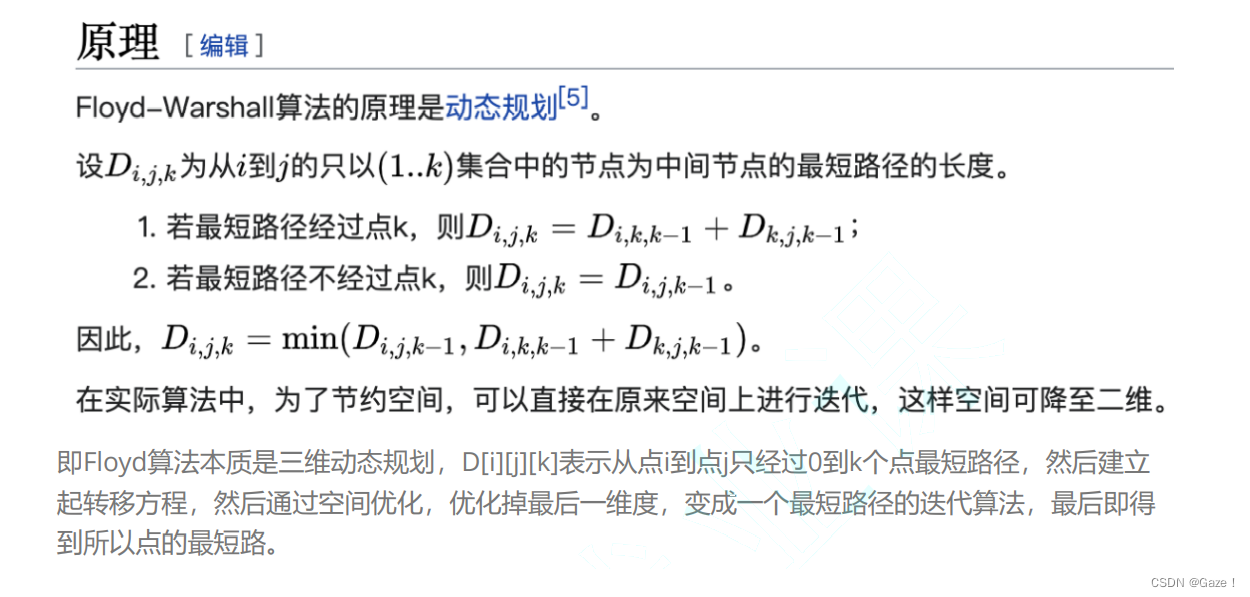
3.1代码
void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{
size_t n = _vertexs.size();
vvDist.resize(n);
vvpPath.resize(n);
for (size_t i = 0; i < n; i++)
{
vvDist[i].resize(n, MAX_W);
vvpPath[i].resize(n, -1);
}
// 直接相连的边更新一下
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
if (_matrix[i][j] != MAX_W)
{
vvDist[i][j] = _matrix[i][j];
vvpPath[i][j] = i;
}
if (i == j)
{
vvDist[i][j] = W();
}
}
}
// abcdef a {} f || b {} c
// 最短路径的更新i-> {其他顶点} ->j
for (size_t k = 0; k < n; ++k)
{
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
// k 作为的中间点尝试去更新i->j的路径
if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W
&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
{
vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
// 找跟j相连的上一个邻接顶点
// 如果k->j 直接相连,上一个点就k,vvpPath[k][j]存就是k
// 如果k->j 没有直接相连,k->...->x->j,vvpPath[k][j]存就是x
vvpPath[i][j] = vvpPath[k][j];
}
}
}
// 打印权值和路径矩阵观察数据
//方便Debug 可以不写
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
if (vvDist[i][j] == MAX_W)
{
printf("%3c", '*');
}
else
{
printf("%3d", vvDist[i][j]);
}
}
cout << endl;
}
cout << endl;
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
printf("%3d", vvpPath[i][j]);
}
cout << endl;
}
cout << "=================================" << endl;
}
}3.2测试代码及结果










![[洛谷]P2234 [HNOI2002]营业额统计](https://img-blog.csdnimg.cn/2b16129baca447e0bbbff25c0fb92c79.png)