目前多准则决策问题的评估方法主要分为定性分析方法和定量分析方法两类。定性分析方法主要包括专家咨询、熵权法、案例研究和德尔菲法等;定量分析法主要包括层次分析法、主成分分析法、因子分析法、模糊综合评价法、色综合评价法以及数据包络分析法(DEA法)、灰云评价等多种方法,不同方法的评价结果都是依据指数或分值对参评对象的综合状况进行排序评价。综合评价方法的选取要依据研究对象的特点而定。
下面以层次分析法为例进行介绍:
层次分析法(The Analytic Hierarchy Process)简记AHP,是美国运筹学家T.L.Satty等人提出的一种定量和定性分析相结合的多准则决策方法,广泛应用于分析复杂的社会、经济以及科学管理领域的问题。其基本原理是通过构造层次分析结构,排列组合得出优劣次序来为决策者提供依据。其特别适合于对无结构特性的系统评价以及多目标、多准则、多时期等的系统评价。目前已经在大气环境研究、水环境研究、生态环境研究等领域得到了广泛应用。
层次分析法的一般步骤:
(1)建立目标层次结构。该层次结构模型由从上至下目标层、准则层、指标层组成。各层之间,上层受下层影响,而层内互相独立。
(2)构建判断矩阵。决策者按照下层评价因子对上层因子的重要程度,分别对准则层因素和指标层评价因子进行两两对比分析,构造准则层相对一目标层、指标层相对于准则层各单因素的判断矩阵。具体如下:
依次对同一层次中归属于同一上层准则的两两元素的重要程度进行对比分析,建立判断矩阵 ,矩阵具有以下性质aij>0,
,矩阵具有以下性质aij>0,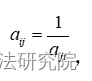 ,aij=(i,j=1,2,…n)。式中表示元素 和关于上一层次重要程度的比较结果,通常采用1~9 比例标度法来对重要程度进行赋值,1 表示同等重要,9 表示前者重要程度远超后者;反之相应的倒数表示不重要程度,如1/9 表示前者重要程度远远不及后者。
,aij=(i,j=1,2,…n)。式中表示元素 和关于上一层次重要程度的比较结果,通常采用1~9 比例标度法来对重要程度进行赋值,1 表示同等重要,9 表示前者重要程度远超后者;反之相应的倒数表示不重要程度,如1/9 表示前者重要程度远远不及后者。
根据获得的判断矩阵A,计算其最大特征根![]() ,相应的特征向量W,进行归一化处置的W 向量也就是同一层级元素相互之间的权重比例。
,相应的特征向量W,进行归一化处置的W 向量也就是同一层级元素相互之间的权重比例。

由于被评价对象复杂以及评价者思维逻辑的多样与局限,判断矩阵有一定概率会出现“甲的重要性高于乙,乙的重要性又高于丙,但丙的重要性反而比甲高”的逻辑矛盾导致结果不合理,因此必须针对判断矩阵开展一致性检验,具体检验方法如下:

表4-5 平均随机一致性指标表
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.00 | 0.00 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
注:根据随机一致性比率C.R.的含义,当矩阵为一阶或者二阶时,C.R.一定为0,因此矩阵为一阶或者二阶时一定通过一致性检验,只需要计算出特征向量作为权重系数即可。
(4)确定各指标的综合权重。
基于层次分析法,对于定量化每个指标在层次结构中对于上一层因素的影响,萨蒂提出了“1-9”比较标度法。每位专家将依据此对于每个层次中的各个指标对于其他指标的重要性分别按照1、3、5、7、9进行打分,每个分数的具体含义见表1。在打分中,倒数代表相反的重要性含义。
表 1 比较标度代表含义
| 比较标度 | 代表含义 |
| 1 | 两者重要性相同 |
| 3 | 比后者稍微重要 |
| 5 | 比后者较强重要 |
| 7 | 比后者强烈重要 |
| 9 | 比后者极端重要 |
案例实现代码如下: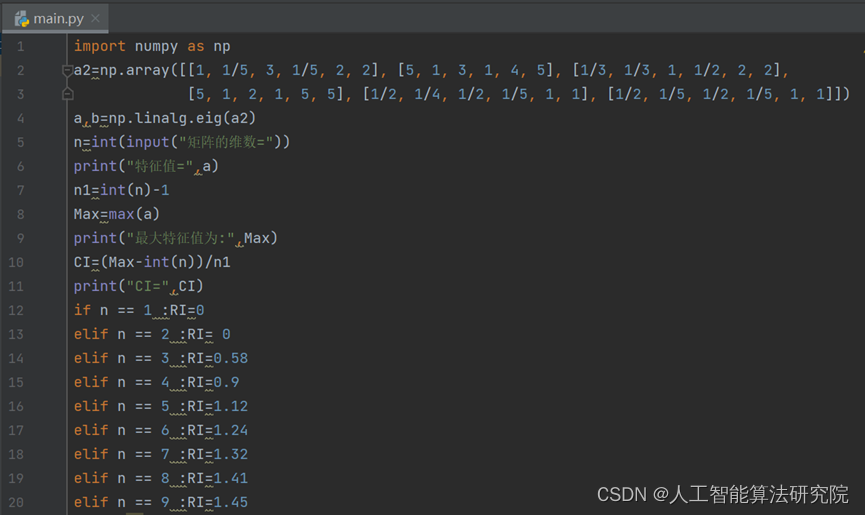



![[FireshellCTF2020]Caas](https://img-blog.csdnimg.cn/a8cca0273f514933a612d556de0ac0eb.png)