概念
图是由顶点和边组成的一种数据结构,我们之前介绍的树形结构中,树的每一个节点就是顶点,顶点与顶点中的连线就是边,也就是说,树是一种特殊的图
图中的边如果有方向,那么这个图就称为有向图,反之则成为无向图
完全图
如果一个无向图中任意两个节点之间有且仅有一条边,那么称这个图为无向完全图,而一个有向图中,任意两个节点间有且仅有方向相反的边,称之为有向完全图
下图中左侧为无向完全图,右侧为有向完全图
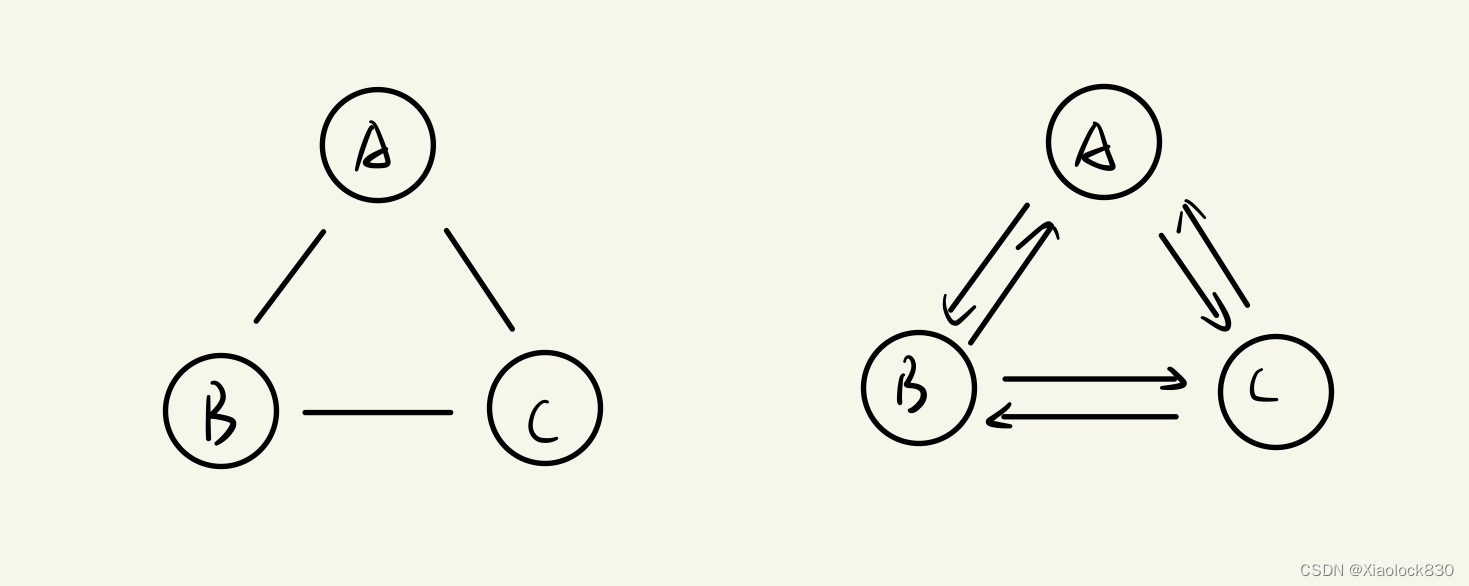
顶点的度
指的是有几条边与该节点关联,如果是完全图的话,那么分为入度和出度,箭头指向该节点的是这个节点的入度,反之为出度
下图中左侧的所有节点的度都是2,右侧所有节点的入度都是2,出度都是2,也即是所有节点的度都是4
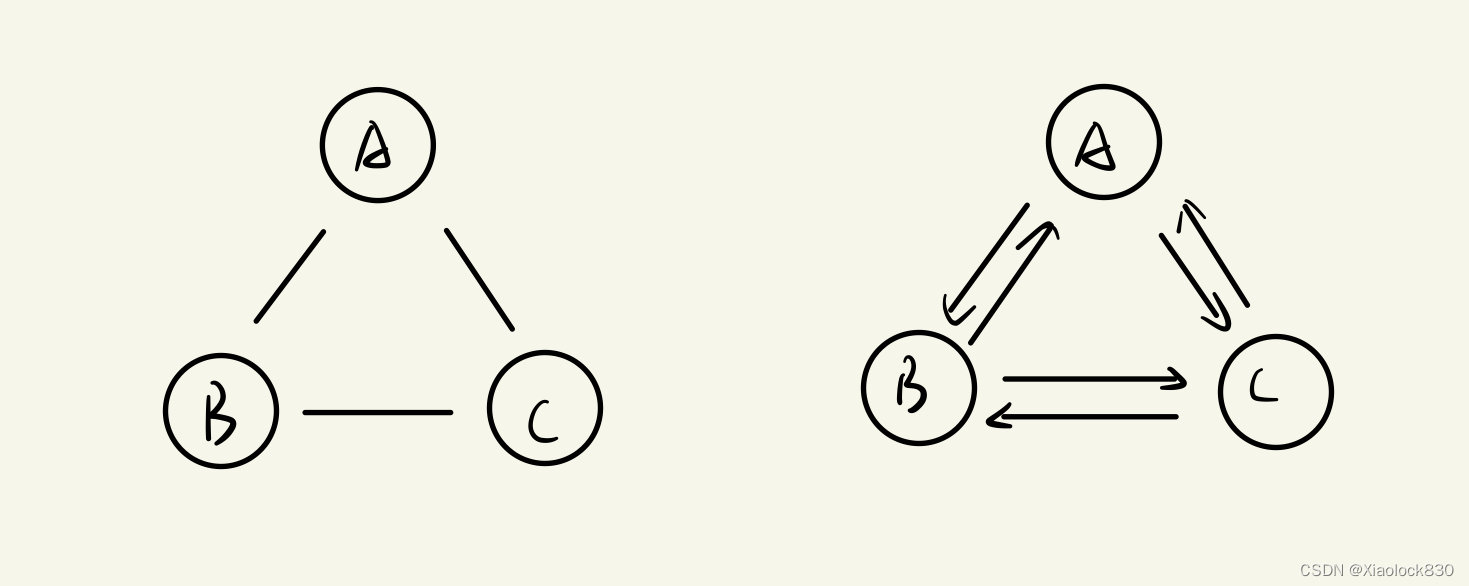
路径
一个节点到另一个节点要走的边称之为路径,如果这些边上有权值(例如一个节点是北京,一个是天津,一个是上海,那么北京到天津的权值和北京到上海的权值是不一样的)
对于无向图,两个节点间的路径长度等于边的个数
对于有向图,两个节点间的路径长度等于所有边的权值之和
回路和环
对于一个路径,如果起点和终点都一样,那么称这个路径为回路,而如果这个路径的长度为一,也就是这个边是自己指向自己,称之为环
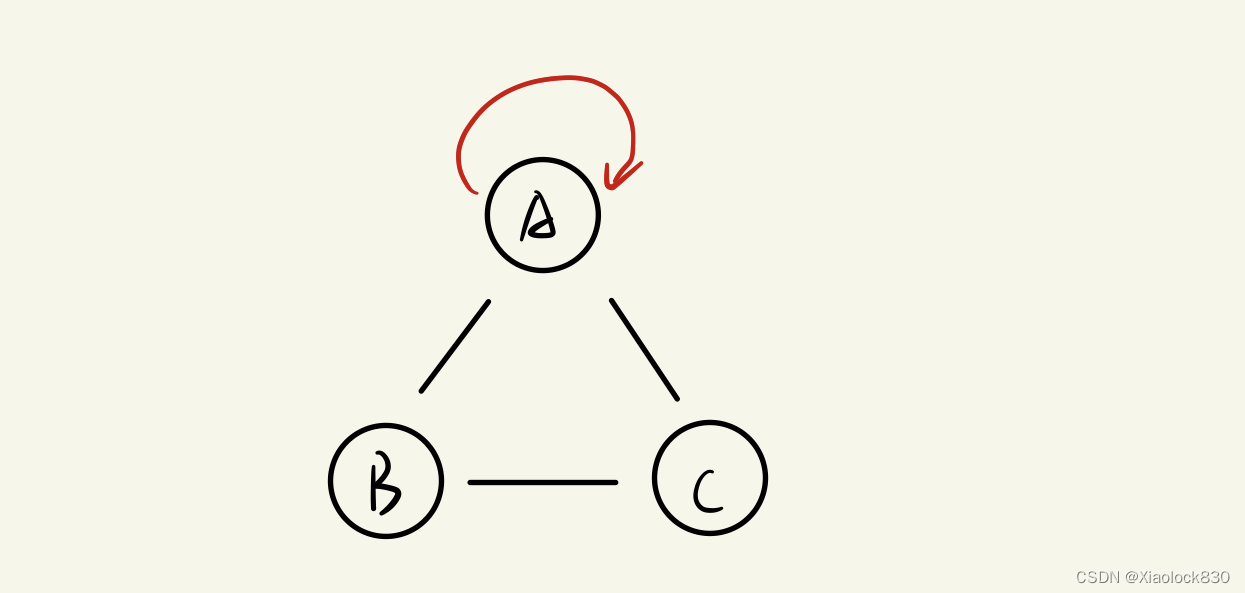
上图中黑色的三条边组成回路,红色的是环
子图
对于图G,如果图G1的节点都属于图G,边都属于图G,则称G1为G的子图
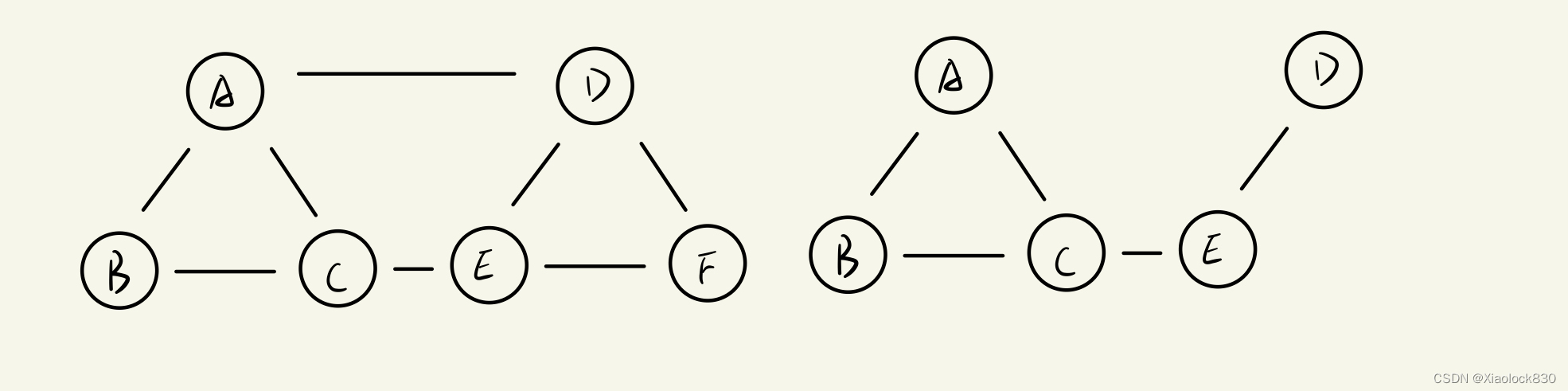
例如上图,右面的图就是左侧的图的子图
连通图
如果无向图中任意两个节点间都是有一条路径的,则称这个图是连通图
如果有向图中任意两个节点间都是有一条从起始点到终止点的路径,还有一条从终止点到起始点的路径,则称这个图是强连通图
一个连通图的最小连通子图是该图的生成树
图的存储
在计算机中,主要有下面两种方法来存储图
邻接矩阵
使用矩阵(二维数组来存储节点与节点之间的关系)
对于无向图,两个节点之间如果有边,就是1,或者是边的权值,没有就是0,自己和自己是0,因此,无向图的邻接矩阵表示是关于对角线对称的
对于有向图,一个节点如果有指向另一个节点的边,就是1或者是边的权值,否则就是正无穷,自己和自己是0
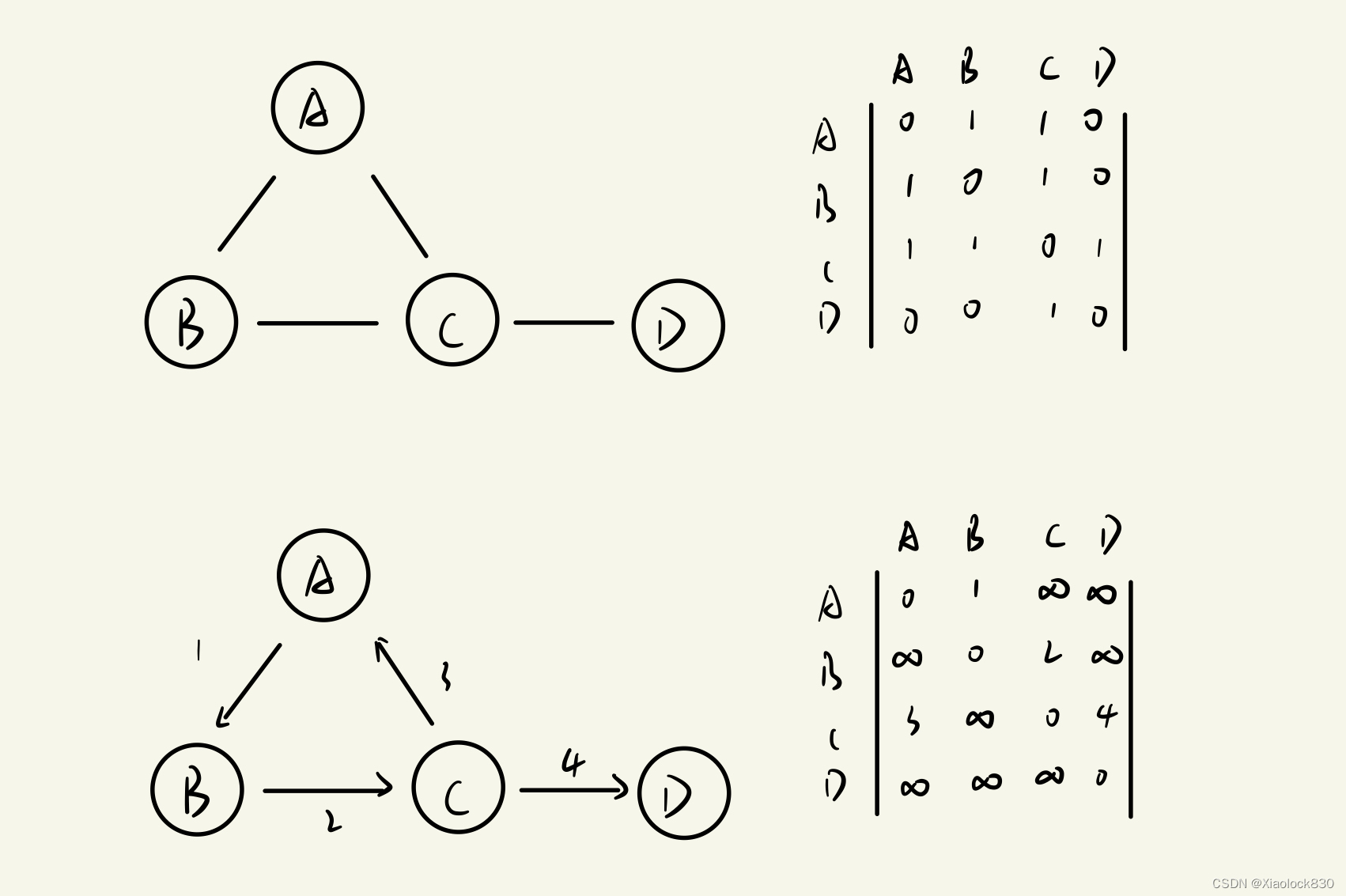
代码实现
定义一个最大值代表正无穷
public class Constant {
public static final int MAX = Integer.MAX_VALUE;
}
import java.util.Arrays;
/**
* 使用邻接矩阵存储图
*/
public class GraphByMatrix {
private char[] arrayV;//顶点数组
private int[][] matrix;//邻接矩阵
private boolean isDirect;//是否为有向图
/**
* @param size 当前矩阵的顶点个数
* @param isDirect
*/
public GraphByMatrix(int size, boolean isDirect){
this.arrayV = new char[size];
matrix = new int[size][size];
for (int i = 0; i < size; i++) {
Arrays.fill(matrix[i],Constant.MAX);
}
this.isDirect = isDirect;
}
/**
* 初始化顶点数组
* @param array
*/
public void initArrayV(char[] array){
for (int i = 0; i < arrayV.length; i++) {
arrayV[i] = array[i];
}
}
/**
* 添加边
* @param srcV 起点
* @param destV 终点
* @param weight 权值
*/
public void addEdge(char srcV, char destV, int weight){
int srcIndex = getIndexOfV(srcV);
int destIndex = getIndexOfV(destV);
matrix[srcIndex][destIndex] = weight;
//无向图的对称位置也有对应的权值
if(!isDirect){
matrix[destIndex][srcIndex] = weight;
}
}
/**
* 获取v顶点的下标
* @param v
* @return
*/
private int getIndexOfV(char v){
for (int i = 0; i < arrayV.length; i++) {
if (arrayV[i] == v){
return i;
}
}
return -1;
}
/**
* 获取顶点的度
* 有向图为入度+出度
* @param v
* @return
*/
public int getDevOfV(char v){
int count = 0;
int srcIndex = getIndexOfV(v);
//计算出度
for (int i = 0; i < arrayV.length; i++) {
if(matrix[srcIndex][i] != Constant.MAX){
count++;
}
}
//计算入度
if(isDirect){
for (int i = 0; i < arrayV.length; i++) {
if(matrix[i][srcIndex] != Constant.MAX){
count++;
}
}
}
return count;
}
private void printGraph() {
for (int i = 0; i < arrayV.length; i++) {
System.out.print(arrayV[i] + " ");
}
System.out.println();
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
if(matrix[i][j] == Constant.MAX){
System.out.print("∞ ");
} else {
System.out.print(matrix[i][j] + " ");
}
}
System.out.println();
}
}
public static void main(String[] args) {
GraphByMatrix graph = new GraphByMatrix(4,true);
char[] array = {'A','B','C','D'};
graph.initArrayV(array);
graph.addEdge('A','B',1);
graph.addEdge('A','D',1);
graph.addEdge('B','A',1);
graph.addEdge('B','C',1);
graph.addEdge('C','B',1);
graph.addEdge('C','D',1);
graph.addEdge('D','A',1);
graph.addEdge('D','C',1);
graph.printGraph();
System.out.println(graph.getDevOfV('A'));
}
}
邻接表
使用数组来表示顶点的集合,使用链表来表示边的关系
也就是说,每一个链表中存储了目标顶点所在的下标
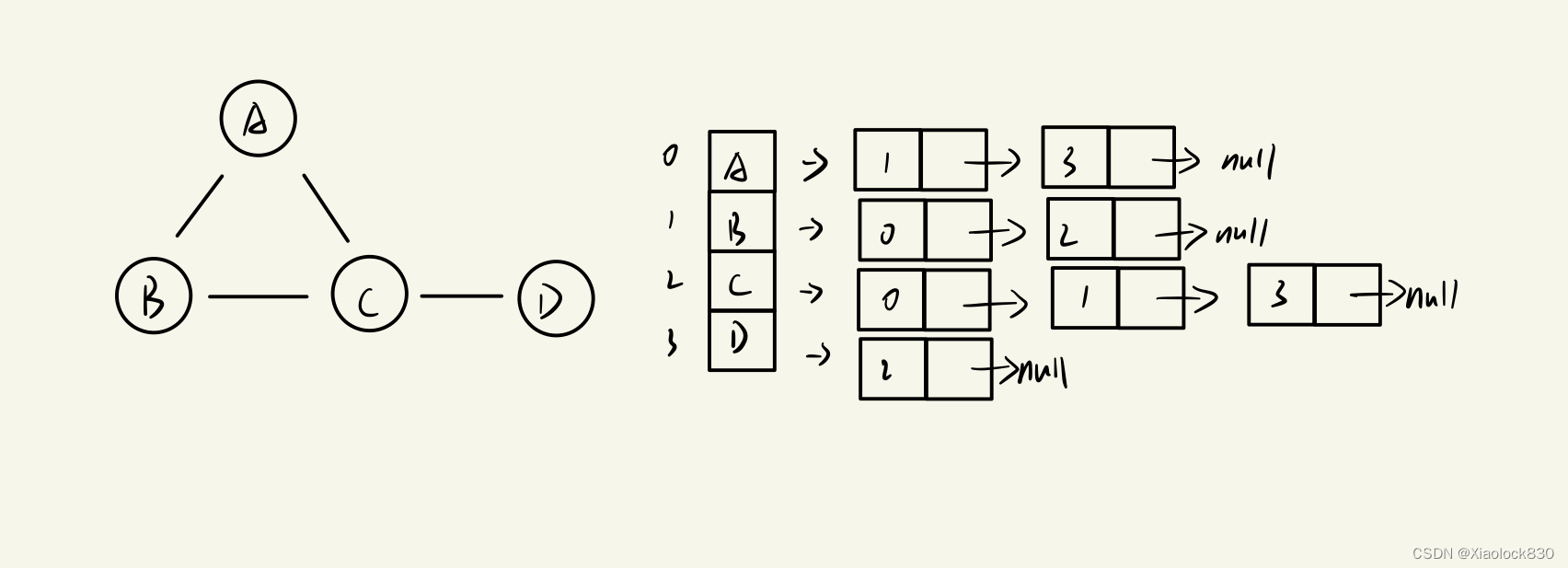
而如果是有向图,那么会存储两个表,一个是入边表,另一个则是出边表
代码实现
import java.util.ArrayList;
/**
* 使用邻接表存储图
*/
public class GraphByNode {
static class Node{
public int src;//起始位置
public int dest;//目标位置
public int weight;//权重
public Node next;
public Node(int src, int dest, int weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
}
public char[] arrayV;//存储顶点
public ArrayList<Node> edgList;//存储边
public boolean isDirect;
public GraphByNode(int size, boolean isDirect){
this.arrayV = new char[size];
edgList = new ArrayList<>(size);
for (int i = 0; i < size; i++) {
edgList.add(null);
}
this.isDirect = isDirect;
}
/**
* 初始化顶点数组
* @param array
*/
public void initArrayV(char[] array){
for (int i = 0; i < arrayV.length; i++) {
arrayV[i] = array[i];
}
}
/**
* 添加边
* @param srcV
* @param destV
* @param weight
*/
public void addEdge(char srcV, char destV, int weight){
int srcIndex = getIndexOfV(srcV);
int destIndex = getIndexOfV(destV);
addEdgeChild(srcIndex,destIndex,weight);
if(!isDirect){
addEdgeChild(destIndex,srcIndex,weight);
}
}
private void addEdgeChild(int srcIndex, int destIndex, int weight){
Node cur = edgList.get(srcIndex);
while(cur != null){
if(cur.dest == destIndex){
return;
}
cur = cur.next;
}
//之前没有存储过这条边
//头插法
Node node = new Node(srcIndex,destIndex,weight);
node.next = edgList.get(srcIndex);
edgList.set(srcIndex,node);
}
/**
* 获取v顶点的下标
* @param v
* @return
*/
private int getIndexOfV(char v){
for (int i = 0; i < arrayV.length; i++) {
if (arrayV[i] == v){
return i;
}
}
return -1;
}
/**
* 获取顶点的度
* @param v
* @return
*/
public int getDevOfV(char v){
int count = 0;
int srcIndex = getIndexOfV(v);
Node cur = edgList.get(srcIndex);
while(cur != null){
count++;
cur = cur.next;
}
if(isDirect){
int destIndex = srcIndex;
for (int i = 0; i < arrayV.length; i++) {
if(i == destIndex){
continue;
} else {
Node pCur = edgList.get(i);
while(pCur != null){
if(pCur.dest == destIndex){
count++;
}
pCur = pCur.next;
}
}
}
}
return count;
}
public void printGraph(){
for (int i = 0; i < arrayV.length; i++) {
System.out.println(arrayV[i] + " ->");
Node cur = edgList.get(i);
while(cur != null){
System.out.print(arrayV[cur.dest] + " ->");
cur = cur.next;
}
System.out.println();
}
}
public static void main(String[] args) {
GraphByNode graph = new GraphByNode(4,true);
char[] array = {'A','B','C','D'};
graph.initArrayV(array);
graph.addEdge('A','B',1);
graph.addEdge('A','D',1);
graph.addEdge('B','A',1);
graph.addEdge('B','C',1);
graph.addEdge('C','B',1);
graph.addEdge('C','D',1);
graph.addEdge('D','A',1);
graph.addEdge('D','C',1);
graph.printGraph();
System.out.println(graph.getDevOfV('A'));
}
}