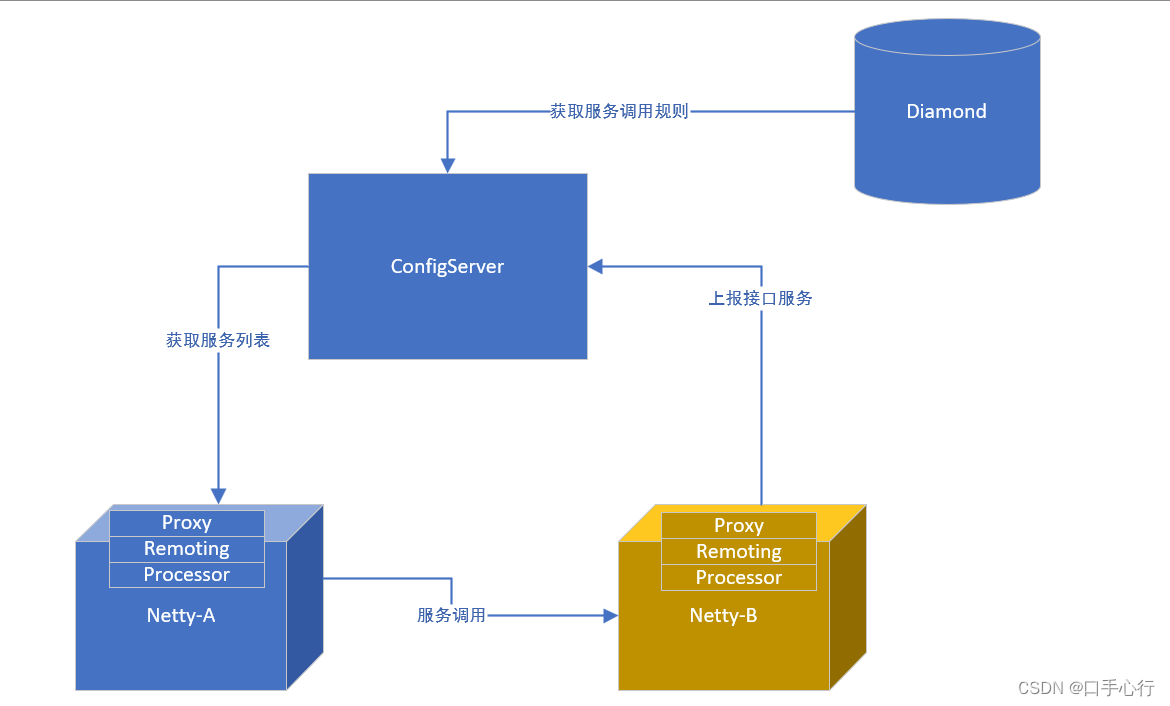
谱分析介绍
谱分析是一种用于研究函数的数学方法。在数学中,谱分析的基本概念是将函数分解成不同的频率成分,以便更好地理解其行为。这些频率成分可以表示为正弦或余弦函数的级数和,称为谱线。
谱分析常用于信号处理、音频信息处理和图像处理等领域。常用的谱分析方法包括傅里叶变换、小波变换和短时傅里叶变换等。
例如,在音频信息处理中,谱分析可用于将音频信号分解成不同的频率成分,以便更好地理解其各种声音的组成。在图像处理中,谱分析可用于将图像信息分解成不同的频率成分,以便更好地理解图像中各种纹理的组成。
Matlab 实现功率谱
在 Matlab 中,可以使用函数 pwelch 来实现功率谱的计算。
该函数的用法如下
[Pxx,f] = pwelch(x)
其中 x 是需要计算功率谱的信号,Pxx 是计算得到的功率谱,f 是频率轴。
例如,假设有一个信号 x,可以使用以下代码来计算它的功率谱:
[Pxx,f] = pwelch(x);
plot(f,Pxx);
这将绘制出功率谱的图像,其中横坐标为频率,纵坐标为功率。
需要注意的是,pwelch 函数默认使用汉宁窗进行加窗,并使用默认的参数计算功率谱。如果需要更改窗函数或其他参数,可以使用函数的其他可选参数进行调整。可以参考 Matlab 帮助文档了解更多关于 pwelch 函数的使用方法。
matlab 实现功率谱的例子
以下是一个使用 Matlab 实现功率谱的例子:
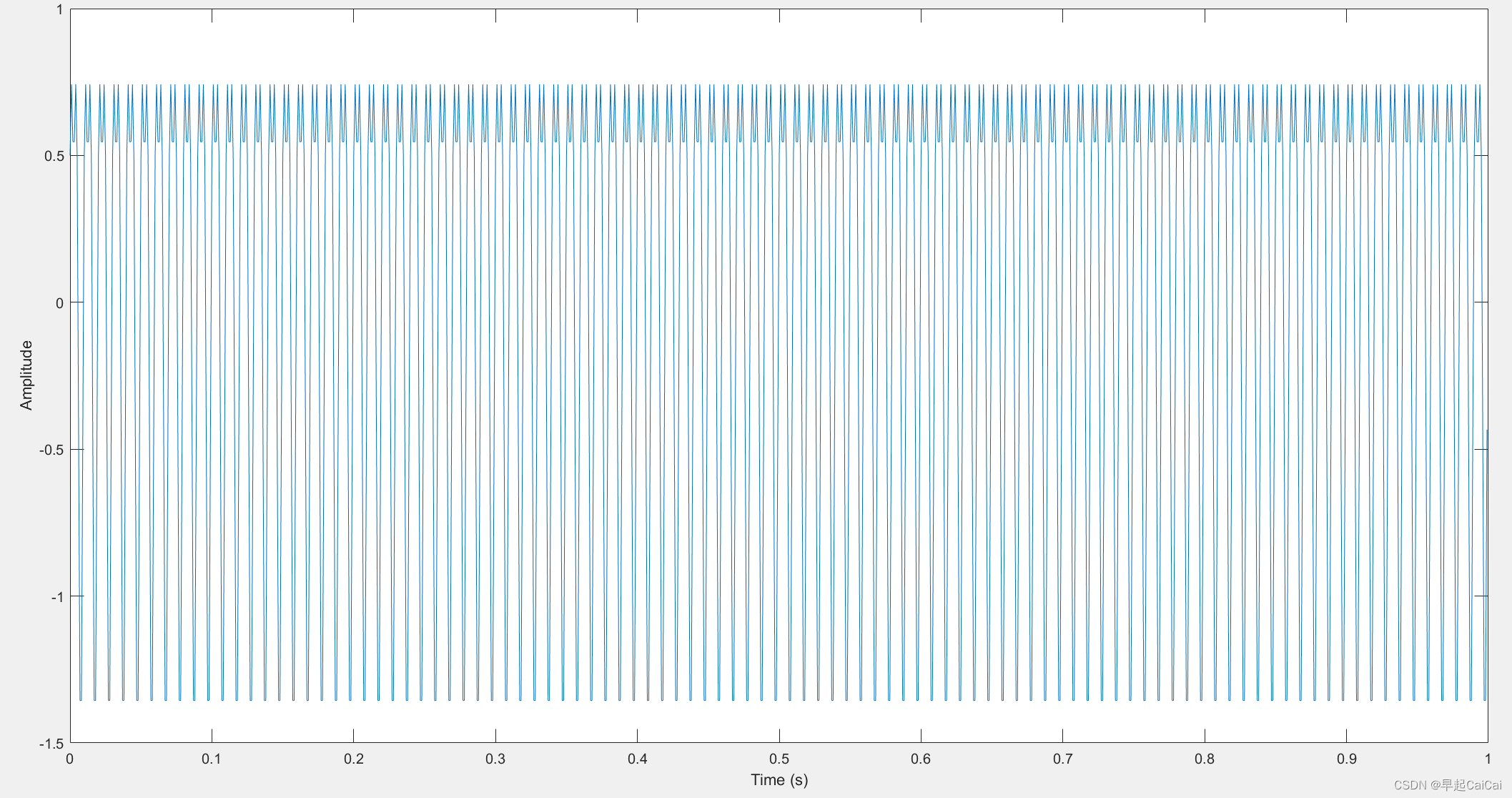
首先,假设有一个信号 x,它的采样频率为 1000 Hz,信号长度为 1000 个点。我们可以使用如下代码来生成信号并绘制出它的时域波形:
Fs = 1000; % 采样频率
t = 0:1/Fs:1-1/Fs; % 采样时间
x = sin(2*pi*100*t) + 0.5*cos(2*pi*200*t); % 生成信号
figure; % 打开新的图像窗口
plot(t,x); % 绘制信号的时域波形
xlabel('Time (s)'); % 设置 x 轴标签
ylabel('Amplitude'); % 设置 y 轴标签
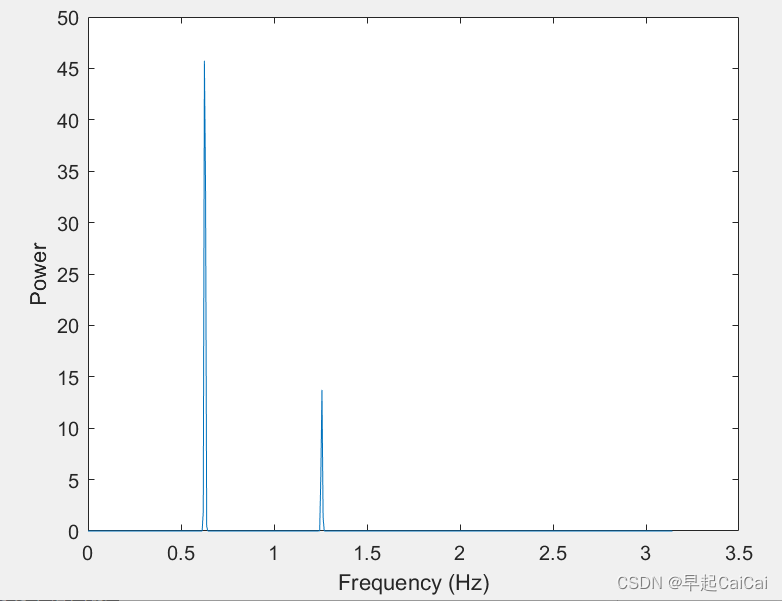
然后,我们可以使用 pwelch 函数来计算信号的功率谱:
[Pxx,f] = pwelch(x,Fs); % 计算功率谱
figure; % 打开新的图像窗口
plot(f,Pxx); % 绘制功率谱图像
xlabel('Frequency (Hz)'); % 设置 x 轴标签
ylabel('Power'); % 设置 y 轴标签
这将绘制出信号的功率谱图像,其中横坐标为频率,纵坐标为功率。
功率谱的单位问题
功率谱是描述信号中频率分量的强度的一种方法。它可以用来分析信号的频谱分布,了解信号中不同频率成分的相对强度。
功率谱的单位取决于信号的原单位。通常情况下,功率谱的单位为信号原单位的平方,例如,如果信号的原单位是伏特(V),则功率谱的单位为伏特平方(V^2)。
但是,在某些情况下,功率谱的单位可能并不是信号原单位的平方。例如,如果信号的原单位是功率(W),则功率谱的单位为功率(W)。
对于时域信号,可以使用功率谱密度(Power Spectral Density,PSD)来表示功率谱。功率谱密度的单位通常为信号原单位的平方,除以频率单位。
例如,假设有一个时域信号,其原单位为伏特(V),频率单位为赫兹(Hz)。则该信号的功率谱单位为伏特平方(V^2)/赫兹(Hz)。
如果使用功率谱密度(Power Spectral Density,PSD)来表示时域信号的功率谱,则功率谱密度的单位为信号原单位的平方,除以频率单位的平方。例如,假设有一个时域信号,其原单位为伏特(V),频率单位为赫兹(Hz)。则该信号的功率谱密度单位为伏特平方(V2次方)/赫兹平方(Hz^2)。
对于时域信号的功率谱,还有一些其他的常用单位,例如分贝(dB)和帕斯卡(Pa)。
分贝(dB)是一种相对单位,表示信号强度与某个参考信号强度之间的差值。分贝单位是基于对数关系定义的,公式为:
d
B
=
10
log
10
(
P
P
r
e
f
)
dB = 10\log_{10}\left(\frac{P}{P_{ref}}\right)
dB=10log10(PrefP)
其中,
P
P
P 表示信号的功率,
P
r
e
f
P_{ref}
Pref 表示参考信号的功率。
因此,分贝单位下的功率谱单位为信号的功率与参考信号的功率之比的对数。
例如,假设有一个时域信号,其原单位为伏特(V),频率单位为赫兹(Hz)。则该信号的功率谱单位为伏特平方(V^2)/赫兹(Hz),与参考信号的功率之比的对数(单位为分贝)。
如果使用功率谱密度(Power Spectral Density,PSD)来表示时域信号的功率谱,则功率谱密度的单位为伏特平方( V 2 V^2 V2)/赫兹平方(Hz^2),与参考信号的功率之比的对数(单位为分贝)。
帕斯卡(Pa)是一种常用的功率谱单位,常用于声学信号的功率谱。帕斯卡单位系统的定义是:1帕斯卡(Pa)= 1 N/m^2。其中,N 表示牛(Newton),m 表示米(meter)。
因此,帕斯卡单位系统下的功率谱单位为牛平方(N的2次方)/米平方(m^2)。
例如,假设有一个时域信号,其原单位为帕斯卡(Pa),频率单位为赫兹(Hz)。则该信号的功率谱单位为牛平方(N的2次方)/米平方(m^2)/赫兹(Hz)。
如果使用功率谱密度(Power Spectral Density,PSD)来表示时域信号的功率谱,则功率谱密度的单位为牛平方( N 2 N^2 N2)/米平方( m 2 m^2 m2)/赫兹平方(Hz^2)。
较为复杂的功率谱问题
案例1(直接法)
clc
clear;
Fs=1000; %采样频率
n=0:1/Fs:1;
%产生含有噪声的序列
xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));
window=boxcar(length(xn)); %矩形窗
nfft=1024;
[Pxx,f]=periodogram(xn,window,nfft,Fs); %直接法
plot(f,10*log10(Pxx));
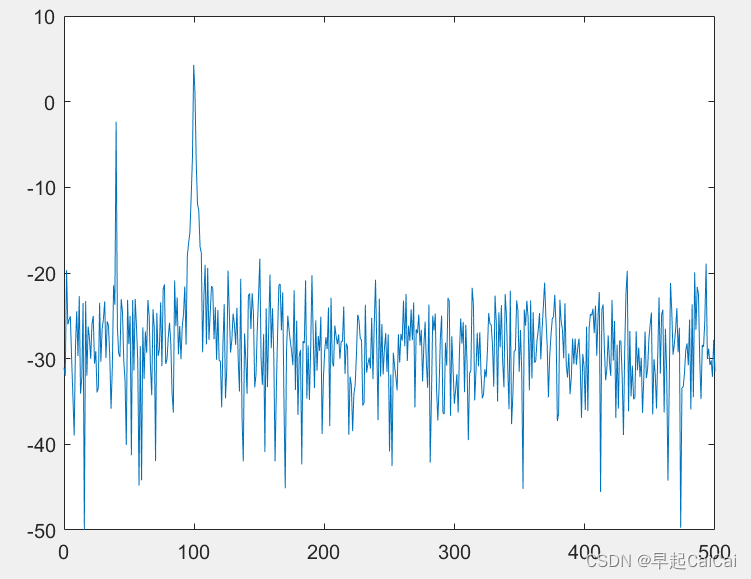
这段代码是用来计算时域信号的功率谱的。
具体地,这段代码首先定义了采样频率 F s Fs Fs,并使用这个采样频率产生了一个含有噪声的时域信号序列 x n xn xn。然后使用矩形窗函数产生了一个矩形窗,并使用 periodogram 函数计算了时域信号的功率谱。最后,使用 plot 函数绘制了时域信号的功率谱图。
注意,periodogram 函数返回的功率谱是以伏特平方(V^2)为单位的,因此在绘制功率谱图时使用了 10*log10 函数将功率谱转换成分贝单位。
间接法去求
间接法先由序列x(n)估计出自相关函数R(n),然后对R(n)进行傅立叶变换,便得到x(n)的功率谱估计。
clear;
Fs=1000; %采样频率
n=0:1/Fs:1;
%产生含有噪声的序列
xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));
nfft=1024;
cxn=xcorr(xn,'unbiased'); %计算序列的自相关函数
CXk=fft(cxn,nfft);
Pxx=abs(CXk);
index=0:round(nfft/2-1);
k=index*Fs/nfft;
plot_Pxx=10*log10(Pxx(index+1));
plot(k,plot_Pxx);
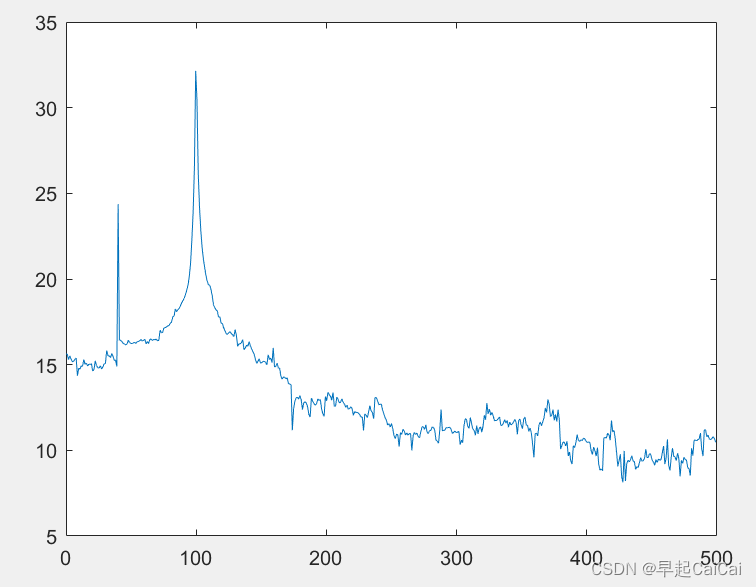
这段代码首先定义了采样频率 F s Fs Fs,并使用这个采样频率产生了一个含有噪声的时域信号序列 x n xn xn。然后使用 xcorr 函数计算了时域信号的自相关函数,并使用 fft 函数计算了其频域表示。最后,使用 plot 函数绘制了时域信号的功率谱图。
注意,自相关函数的频域表示就是时域信号的功率谱。因此在计算功率谱时,可以直接使用 fft 函数计算自相关函数的频域表示。此外,自相关函数的频域表示也是以伏特平方(V^2)为单位的,因此在绘制功率谱图时使用了 10*log10 函数将功率转化为dB。
案例3(改进的直接法):Bartlett法
对于直接法的功率谱估计,当数据长度N太大时,谱曲线起伏加剧,若N太小,谱的分辨率又不好,因此需要改进。
Bartlett平均周期图的方法是将N点的有限长序列x(n)分段求周期图再平均。
clear;
Fs=1000;
n=0:1/Fs:1;
xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));
nfft=1024;
window=boxcar(length(n)); %矩形窗
noverlap=0; %数据无重叠
p=0.9; %置信概率
[Pxx,Pxxc]=psd(xn,nfft,Fs,window,noverlap,p);
index=0:round(nfft/2-1);
k=index*Fs/nfft;
plot_Pxx=10*log10(Pxx(index+1));
plot_Pxxc=10*log10(Pxxc(index+1));
figure(1)
plot(k,plot_Pxx);
pause;
figure(2)
plot(k,[plot_Pxx plot_Pxx-plot_Pxxc plot_Pxx+plot_Pxxc]);
这段代码首先定义了采样频率 F s Fs Fs,并使用这个采样频率产生了一个含有噪声的时域信号序列 x n xn xn。然后使用矩形窗函数产生了一个矩形窗,并使用 psd 函数计算了时域信号的功率谱及其置信区间。最后,使用 plot 函数绘制了时域信号的功率谱图。
psd 函数返回的功率谱是以伏特平方(V^2)为单位的,因此在绘制功率谱图时使用了 10*log10 函数将功率谱转换成分贝单位。此外,psd 函数还返回了置信区间,即功率谱的置信区间边界。在绘制功率谱图时,可以将功率谱和置信区间边界一起绘制在同一个图上,以展示功率谱的不确定性。
注意,在这段代码中,使用了 figure 函数分别在两个图窗中绘制功率谱图。另外,使用了 pause 函数来停顿代码的执行,以便在两个图窗中分别查看功率谱图。
在最新版的 MATLAB 中,psd 函数已被弃用。如果要计算时域信号的功率谱,可以使用 periodogram 函数或 pwelch 函数。
下面是将上述代码改用 periodogram 函数的例子
clear;
Fs=1000;
n=0:1/Fs:1;
xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));
nfft=1024;
window=boxcar(length(n)); %矩形窗
[Pxx,f]=periodogram(xn,window,nfft,Fs); %计算功率谱
index=0:round(nfft/2-1);
plot_Pxx=10*log10(Pxx(index+1));
plot(f(index+1),plot_Pxx);
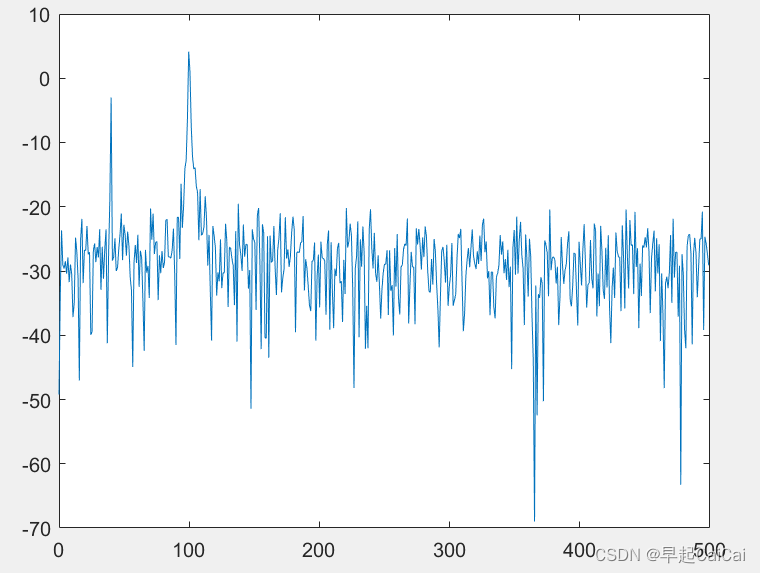
下面是将上述代码改用 pwelch 函数的例子:
clear;
Fs=1000;
n=0:1/Fs:1;
xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));
nfft=1024;
window=boxcar(length(n)); %矩形窗
noverlap=0; %数据无重叠
[Pxx,f]=pwelch(xn,window,noverlap,nfft,Fs); %计算功率谱
index=0:round(nfft/2-1);
plot_Pxx=10*log10(Pxx(index+1));
plot(f(index+1),plot_Pxx);
注意,在使用 pwelch 函数时,需要指定窗函数、数据重叠的量和功率谱的 FFT 长度。此外,pwelch 函数还可以计算功率谱的置信区间,但需要使用不同的参数。
如果要计算功率谱的置信区间,可以使用 pwelch 函数的’ConfidenceLevel’参数指定置信水平。例如,计算 90% 置信水平的置信区间,可以使用如下代码:
[Pxx,f,Pxxc]=pwelch(xn,window,noverlap,nfft,Fs,'ConfidenceLevel',0.9);
最后,注意 periodogram 函数和 pwelch 函数的返回值有所不同。periodogram 函数返回功率谱和频率数组,而 pwelch 函数返回功率谱、频率数组和置信区间边界。因此,在使用 periodogram 和 pwelch 函数时,需要根据返回值的不同进行相应的处理。
案例4(改进的直接法):Welch法
Welch法对Bartlett法进行了两方面的修正,一是选择适当的窗函数w(n),并再周期图计算前直接加进去,加窗的优点是无论什么样的窗函数均可使谱估计非负。二是在分段时,可使各段之间有重叠,这样会使方差减小。
clear;
Fs=1000;
n=0:1/Fs:1;
xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));
nfft=1024;
window=boxcar(100); %矩形窗
window1=hamming(100); %海明窗
window2=blackman(100); %blackman窗
noverlap=20; %数据无重叠
range='half'; %频率间隔为[0 Fs/2],只计算一半的频率
[Pxx,f]=pwelch(xn,window,noverlap,nfft,Fs,range);
[Pxx1,f]=pwelch(xn,window1,noverlap,nfft,Fs,range);
[Pxx2,f]=pwelch(xn,window2,noverlap,nfft,Fs,range);
plot_Pxx=10*log10(Pxx);
plot_Pxx1=10*log10(Pxx1);
plot_Pxx2=10*log10(Pxx2);
figure(1)
plot(f,plot_Pxx);
pause;
figure(2)
plot(f,plot_Pxx1);
pause;
figure(3)
plot(f,plot_Pxx2);
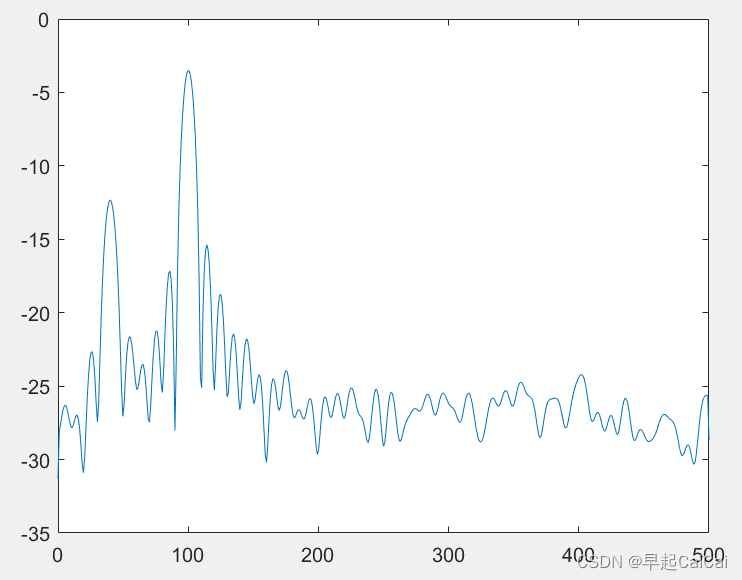
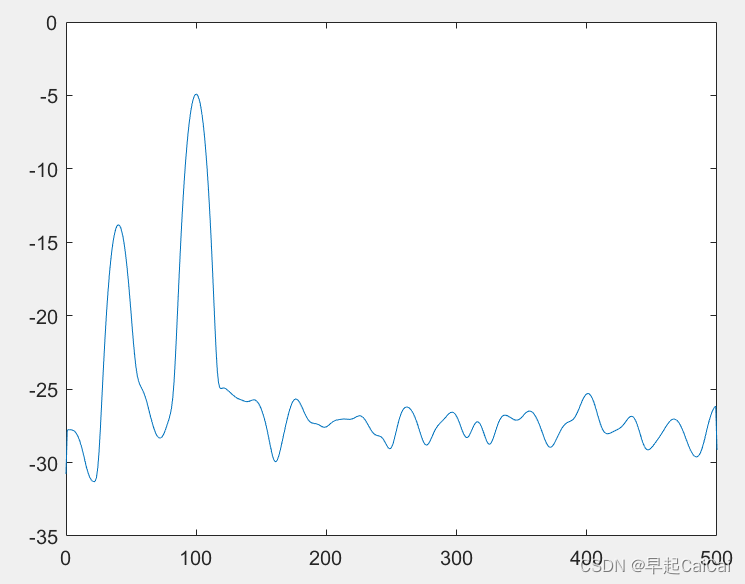
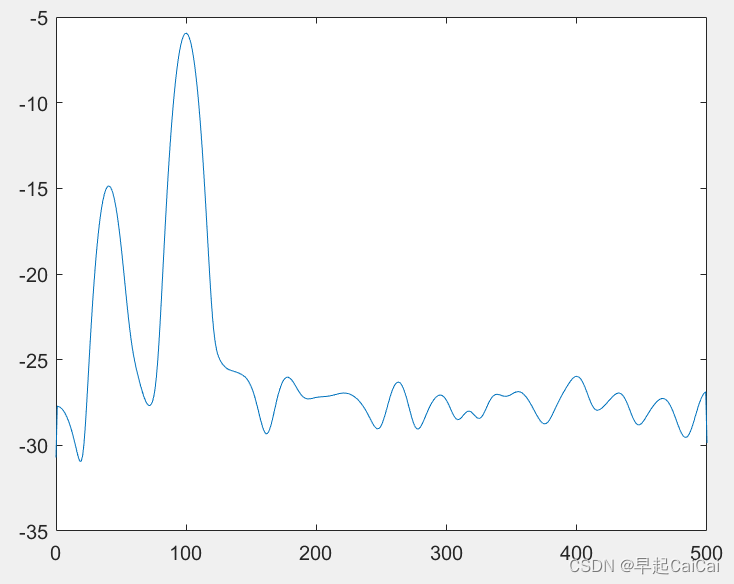
在上述代码中,使用了三种窗函数:矩形窗(boxcar)、海明窗(hamming)和 Blackman 窗(blackman)。使用这三种窗函数分别计算了信号的功率谱,并使用 pwelch 函数绘制了功率谱的曲线。
在使用窗函数时,需要注意窗函数的长度和数据重叠的量。通常情况下,窗函数的长度会和信号的长度相同,而数据重叠的量通常会比窗函数的长度小。
在计算功率谱时,可以使用不同的窗函数来观察窗函数对功率谱的影响。通常来说,使用矩形窗可以得到最低的噪声水平,但同时也会导致功率谱的波动性较大。使用海明窗或 Blackman 窗可以减小功率谱的波动性,但同时也会增加噪声水平。因此,在使用窗函数时,需要根据实际情况来选择适当的窗函数。
参考
【1】matlab 功率谱分析