【计算机系统】校验码
- 校验码
- 奇偶校验码
- 海明码
- 校验位的位数
- 校验位的位置
- 确定校验的值
- 校验错误检测
- 循环冗余校验码
校验码
计算机系统运行时,为了确保数据在传送过程中正确无误,一是提高硬件电路的可靠性,二是提高代码的校验能力。通常使用校验码的方法来检测传送的数据是否出错。
校验码的基本思想是通过引入冗余信息并使用校验算法来检测和纠正数据的错误,从而提高数据的完整性和可靠性。具体如下。
奇偶校验码
e . g . e.g. e.g. 一个简单的例子
假设要传输的数据是 01010011,这是一个8位的二进制数。
奇校验: 在奇校验中,需要确保总共包含奇数个1。首先,计算数据中的1的数量,这里有4个1。为了保证总共有奇数个1,需要在数据末尾添加一个1,使其变成 010100111。这个额外的末尾的 1 就是奇校验位。
偶校验: 在偶校验中,需要确保总共包含偶数个1。计算数据中的1的数量,这里有4个1,为了保证总共有偶数个1,需要在数据末尾添加一个0,使其变成 010100110。这个额外的末尾的 0 就是偶校验位。
海明码
海明码在数据位之间的特定位置上插入 k k k 个校验位,通过校验位与数据位结合的异或方法来检错和纠错。
校验位的位数
设数据位是
n
n
n 位,校验位是
k
k
k 位,则
n
n
n 和
k
k
k 必须满足以下关系:
2
k
−
1
≥
n
+
k
2^k-1 ≥ n+k
2k−1≥n+k
假设对于 8 位的数据位,进行海明校验需要 4 个校验位: 2 3 − 1 < 8 + 3 , 2 4 − 1 ≥ 8 + 4 2^3-1 < 8+3,2^4-1 ≥ 8+4 23−1<8+3,24−1≥8+4
校验位的位置
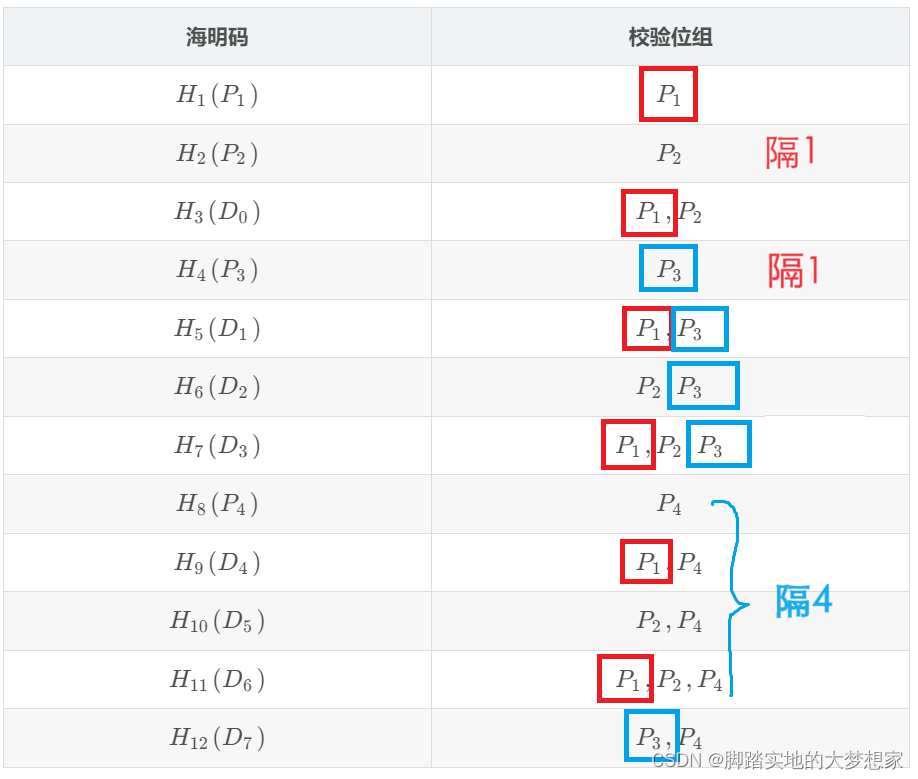
海明码校验位的位置,又称为海明码的编码规则。
设:
- k k k 个校验位为 P k , P k − 1 , . . . , P 1 P_k, P_{k-1}, ... , P_{1} Pk,Pk−1,...,P1;
- n n n 个数据位为 D n − 1 , D n − 2 , . . . , D 0 D_{n-1}, D_{n-2}, ... , D_{0} Dn−1,Dn−2,...,D0;
- 对应的海明码为 H n + k , H n + k − 1 , . . . , H 1 H_{n+k}, H_{n+k-1}, ... , H_{1} Hn+k,Hn+k−1,...,H1;
那么:
-
P
i
P_i
Pi 在海明码的第
2
i
−
1
2^{i-1}
2i−1 位置,即
H
j
=
P
i
H_j = P_i
Hj=Pi,
j
=
2
i
−
1
j=2^{i-1}
j=2i−1,数据位则依序从低到高占据海明码中剩余的位置:
- 8 位数据位 D 7 , D 6 , D 5 , D 4 , D 3 , D 2 , D 1 , D 0 D_7, D_6, D_5, D_4, D_3, D_2, D_1, D_0 D7,D6,D5,D4,D3,D2,D1,D0,4 位校验位 P 4 , P 3 , P 2 , P 1 P_4, P_3, P_2, P_1 P4,P3,P2,P1,形成的海明码 H 12 , H 11 , . . . , H 3 , H 2 , H 1 H_{12}, H_{11}, ... , H_3, H_2, H_1 H12,H11,...,H3,H2,H1;
- 确定数据位与校验位的位置:
- 校验码的位置在
2
0
,
2
1
,
2
2
,
2
3
2^0, 2^1, 2^2, 2^3
20,21,22,23 位置;

- 校验码的位置在
2
0
,
2
1
,
2
2
,
2
3
2^0, 2^1, 2^2, 2^3
20,21,22,23 位置;
确定校验的值
- 奇校验与偶校验:
- 奇校验中,校验位的值设置为确保相关数据位中包含奇数个1。如果数据位中包含偶数个1,校验位为1,以确保总和为奇数。
- 偶校验中,校验位的值设置为确保相关数据位中包含偶数个1。如果数据位中包含奇数个1,校验位为1,以确保总和为偶数。
- 校验位校验位置:
- 校验位 P 1 P_1 P1 校验位置 1 , 3 , 5 , 7 , 9 , . . . 1, 3, 5, 7, 9, ... 1,3,5,7,9,...(拿1隔1)
- 校验位 P 2 P_2 P2 校验位置 2 , 3 , 6 , 7 , 10 , 11 , . . . 2, 3, 6, 7, 10, 11, ... 2,3,6,7,10,11,...(拿2隔2)
- 校验位 P 3 P_3 P3 校验位置 4 , 5 , 6 , 7 , 12 4, 5, 6, 7, 12 4,5,6,7,12(拿4隔4)
- 校验位 P 4 P_4 P4 校验位置 8 , 9 , 10 , 11 , 12 8, 9, 10, 11, 12 8,9,10,11,12(拿5隔5)
- 校验的值(偶校验):
- P 1 = D 0 ⨁ D 1 ⨁ D 3 ⨁ D 4 ⨁ D 6 P_1 = D_0 \bigoplus D_1 \bigoplus D_3 \bigoplus D_4 \bigoplus D_6 P1=D0⨁D1⨁D3⨁D4⨁D6
- P 2 = D 0 ⨁ D 2 ⨁ D 3 ⨁ D 5 ⨁ D 6 P_2 = D_0 \bigoplus D_2 \bigoplus D_3 \bigoplus D_5 \bigoplus D_6 P2=D0⨁D2⨁D3⨁D5⨁D6
- P 3 = D 1 ⨁ D 2 ⨁ D 3 ⨁ D 7 P_3 = D_1 \bigoplus D_2 \bigoplus D_3 \bigoplus D_7 P3=D1⨁D2⨁D3⨁D7
- P 4 = D 4 ⨁ D 5 ⨁ D 6 ⨁ D 7 P_4 = D_4 \bigoplus D_5 \bigoplus D_6 \bigoplus D_7 P4=D4⨁D5⨁D6⨁D7
- 其中 ⨁ \bigoplus ⨁ 异或,不同为1,相同为0;
校验错误检测
校验的检测方案如下:
- G 1 = P 1 ⨁ D 0 ⨁ D 1 ⨁ D 3 ⨁ D 4 ⨁ D 6 G_1 = P_1 \bigoplus D_0 \bigoplus D_1 \bigoplus D_3 \bigoplus D_4 \bigoplus D_6 G1=P1⨁D0⨁D1⨁D3⨁D4⨁D6
- G 2 = P 2 ⨁ D 0 ⨁ D 2 ⨁ D 3 ⨁ D 5 ⨁ D 6 G_2 = P_2 \bigoplus D_0 \bigoplus D_2 \bigoplus D_3 \bigoplus D_5 \bigoplus D_6 G2=P2⨁D0⨁D2⨁D3⨁D5⨁D6
- G 3 = P 1 ⨁ D 1 ⨁ D 2 ⨁ D 3 ⨁ D 7 G_3 = P_1 \bigoplus D_1 \bigoplus D_2 \bigoplus D_3 \bigoplus D_7 G3=P1⨁D1⨁D2⨁D3⨁D7
- G 4 = P 1 ⨁ D 4 ⨁ D 5 ⨁ D 6 ⨁ D 7 G_4 = P_1 \bigoplus D_4 \bigoplus D_5 \bigoplus D_6 \bigoplus D_7 G4=P1⨁D4⨁D5⨁D6⨁D7
- 若采取偶校验,则当 G 4 G 3 G 2 G 1 G_4G_3G_2G_1 G4G3G2G1 全为 0 时,接收到的数据无错误。(奇校验全部为1);
e . g . e.g. e.g. 若采取偶校验, G 4 G 3 G 2 G 1 = 1010 G_4G_3G_2G_1=1010 G4G3G2G1=1010,说明 H 10 ( D 5 ) H_{10}(D_5) H10(D5)出错,将其取反即可纠正错误。
循环冗余校验码
循环冗余校验码(CRC, Cyclic Redundancy Check)是一种用于检查数据传输或存储时是否出现错误的算法。
其基本原理是对待发送的原始数据添加一些冗余的数据,使得整个数据的CRC值为0,接收方在接收到数据后重新计算CRC,如果值不为0,则说明数据在传输过程中有错误。
e . g . e.g. e.g. 一个简单的例子如下,其中CRC使用的多项式是CRC-4: x 4 + x + 1 x^4 + x + 1 x4+x+1
原始数据: 1101
添加0: 11010000
生成多项式: 10011(因为
x
4
+
x
+
1
x^4 + x + 1
x4+x+1 转换为二进制为 10011)
开始模2除法:
11010000
10011 <-- 第一次异或
---------
01001000 <-- 结果,移动到下一位,重复异或操作
10011
---------
00000100
10011
---------
00100010
10011
---------
00110001
从上面的结果,我们可以看到余数为 `0001`,所以CRC值为`0001`。
如此,我们得到的CRC值是 0001,因此,发送的数据应该是 11010001 。接收端收到这个数据后,可以用相同的方法再次计算CRC,如果计算出的CRC为 0000,则说明数据没有错误。
此上,为三个校验码,即 奇偶校验码、海明码与循环冗余校验码。