一、内容介绍
该测量系统基于三轴加速度和三轴陀螺仪,安装在钻柱内部,随钻柱一起旋转,形成捷联惯性导航系统,安装如下图所示:
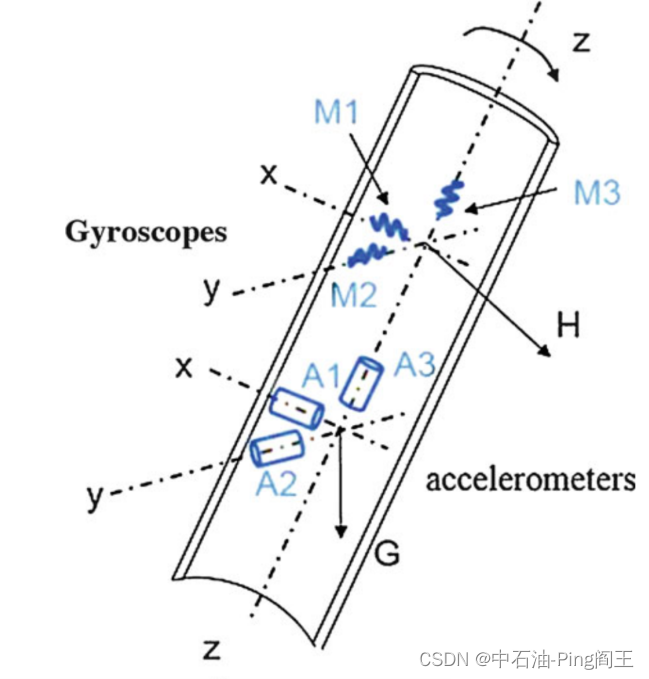
假设三轴加速度和陀螺仪的输出为:
f
b
=
[
f
x
f
y
f
z
]
T
f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z} \end{bmatrix}^T
fb=[fxfyfz]T
w
b
=
[
w
x
w
y
w
z
]
T
w^b=\begin{bmatrix}w_{x} & w_{y} &w_{z} \end{bmatrix}^T
wb=[wxwywz]T
使用这六轴的输出可以非常有效的求解姿态,应用惯性导航的求解算法,可以实现钻孔时的连续测量。加速度计和陀螺仪可以在坐标系中提供线加速度和角速度。但是,如果要求解钻具的位姿,则需要将该坐标系转换为另一个坐标系。
Xe、Ye、Ze三个轴代表地球坐标系。导航坐标系用于计算载体的位置、速度和姿态,因为导航坐标系沿当地的北、东、垂直方向,如下图中的“N, E, UP”,其中λ为经度角,φ为纬度角。在载体坐标系下,利用INS力学方程可得到井斜、井向和工具面角。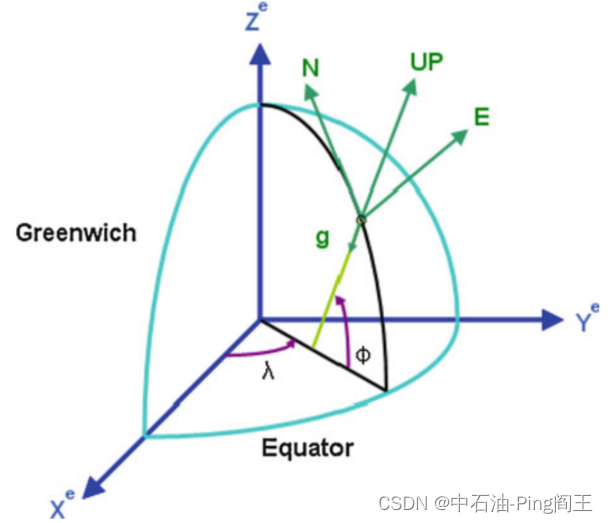
将b系统中测得的加速度和角速度值通过变换矩阵Rn b转换为n系统,即可求解井底工具的空间位置和姿态[28]。定义底部的经度为λ,纬度为φ,海拔为h,则其位置可表示为:
r
n
=
[
φ
λ
h
]
T
r^n=\begin{bmatrix}φ & λ &h \end{bmatrix}^T
rn=[φλh]T
定义n系统的速度分量,向北速度为Vn,向东速度为Ve,垂直速度为Vu。然后定义n系统的速度为:
r
n
=
[
V
e
V
n
V
u
]
T
r^n=\begin{bmatrix}V^e & V^n &V^u\end{bmatrix}^T
rn=[VeVnVu]T
速度分量可以表示为位置分量对时间的导数:
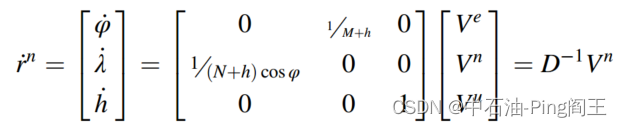
上式中,M为子午线的曲率半径,N为地球椭圆的曲率半径。
在载体坐标系下,加速度计
f
b
=
[
f
x
f
y
f
z
]
T
f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z}\end{bmatrix}^T
fb=[fxfyfz]T 通过变换矩阵
R
b
n
R^n_{b}
Rbn转换到地理坐标系的测量值为:

n坐标系中的加速度分量
f
n
f^n
fn可以对速度分量
v
n
v^n
vn积分。但由于地球本身的存在,会影响求解过程。地球自转速度为
w
e
=
15
d
e
g
/
h
r
w^e=15deg/hr
we=15deg/hr,用n坐标系表示的角速度矢量如下式所示:
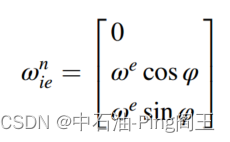
地理坐标系的变化取决于导航坐标系中北方和垂直方向的定义。北方方向通常指向子午线方向,垂直方向指向地球表面,如下图所示: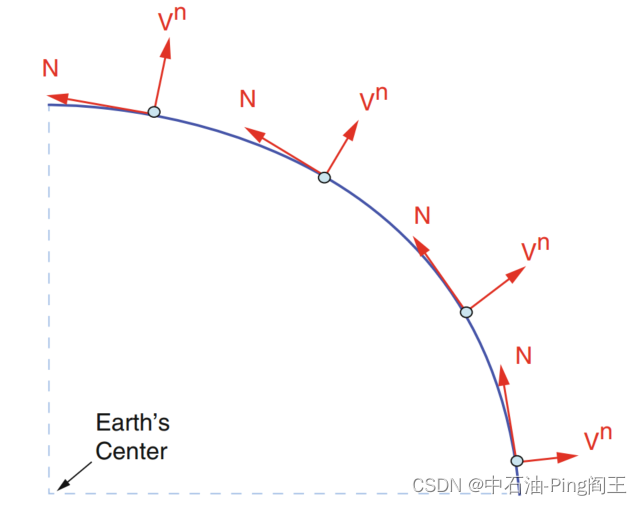
在导航坐标系中,角速度矢量可表示为:
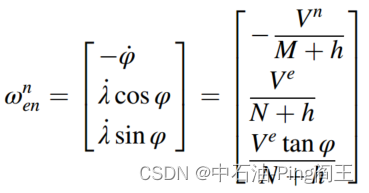
地球引力也影响IMU的加速度测量。我们可以用重力模型来修正。地球重力场可以表示为: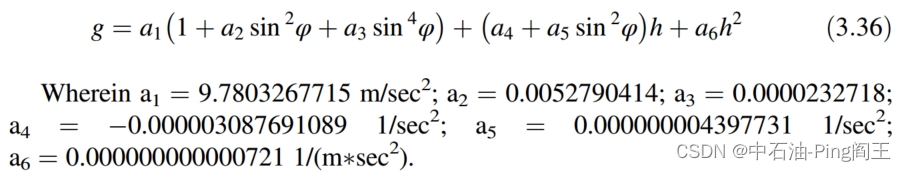
地球引力场在n系列中可以表示为:
g
n
=
[
0
0
−
g
]
g^n=\begin{bmatrix}0&0&-g\end{bmatrix}
gn=[00−g].考虑到地球因素的影响,速度分量Vn的变化率可以表示为: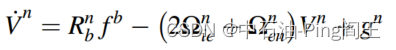
其中:
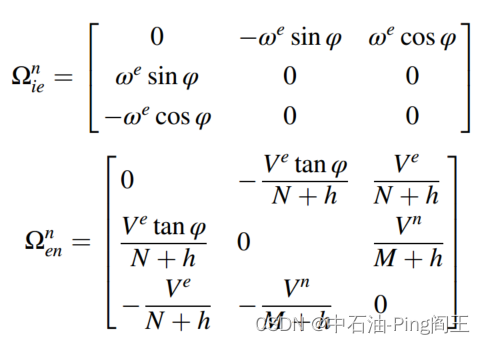
变换矩阵
R
b
n
R^n_{b}
Rbn可由以下微分方程得到:
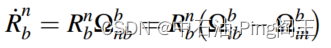
其中
Ω
i
b
b
Ω^b_{ib}
Ωibb为陀螺仪测得的角速度的反对称矩阵,角速度矢量
Ω
i
b
b
Ω^b_{ib}
Ωibb可表示为:
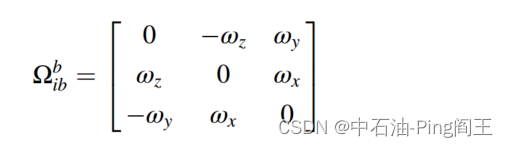
陀螺仪测量底部钻具的角速度,同时也测量地球自转的角速度和导航坐标系的方向。因此,需要从
Ω
i
b
b
Ω^b_{ib}
Ωibb中减去角速度
Ω
i
n
b
Ω^b_{in}
Ωinb,以消除这两个因素的影响。角速度矢量
Ω
i
n
b
Ω^b_{in}
Ωinb包含两部分,第一部分是地球自转速度
Ω
i
e
b
Ω^b_{ie}
Ωieb和导航坐标系方向变化速度
Ω
e
n
b
Ω^b_{en}
Ωenb,如下图所示: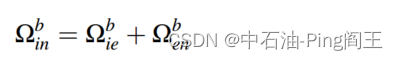
速度矩阵的反对称矩阵可以表示为: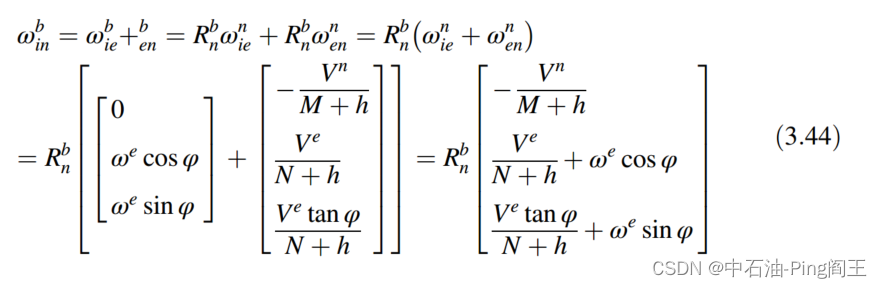
最后得到变换矩阵如下: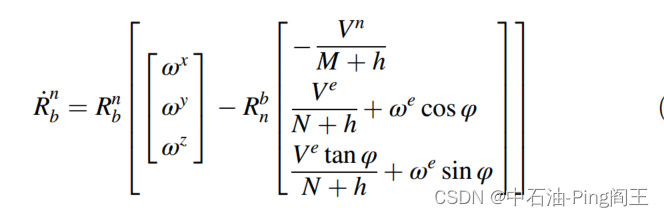
定义井斜角为θ,方位角为ψ,工具面为φ,变换矩阵
R
b
n
R^n_{b}
Rbn可表示为: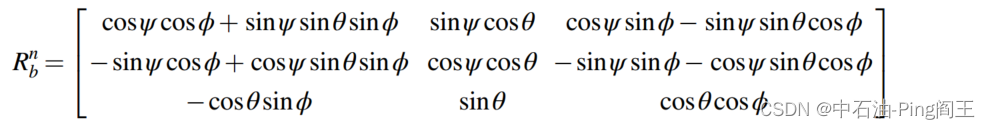
根据前面的假设,三轴加速度计的输出信号为:
f
b
=
[
f
x
f
y
f
z
]
T
f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z} \end{bmatrix}^T
fb=[fxfyfz]T 三轴陀螺仪的输出信号为:
w
b
=
[
w
x
w
y
w
z
]
T
w^b=\begin{bmatrix}w_{x} & w_{y} &w_{z} \end{bmatrix}^T
wb=[wxwywz]T 从测量的角速度可以计算出角度变化量:

同样,由加速度的测量值可以计算出线速度: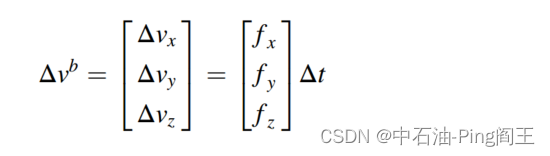
考虑到地球自转和导航坐标系方向变化的影响,在时刻tk时,角度的增加可表示为: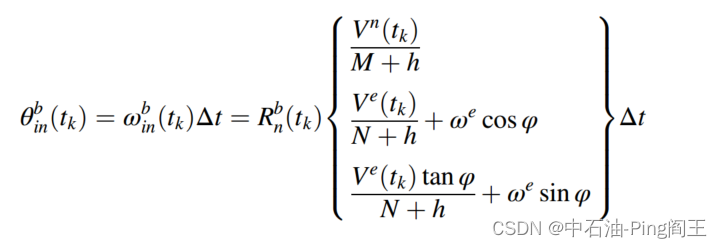
然后,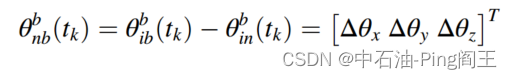
综上所述,基于地理坐标系的捷联惯性导航系统的力学方程如下:
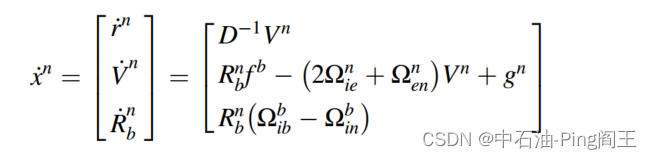
上式的解可以用欧拉角法、方向余弦法或四元数法求解。通过在载体轴上安装三轴加速度计和三轴陀螺仪,可以通过测量值获得载体的姿态、速度和位置等信息。
二、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)


![socket.error: [Errno 10049]错误](https://img-blog.csdnimg.cn/eba3ada035f14233b92c5b963b452be3.png)