题目描述

思路讲解

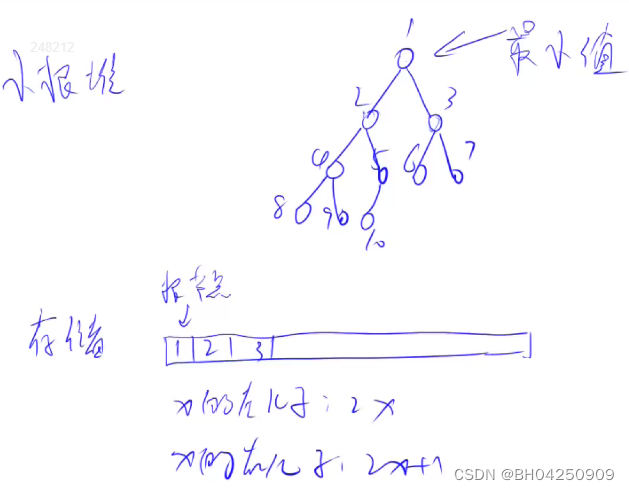
堆是一颗完全二叉树，除了最下面一层，其余是满的，最后一层从左到右排列
小根堆：每个点小于等于左右两堆，所以根节点就是最小值
大根堆：每个点大于等于左右两堆，所以根节点就是最大值

堆的介绍：

代码展示

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], cnt;

void down(int u) {
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t) {
        swap(h[u], h[t]);
        down(t);
    }
}


int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
    cnt = n;

    // 构建堆
    for (int i = n / 2; i; i--) down(i);

    while (m--) {
        printf("%d ", h[1]);

        // 重构堆
        h[1] = h[cnt--];
        down(1);
    }

    puts("");

    return 0;
}

解释代码：

// 构建堆
for (int i = n / 2; i; i–) down(i);
这段代码是在构建最小堆的过程中使用的循环。最小堆是一种数据结构，其中每个节点的值都小于或等于其子节点的值。这段代码的目的是将一个数组 h 转化为最小堆。

让我解释循环的工作原理：

1. i 的初始值是 n / 2，其中 n 是数组 h 的大小。这是因为数组 h 的后半部分元素都是叶子节点，不需要进行下沉操作，所以我们从数组的中间位置向前遍历，对每一个非叶子节点进行下沉操作。

2. 在每一次迭代中，down(i) 函数被调用，它的作用是将以索引 i 为根的子树调整为最小堆。这是通过比较根节点 h[i] 与其左子节点 h[i * 2] 和右子节点 h[i * 2 + 1] 的值来完成的。

3. 如果左子节点的值比根节点小，或者右子节点的值比根节点小，那么就会交换根节点和相应子节点的值，以确保根节点的值小于等于其子节点的值。

4. 然后，递归调用 down(t)，其中 t 是交换后的子节点的索引，以继续下沉操作，确保子树仍然是一个最小堆。

5. 这个循环会持续进行，直到 i 变为0为止，从数组的底部向上逐渐构建最小堆，最终使整个数组 h 成为一个满足最小堆性质的结构，其中最小的元素位于堆的根部（即h[1]）。

总之，这段代码的作用是在构建最小堆的过程中，通过从数组的中间位置向前遍历，对每一个非叶子节点应用 down 操作，以确保整个数组 h 成为一个最小堆。这个最小堆可以用于高效地选择和移除最小的元素，实现堆排序和其他算法。