文章目录
- 正文
- Methodology 方法论
- Origins and applications 起源和应用
- How it works 它是怎样工作的
- The stochastic optimization problem 随机优化问题
- Virtual queues 虚拟队列
- The drift-plus-penalty expression 漂移加惩罚表达式
- Drift-plus-penalty algorithm
- Approximate scheduling 近似调度
- 参考资料
正文
在概率论的数学理论中,漂移加惩罚法被用于优化排队网络和其他随机系统。
该技术用于稳定排队网络,同时最小化网络惩罚函数的平均时间。它可用于优化性能目标,如时间平均功率、吞吐量和吞吐量效用。在不需要最小化惩罚的特殊情况下,当目标是在多跳网络中设计稳定的路由策略时,该方法可以简化为背压路由。漂移加惩罚法也可用于最小化受时间平均约束的随机过程对其他随机过程集合的时间平均。这是通过定义一组适当的虚拟队列来实现的。它还可以用于生成凸优化问题的时间平均解。
Methodology 方法论
漂移加惩罚方法适用于离散时间时隙
t
t
t 在
0
,
1
,
2
,
…
{0,1,2,…}
0,1,2,… 中运行的排队系统。首先,非负函数
L
(
t
)
L(t)
L(t) 被定义为时间t时所有队列状态的标量度量。函数
L
(
t
)
L(t)
L(t) 通常被定义为时间
t
t
t 时所有队列大小的平方和,称为李雅普诺夫函数。李亚普诺夫漂移定义如下:
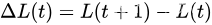
每个时隙
t
t
t,观察当前队列状态,并采取控制动作贪婪地最小化以下漂移+惩罚表达式的边界:

其中 p ( t ) p(t) p(t) 是罚函数 V V V 是一个非负的权值。可以选择 V V V 参数,以确保 p ( t ) p(t) p(t) 的时间平均值任意接近最优值,并在平均队列大小上进行相应的权衡。与背压路由一样,这种方法通常不需要了解工作到达和网络移动性的概率分布。
Origins and applications 起源和应用
当 V = 0 V=0 V=0,该方法简化为贪婪地最小化李雅普诺夫漂移。这就是最初由Tassiulas和Ephremides开发的背压路由算法(也称为最大权重算法)。
Neely和Neely, Modiano, Li在漂移表达式中加入了 V p ( t ) Vp(t) Vp(t) 项,以在稳定网络的同时最大化吞吐量效用函数。为此,惩罚 p ( t ) p(t) p(t) 被定义为 − 1 -1 −1 倍。 这种漂移加惩罚技术后来被用于最小化平均功率并优化其他惩罚和奖励指标。
该理论主要用于优化通信网络,包括无线网络、自组织移动网络和其他计算机网络。然而,数学技术可以应用于其他随机系统的优化和控制,包括智能电网中的可再生能源分配和产品装配系统的库存控制。
How it works 它是怎样工作的
本节展示如何使用漂移加惩罚方法来最小化受其他函数集合的时间平均约束的函数 p ( t ) p(t) p(t) 的时间平均。(就是说要最小化 p ( t ) p(t) p(t) 的时间平均,但是同时受到其它时间平均的约束)。
The stochastic optimization problem 随机优化问题
考虑一个离散时间系统,它在规范化时隙 t = 0 , 1 , 2 , … t={0,1,2,…} t=0,1,2,… 上变化。定义 p ( t ) p(t) p(t) 为需要将时间平均值最小的函数,称为惩罚函数。假设 p ( t ) p(t) p(t) 的时间平均值的最小化必须在 K K K 个其他函数集合的时间平均值约束下完成:
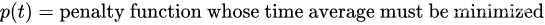
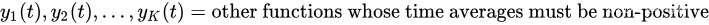
每个时隙
t
t
t,网络控制器观察到一个新的随机事件。然后,它根据对该事件的了解做出控制动作。将
p
(
t
)
p(t)
p(t) 和
y
i
(
t
)
y_i(t)
yi(t) 的值确定为随机事件和时隙
t
t
t 的控制作用的函数:
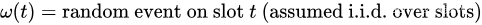
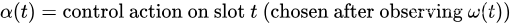
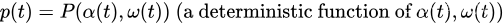
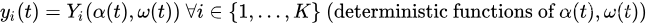
小写符号 p ( t ) p(t) p(t), y i ( t ) y_i(t) yi(t) 和大写符号 P ( ) P() P(), Y i ( ) Y_i() Yi() 用于区分惩罚值和根据随机事件和时隙 t t t 的控制作用确定这些值的函数。
假设随机事件
ω
(
t
)
\omega (t)
ω(t) 在一些抽象的事件集合
Ω
Ω
Ω 中取值。
假设控制动作
α
(
t
)
\alpha (t)
α(t) 是在某个包括控制项抽象集合
A
A
A 中选择的。
集合
Ω
\Omega
Ω 和
A
A
A 是任意的,可以是有限的也可以是无限的。
例如,
A
A
A 可以是抽象元素的有限列表,实值向量的不可数无限(可能是非凸的)集合,等等。函数
P
(
)
P()
P(),
Y
_
i
(
)
Y_i()
Y_i() 也是任意的,不需要连续性或凸性假设。
以通信网络中的随机事件为例
ω
(
t
)
\omega (t)
ω(t) 可以是一个向量,它包含每个节点时隙
t
t
t 时的到达信息和每个链路的时隙
t
t
t 时的信道状态信息。
控制动作
α
(
t
)
\alpha (t)
α(t) 可以是包含每个节点的路由和传输决策的向量。
函数
P
(
)
P()
P() 和
Y
_
i
(
)
Y_i()
Y_i() 可以表示与时隙
t
t
t 的控制动作和通道条件相关的功率消耗或吞吐量。
为了说明简单,假设
P
(
)
P()
P() 和
Y
i
(
)
Y_i()
Yi() 函数是有界的。进一步假设随机事件过程
ω
(
t
)
\omega(t)
ω(t) 在槽
t
t
t 上独立且同分布,具有一些可能未知的概率分布。目标是设计一个策略,使控制行动随着时间的推移,以解决以下问题:

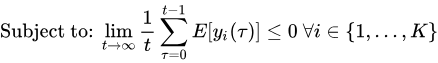
即最小化惩罚项的时间平均值,同时维持队列的稳定。
自始至终都假定这个问题是可行的。也就是说,假设存在一种算法可以满足所有 K K K 个期望约束。
上述问题以抽象过程 y i ( t ) y_i(t) yi(t) 非正的时间平均期望的标准形式提出了每个约束。这种方法不会失去通用性。例如,假设某人希望某个过程 a ( t ) a(t) a(t)的时间平均期望小于或等于给定常数 c c c。那么可以定义一个新的惩罚函数 y ( t ) = a ( t ) − c y(t) = a(t) - c y(t)=a(t)−c,并且期望的约束等价于 y ( t ) y(t) y(t)的时间平均期望是非正的。同样,假设有两个过程 a ( t ) a(t) a(t)和 b ( t ) b(t) b(t),并且希望 a ( t ) a(t) a(t)的时间平均期望小于或等于 b ( t ) b(t) b(t)的时间平均期望。这个约束通过定义一个新的惩罚函数 y ( t ) = a ( t ) − b ( t ) y(t) = a(t) - b(t) y(t)=a(t)−b(t)写成标准形式。上述问题寻求最小化抽象惩罚函数 p ′ ( t ) ′ p'(t)' p′(t)′的时间平均值。这可以通过定义 p ( t ) = − r ( t ) p(t) = - r(t) p(t)=−r(t)来最大化某些理想奖励函数 r ( t ) r(t) r(t)的时间平均值。
Virtual queues 虚拟队列
对于
{
1
,
…
,
K
}
\{1,…, K\}
{1,…,K}中的每个约束
i
i
i,定义一个在时隙
t
=
{
0
,
1
,
2
,
.
.
.
}
t=\{0,1,2,...\}
t={0,1,2,...} 上动态的虚拟队列,如下:
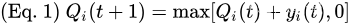
对所有
i
∈
{
1
,
.
.
.
,
K
}
i∈\{1,...,K\}
i∈{1,...,K} 初始化
Q
i
(
0
)
=
0
Q_i(0) = 0
Qi(0)=0 。该更新方程与虚拟离散时间队列积压
Q
i
(
t
)
Q_i(t)
Qi(t)相同,其中
y
i
(
t
)
y_i(t)
yi(t) 为时隙
t
t
t 上新到达和新服务机会之间的差。直观地说,稳定这些虚拟队列确保约束函数的时间平均值小于或等于零,因此满足期望的约束。要准确地理解这一点,请注意(式1)意味着:
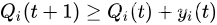
因此
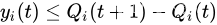
利用伸缩和定律对前
t
t
t 个槽求和,可得:
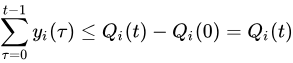
除以t,取期望:
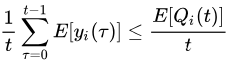
因此,当对于所有
i
∈
{
1
,
…
K
}
i∈\{1,…K\}
i∈{1,…K} 中所有i满足下列条件时,问题的期望约束得到满足:

满足上述极限方程的队列 Q i ( t ) Q_i(t) Qi(t) 被称为是平均速率稳定的。
The drift-plus-penalty expression 漂移加惩罚表达式
为了稳定队列,定义Lyapunov函数 L ( t ) L(t) L(t)作为槽位 t t t上队列积压总量的度量:
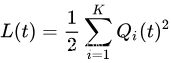
将排队方程(Eq. 1)平方,得到每个
i
∈
{
1
,
.
.
.
,
K
}
i∈\{1,...,K\}
i∈{1,...,K}的队列的下列边界:
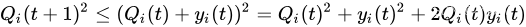
因此,
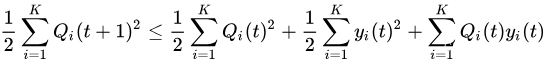
由此得出
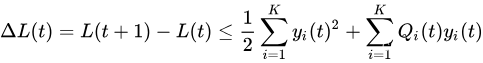
现在把
B
B
B 定义为一个正常数,它是上面不等式右边第一项的上界。因为
y
i
(
t
)
y_i(t)
yi(t) 的值是有界的,所以存在这样一个常数。则:

两边同时加上
V
p
(
t
)
Vp(t)
Vp(t),得到漂移加惩罚表达式的边界如下:
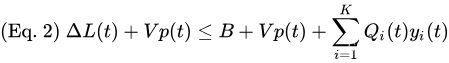
漂移+惩罚算法(定义如下)使控制动作在每个槽
t
t
t上贪婪地最小化上述不等式的右侧。
直观地说,仅采取最小化漂移的操作在队列稳定性方面是有益的,但不会最小化惩罚项的时间平均值。仅仅采取最小化惩罚的措施并不一定会稳定队列。
因此,采取最小化加权总和的动作同时包含了队列稳定性和惩罚最小化的目标。可以调整权重V,以或多或少地强调惩罚最小化,这将导致性能的权衡。
Drift-plus-penalty algorithm
让
A
A
A 是所有可能的控制动作的抽象集合。
在每个时隙
t
t
t,观察随机事件和当前队列值:
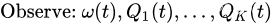
给定槽
t
t
t 的这些观察结果,贪婪地选择一个控制动作
α
(
t
)
∈
A
\alpha (t)\in A
α(t)∈A以最小化以下表达式:
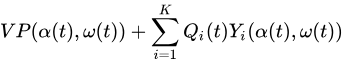
然后根据(式1)为
i
∈
{
1
,
…
,
K
}
i \in \{1,…, K\}
i∈{1,…,K} 更新队列,对时隙
t
+
1
t+1
t+1 重复此过程。
注意,当时隙 t t t 最小化的控制动作时,在槽 t t t 上观察到的随机事件和队列积压充当给定的常量。因此,每个槽都涉及对集合 A A A 的最小化控制动作的确定性搜索。该算法的一个关键特征是它不需要了解随机事件过程的概率分布。
Approximate scheduling 近似调度
上述算法涉及在抽象集合
A
A
A 上寻找一个函数的最小值。在一般情况下,最小值可能不存在,或者可能很难找到。
因此,假设算法以如下近似方式实现是有用的:定义
C
C
C为非负常数,并假设对于所有槽
t
t
t,在集合A中选择的控制动作
α
(
t
)
\alpha (t)
α(t)满足:
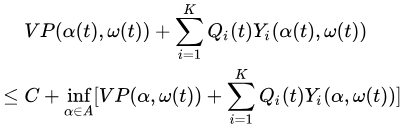
这样的控制作用称为 C-加性近似 。
C
=
0
C = 0
C=0 的情况对应于每个槽
t
t
t 上所需表达式的精确最小化。
参考资料
https://en.wikipedia.org/wiki/Drift_plus_penalty