决策树
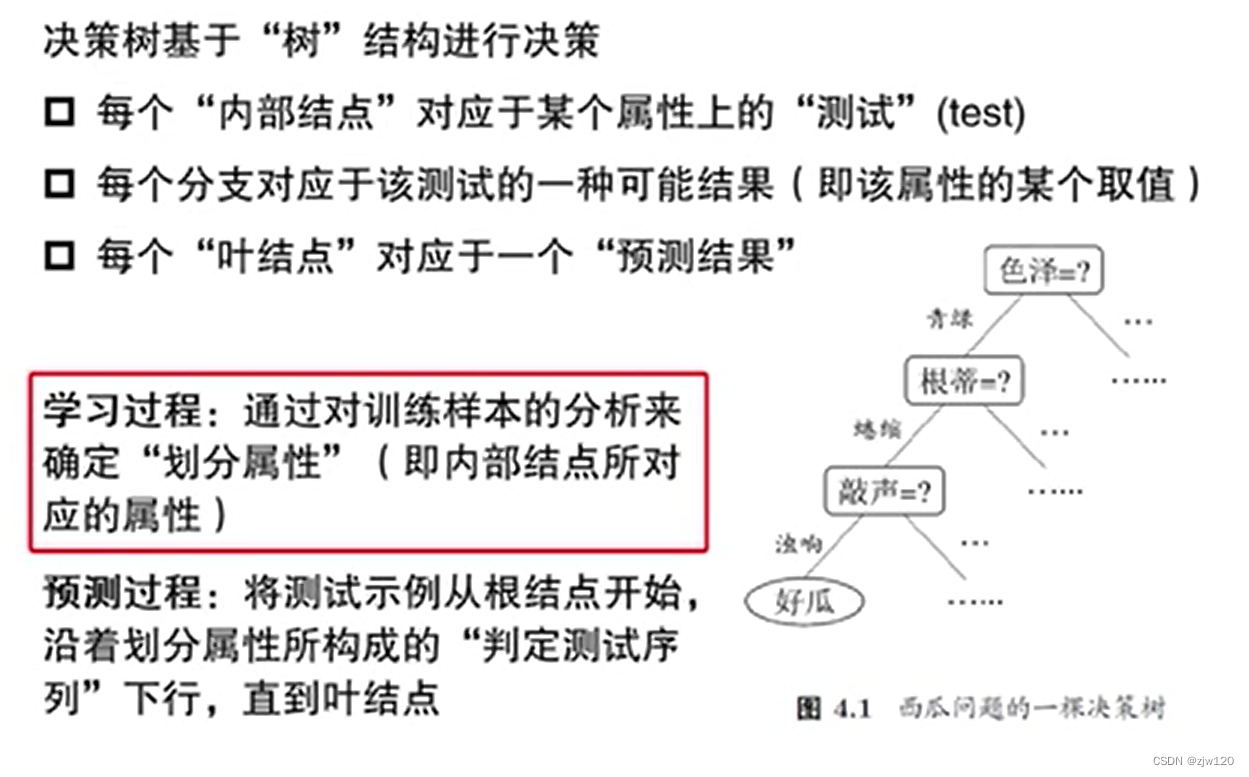

决策树划分时,当前属性集为空,或所有样本在所有属性上取值相同,将结点标记为叶节点,其类别标记为当前样本集中样本数最多的类。
决策树算法的核心在于:选择最优划分属性
判别分类的三种情形:
- 当前节点包含的样本全属于一个类别,则可视为叶子节点,分类就是本身
- 当前节点为空,则分类就是父类的分类
- 当前节点包含样本不全属于一个类别,那么多数作为类别

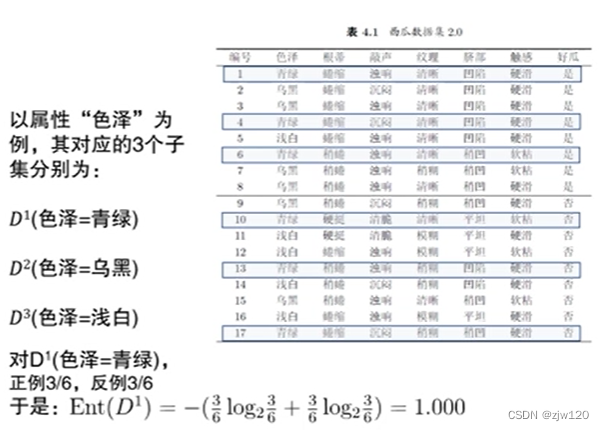
信息增益information gain

ID3
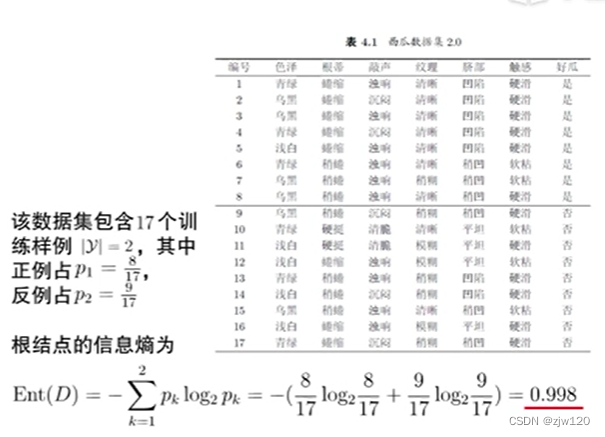
在二分类任务中,若当前样本集合的正类和负类的数量刚好各一半,此时信息熵为
E
n
t
(
D
)
=
−
(
1
2
l
o
g
2
1
2
+
1
2
l
o
g
2
1
2
)
=
1
Ent(D)=-(\frac{1}{2}log_{2}\frac{1}{2}+\frac{1}{2}log_{2}\frac{1}{2})=1
Ent(D)=−(21log221+21log221)=1
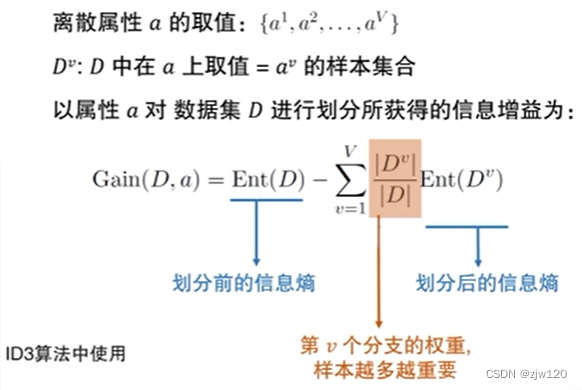
信息增益=划分前的信息熵-第v个分支的权重*划分后的信息熵
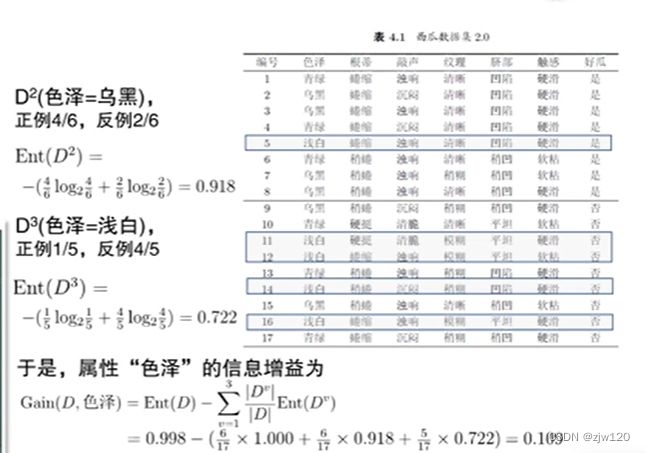
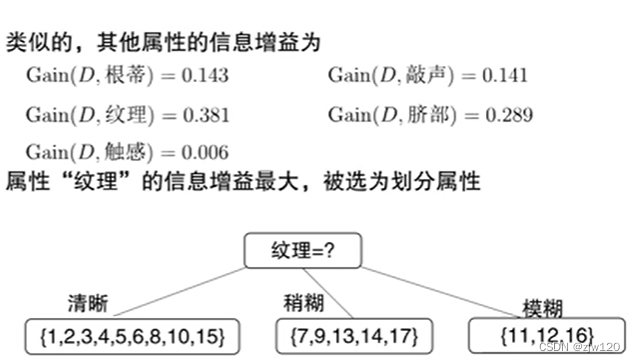

C4.5
I
V
(
a
)
IV(a)
IV(a)的形式是在做规范化,其把原来不可以直接比较的东西变得可比较。归一化是规范化的特例,归一化是把规范化的范围限制在[0,1]区间。
由于无法判断
G
a
i
n
(
D
,
a
)
Gain(D,a)
Gain(D,a)与
I
V
(
a
)
IV(a)
IV(a)之间应该是控制
G
a
i
n
(
D
,
a
)
Gain(D,a)
Gain(D,a)更大,还是控制
I
V
(
a
)
IV(a)
IV(a)更小,采用启发式的方法——先从候选划分属性中找出信息增益高于平均水平的,再从中选取增益率最高的。

CART算法,基尼指数
按照概率来理解,如果每次抓两个球,如果两次抓到的球属于同一类,说明候选属性集合比较纯;因此
G
i
n
i
(
D
)
Gini(D)
Gini(D)中,抓球抓到第一类的概率是
∑
k
=
1
∣
y
∣
p
k
\sum_{k=1}^{|y|}p_k
∑k=1∣y∣pk,抓球抓到第二类的概率是
∑
k
′
≠
k
p
k
′
\sum_{k \prime \ne k}p_k^{\prime}
∑k′=kpk′,如果二者乘积越小,数据集D的纯度越高。同理,用1-两次抓出相同类型球的概率(纯度)=不纯度,即
G
i
n
i
(
D
)
Gini(D)
Gini(D).

以上三种划分算法的区别
划分选择VS剪枝
划分选择的三种算法差异不明显;而剪枝方法和程度对决策树泛化性能的影响更为显著。

剪枝的目的在于尽量避免过拟合,基本策略包括预剪枝和后剪枝,评估剪枝前后的优劣用到第二章的评估方法。


缺失值的处理思路

样本赋权,权重划分


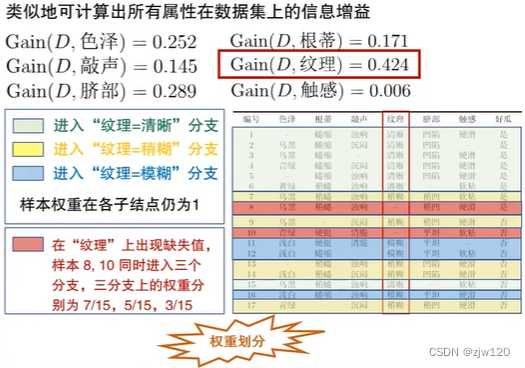
权重划分:给定划分属性,若样本在该属性上的值缺失,会按权重同时进入所有分支。
对于缺失值样本(红色),其在三个类别上的权重不再是1,而分别是7/15,5/15.3/15,注意,虽然有17个样本,但2个缺失,故分母取得15.
![[前端攻坚]:详解call、apply、bind的实现](https://img-blog.csdnimg.cn/c1228dcc49b842e98df6827dec716e20.png#pic_center)












![[Cortex-M3]-5-cache uncache](https://img-blog.csdnimg.cn/d8f74ce4d8ca4131990dd2dc4c34d21b.png)


