---

前言

1、左叶子之和
2、找树左下角的值
3、从中序与后序遍历序列构造二叉树
4、从中序与前序遍历序列构造二叉树
5、最大二叉树

---

一、左叶子之和（力扣404）

给定二叉树的根节点 root ，返回所有左叶子之和。

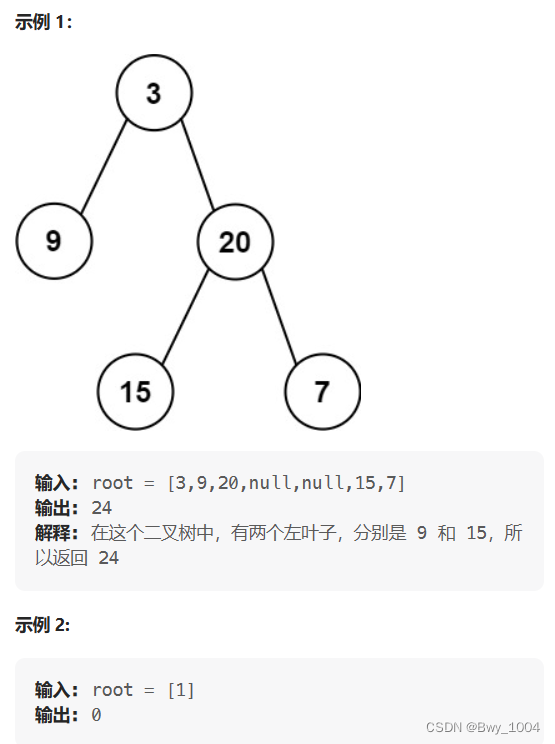
思路：
判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。

if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
    左叶子节点处理逻辑
}

1、递归遍历

class Solution {
    int res=0;
    public int sumOfLeftLeaves(TreeNode root) {
        //递归遍历
        if(root==null) return 0;
        postOrder(root);
        return res;
    }
    public void postOrder(TreeNode node){
        if(node==null) return ;
        postOrder(node.left);
        postOrder(node.right);
        if(node.left!=null && node.left.left==null && node.left.right==null){
            res += node.left.val;
        }
    }
}

2、非递归遍历

class Solution {

    public int sumOfLeftLeaves(TreeNode root) {
        //非递归遍历
        int res=0;
        if(root==null) return res;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            if(node.left!=null && node.left.left==null && node.left.right==null){
                res += node.left.val;
            }
            if(node.right!=null){
                stack.push(node.right);
            }
            if(node.left!=null){
                stack.push(node.left);
            }
        }
        return res;
    }
}

二、找树左下角的值（力扣513）

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

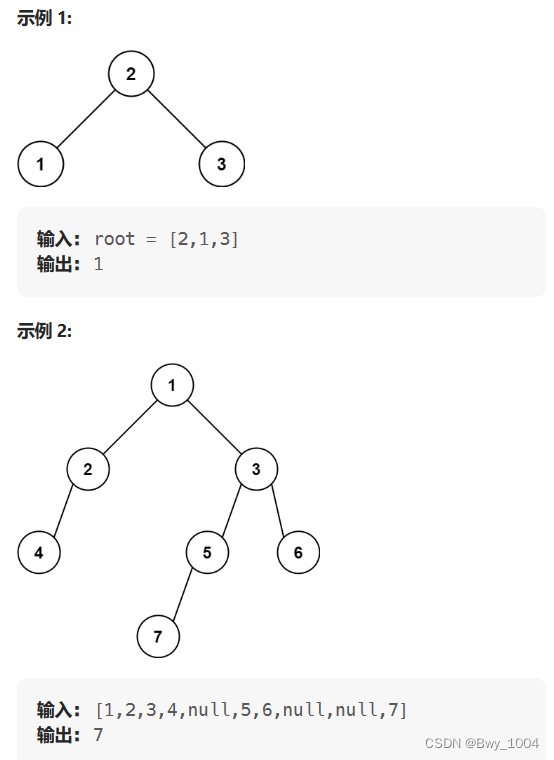
最底层：深度最大
最左边

1、迭代法（层序遍历）

最后一层的第一个值就是所要求的结果值

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        Queue<TreeNode> que = new LinkedList<>();
        if(root==null) return 0;
        que.offer(root);
        while(!que.isEmpty()){
            int len = que.size();
            List<Integer> itemList = new ArrayList<>();
            while(len-->0){
                TreeNode node = que.poll();
                itemList.add(node.val);
                if(node.left!=null){
                    que.offer(node.left);
                }
                if(node.right!=null){
                    que.offer(node.right);
                }
            }
            res.add(itemList);
        }
        return res.get(res.size()-1).get(0);
    }
}

2、递归法

class Solution {
    private int Deep = -1; //深度
    private int value = 0; //结果值
    public int findBottomLeftValue(TreeNode root) {
       //递归法
       value = root.val;
       findLeftValue(root,0);7
       return value;
    }
    public void findLeftValue(TreeNode root,int deep){
        if(root==null) return ;
        if(root.left==null && root.right==null){
            //叶子节点
            if(deep>Deep){
                value = root.val;
                Deep = deep;
            }
        }
        if(root.left!=null){
            deep++;
            findLeftValue(root.left,deep);
            deep--; //回溯
        }
        if(root.right!=null){
            deep++;
            findLeftValue(root.right,deep);
            deep--; //回溯
        }
    }
}

三、从中序与后序遍历序列构造二叉树（力扣106）

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

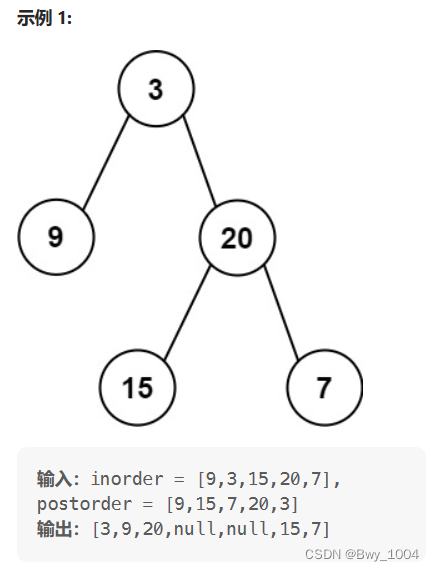
图解：

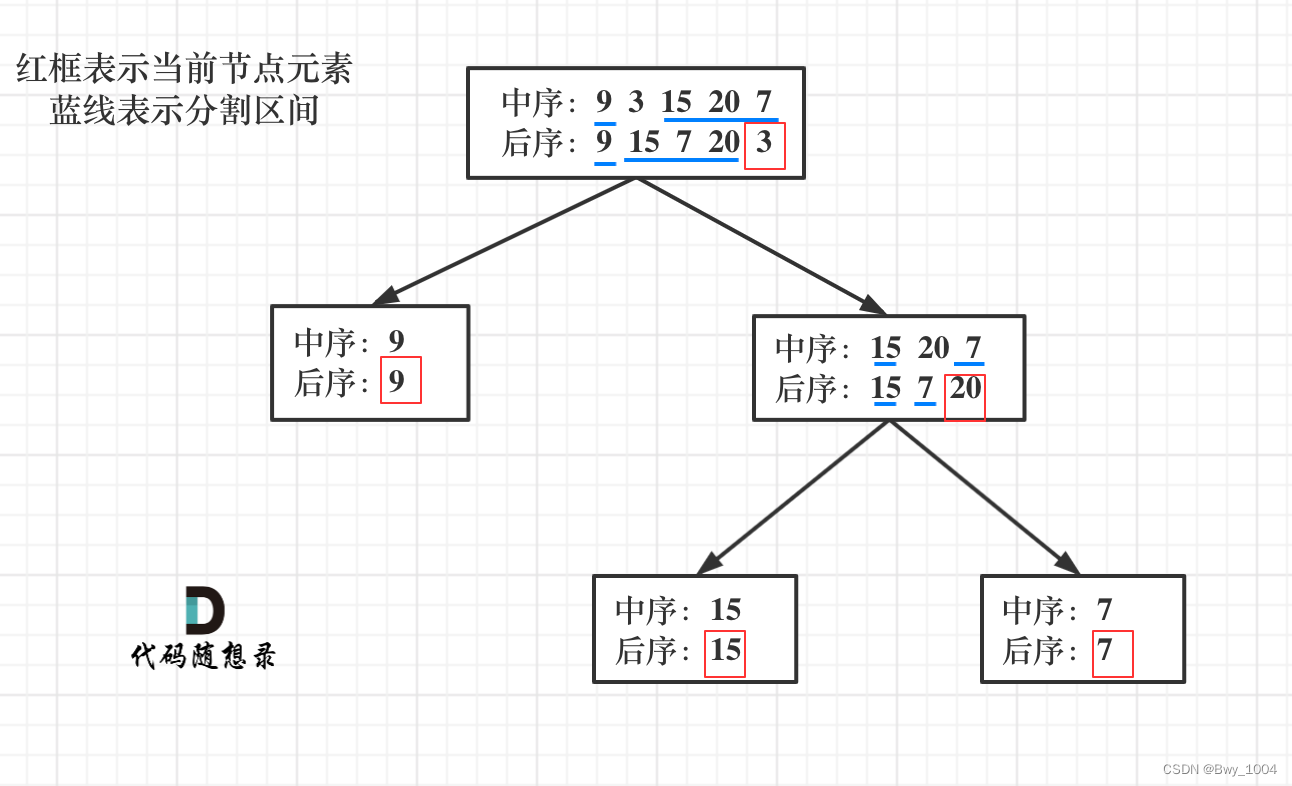
第一步：如果数组大小为零的话，说明是空节点了。

第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）

第五步：切割后序数组，切成后序左数组和后序右数组

第六步：递归处理左区间和右区间

class Solution {
    Map<Integer,Integer> map;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map = new HashMap<>();
        for(int i=0;i<inorder.length;i++){
            map.put(inorder[i],i);
        }
        return findNode(inorder,0,inorder.length,postorder,0,postorder.length);
    }
        //切割中序数组  左中序[0,index] [index+1,length-1]
        //切割后序数组  用切割中序数组拿到的左中序数组 来切左后中序
    public TreeNode findNode(int[] inorder,int inBegin,int inEnd,int[] postorder,int postBegin,int postEnd){
        if(inBegin >= inEnd || postBegin >= postEnd){
            return null;
        }
        int rootIndex = map.get(postorder[postEnd-1]);
        TreeNode root = new TreeNode(inorder[rootIndex]);//根节点
        int lenOfLeft = rootIndex - inBegin;
        root.left = findNode(inorder,inBegin,rootIndex, postorder,postBegin,postBegin+lenOfLeft);
        root.right = findNode(inorder, rootIndex+1,inEnd,postorder,postBegin+lenOfLeft,postEnd-1);
        return root;
    }
}

四、从中序与前序遍历序列构造二叉树（力扣105）

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

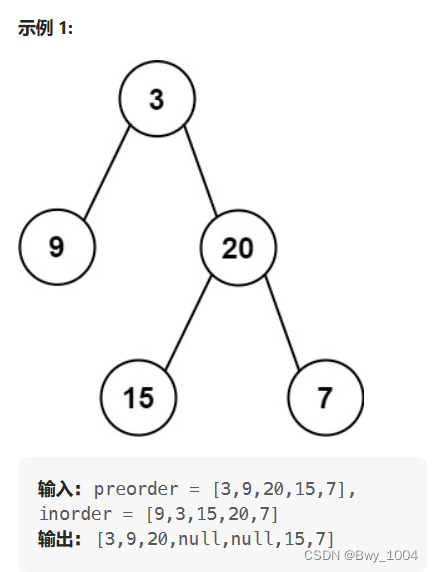
思路：
和第三题基本一致，注意参数的细微差别

class Solution {
    Map<Integer,Integer> map;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        map = new HashMap<>();
        for(int i=0;i<inorder.length;i++){
            map.put(inorder[i],i);
        }
        return findNode(preorder,0,preorder.length,inorder,0,inorder.length);
    }
    public TreeNode findNode(int[] preorder,int preBegin,int preEnd,int[] inorder,int inBegin,int inEnd){
        if(preBegin >= preEnd || inBegin >= inEnd) return null;
        int rootIndex = map.get(preorder[preBegin]);
        TreeNode root = new TreeNode(inorder[rootIndex]);
        int lenOfLeft = rootIndex - inBegin;
        root.left = findNode(preorder,preBegin+1,preBegin+lenOfLeft+1,inorder,inBegin,rootIndex);
        root.right = findNode(preorder,preBegin+lenOfLeft+1,preEnd,inorder,rootIndex+1,inEnd);
        return root;
    }
}

五、最大二叉树（力扣654）

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。

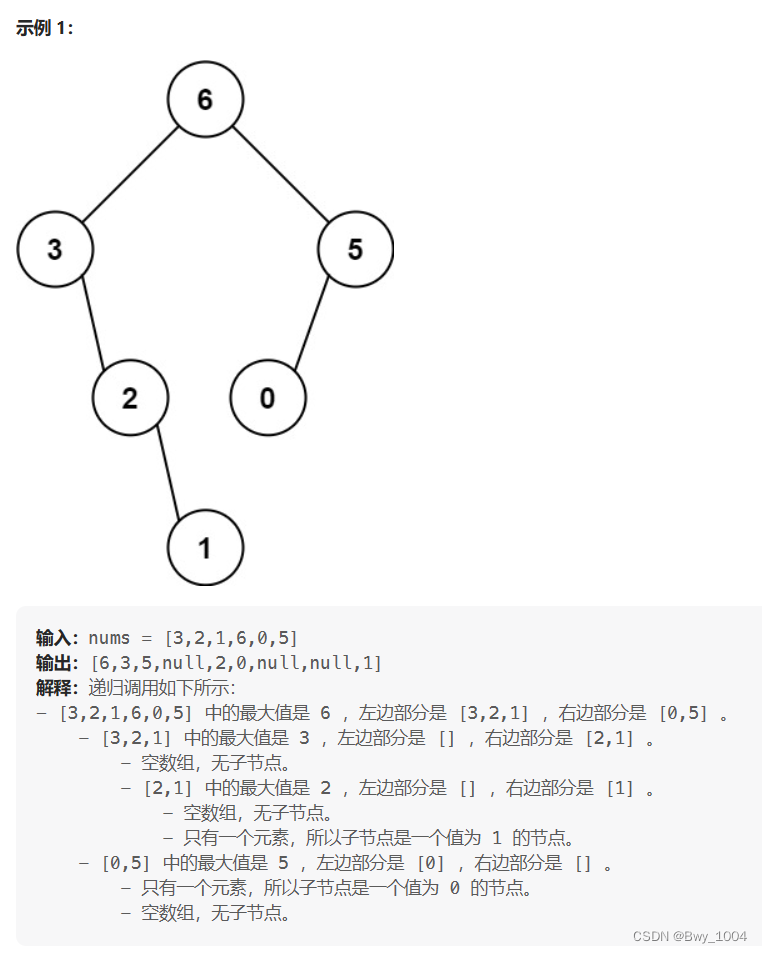
思路：
和第三题基本一致，注意参数的细微差别

class Solution {

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return buildTree(nums,0,nums.length);
    }
    public TreeNode buildTree(int[] nums,int leftIndex,int rightIndex){
        if (rightIndex - leftIndex < 1) {// 没有元素了
            return null;
        }
        if (rightIndex - leftIndex == 1) {// 只有一个元素
            return new TreeNode(nums[leftIndex]);
        }
        int rootIndex = leftIndex;
        int rootValue = nums[rootIndex];

        for(int i =leftIndex;i<rightIndex;i++ ){
            if(nums[i]>rootValue){
                rootValue = nums[i];
                rootIndex = i;
            } 
        }
        TreeNode root = new TreeNode(rootValue);
        root.left=buildTree(nums,leftIndex,rootIndex);
        root.right=buildTree(nums,rootIndex+1,rightIndex);
        return root;
    }
}

---