系列文章目录
第一章:PCL生成线段点云
第二章:PCL创建圆柱面点云
文章目录
- 系列文章目录
- 前言
- 一、三角形面是什么?
- 二、三角形面点云创建步骤
- 1.引入库
- 2.创建三角形面点云
- 总结
前言
点云库 (PCL) 是一个独立的、大规模的、开放的 2D/3D 图像和点云处理项目。PCL功能强大,但是却并不包含创建点云功能,尤其是一些常见的点云,如:线段、球、立方体、圆柱面等,而是仅在可视化visualization类中包含一些常见的几何形状,如:线段、球、立方体等,无法作为点云数据传递,因此打算自己写一下,本文是关于三角形面点云的创建。

一、三角形面是什么?
这是俺自己随便取的名字,主要是为了和三角形点云区分开来,简单来说就是给定空间内随便三个不共线的三维点,在这三个点组成的三角形内随机生成若干个点,填充成一个点云。
二、三角形面点云创建步骤
1.引入库
PCL环境配置参见:Windows系统下5分钟配置好PCL(debug和release)
代码如下:
#include <iostream>
#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
#include <pcl/visualization/pcl_visualizer.h>
2.创建三角形面点云
- 检查输入的三个点是否共线
- 生成三角形面点云
- 可视化验证
关键函数代码如下
//判断三个空间点是否共线
//param[in] p1, p2, p3: 输入的三个空间点
//param[out] bool:是否共线
bool arePointsCollinear(const pcl::PointXYZ& p1, const pcl::PointXYZ& p2, const pcl::PointXYZ& p3) {
// 计算两个向量
pcl::PointXYZ v1(p2.x - p1.x, p2.y - p1.y, p2.z - p1.z);
pcl::PointXYZ v2(p3.x - p1.x, p3.y - p1.y, p3.z - p1.z);
// 计算两个向量的叉乘
pcl::PointXYZ cross_product;
cross_product.x = v1.y * v2.z - v1.z * v2.y;
cross_product.y = v1.z * v2.x - v1.x * v2.z;
cross_product.z = v1.x * v2.y - v1.y * v2.x;
// 如果叉乘结果为零向量,则说明三个点共线
return cross_product.x == 0 && cross_product.y == 0 && cross_product.z == 0;
}
//根据圆柱面参数创建空间任意圆柱面点云
//param[in] p1, p2, p3: 输入的三个空间点
//param[in] num_points:随机点的数量
//param[out] cloud:PCD格式的点云文件
pcl::PointCloud<pcl::PointXYZ>::Ptr generateTrianglePointCloud(const pcl::PointXYZ& p1, const pcl::PointXYZ& p2, const pcl::PointXYZ& p3, int num_points)
{
// 创建一个点云对象
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
// 填充三角形内的点
for (int i = 0; i < num_points; i++)
{
float u = static_cast<float>(rand()) / RAND_MAX; // 在[0, 1]范围内生成随机数
float v = static_cast<float>(rand()) / RAND_MAX; // 在[0, 1]范围内生成随机数
if (u + v > 1.0)
{
u = 1.0 - u;
v = 1.0 - v;
}
float w = 1.0 - u - v;
pcl::PointXYZ point;
point.x = u * p1.x + v * p2.x + w * p3.x;
point.y = u * p1.y + v * p2.y + w * p3.y;
point.z = u * p1.z + v * p2.z + w * p3.z;
cloud->push_back(point);
}
return cloud;
}
主函数代码如下
int main()
{
// 随机定义四个三维点
pcl::PointXYZ p1(1,4,7);
pcl::PointXYZ p2(3,3,3);
pcl::PointXYZ p3(8,3.2,0);
// 检查是否共线
if (arePointsCollinear(p1, p2, p3)) {
std::cout << "警告:三个点共线!" << std::endl;
return 0;
}
// 生成三角形面点云
pcl::PointCloud<pcl::PointXYZ>::Ptr triangle1_cloud = generateTrianglePointCloud(p1, p2, p3, 10000);
// 创建可视化对象并添加点云
pcl::visualization::PCLVisualizer viewer("Point Cloud Viewer");
viewer.setBackgroundColor(0, 0, 0);
viewer.addPointCloud<pcl::PointXYZ>(triangle1_cloud, "cloud");
// 保存点云数据
pcl::io::savePCDFileASCII("triangle1_cloud.pcd", *triangle1_cloud);
// 设置点云颜色为红色
viewer.setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 1.0, 0.0, 0.0, "cloud");
// 设置点云大小
viewer.setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 2, "cloud");
// 等待可视化窗口关闭
while (!viewer.wasStopped())
{
viewer.spinOnce();
}
return 0;
}
可视化结果如图
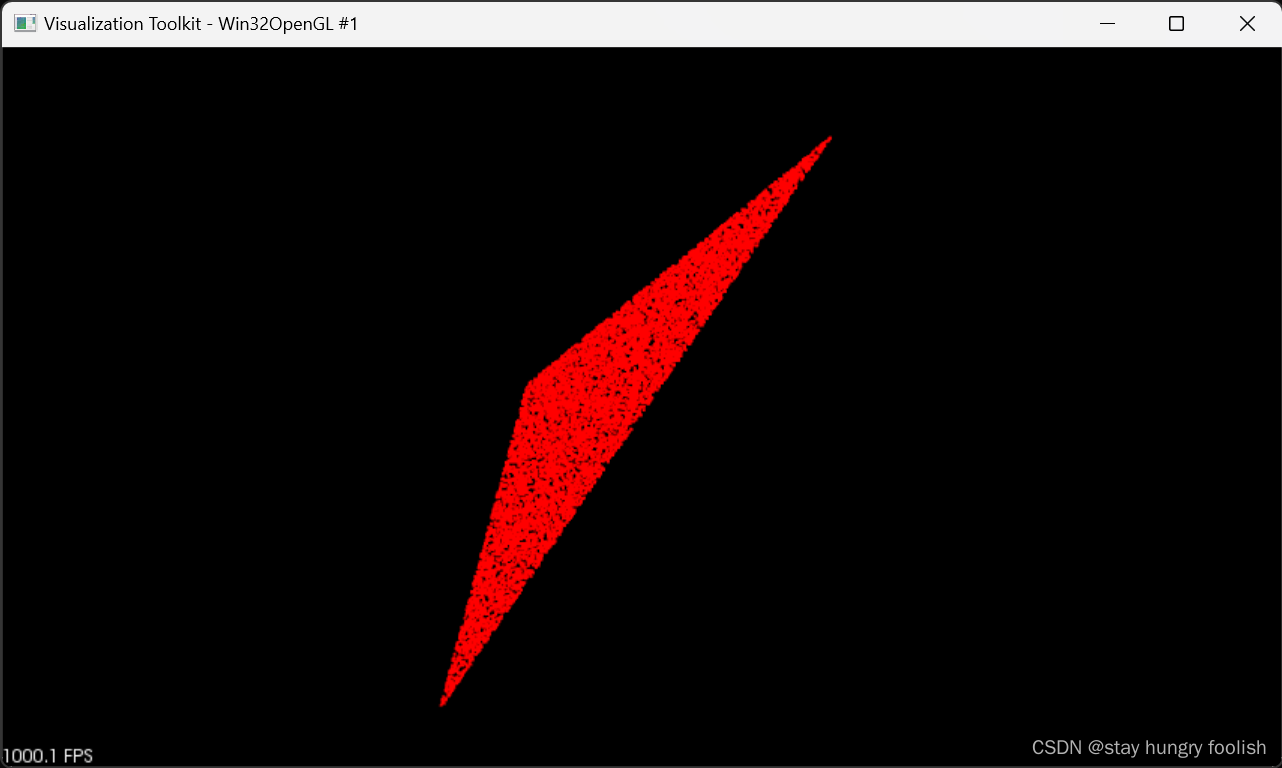
效果还不赖,觉得点太多或太少都可以自己设置点的数量~
总结
只要三个点不共线,就能创建与之对应的三角形面点云。如果有用记得三连哦,转载请注明出处!