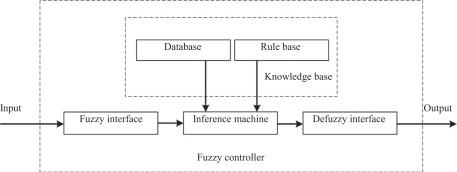
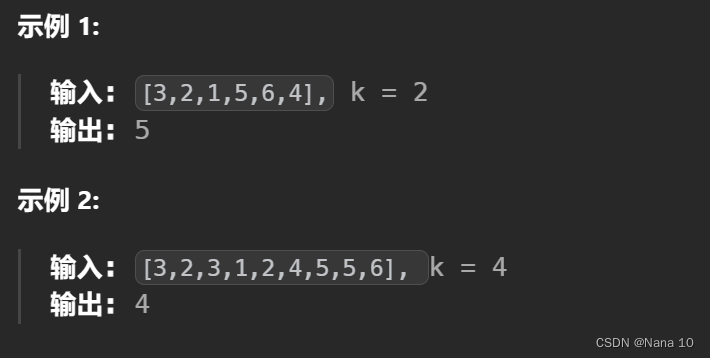
（1）215数组中的第k个最大元素–中等

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        //维护一个长度为k的堆，堆顶元素即为第k大的数
        // priority_queue<int>  //默认降序队列，大顶堆
        // priority_queue<int,vector<int>,less<int>> //降序队列，大顶堆
        // priority_queue<int,vector<int>,greater<int>>  //升序队列，小顶堆
        priority_queue<int, vector<int>, greater<int>> Q;
        for(int i = 0; i< nums.size(); i++){
            //前k个直接进入堆
            if(i<k) Q.push(nums[i]);
            //k+1个开始，维护最大的k个在堆中
            else if(nums[i] > Q.top()) {
                Q.pop();
                Q.push(nums[i]);
            }
        }return Q.top();
    }
};

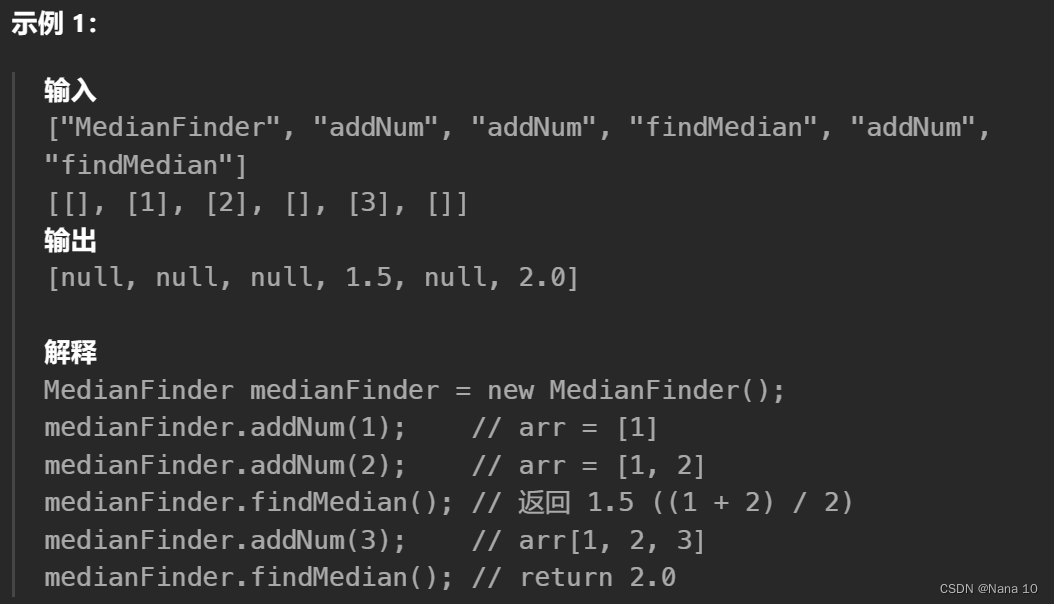
（2）295数据流的中位数–困难

中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。

例如 arr = [2,3,4] 的中位数是 3 。
例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。
实现 MedianFinder 类:

MedianFinder() 初始化 MedianFinder 对象。

void addNum(int num) 将数据流中的整数 num 添加到数据结构中。

double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。

class MedianFinder {

private:
    //维护两个堆
    //最大堆，较小的一半元素，堆顶为较大元素中的最小值
    priority_queue<int, vector<int>, less<int>> big_queue;
    //最小堆，放较大的一半元素,堆顶为较小元素中的最大值
    priority_queue<int, vector<int>, greater<int>> small_queue;

public:
    MedianFinder() {
        
    }
    
    void addNum(int num) {
        //如果两堆数量相等，选择相应的放即可
        if(big_queue.size() == small_queue.size()){
            if(big_queue.size() == 0) big_queue.push(num);
            else if(num <= big_queue.top()) big_queue.push(num);
            else small_queue.push(num);
        }
        //如果最大堆较多
        else if(big_queue.size()> small_queue.size()){
            //新元素属于较小的一半，需要插入最大堆
            if(num < big_queue.top()){
                //将最大堆堆顶移到最小堆中来
                small_queue.push(big_queue.top());
                big_queue.pop();
                //最大堆push进新元素
                big_queue.push(num);
            }
            //新元素属于较大的一半，需要插入最小堆
            else small_queue.push(num);
        }
        //如果最小堆较多
        else{
            //新元素属于较大的一半，需要插入最小堆
            if(num > small_queue.top()){
                //将最小堆堆顶移到最大堆中来
                big_queue.push(small_queue.top());
                small_queue.pop();
                //最小堆push进新元素
                small_queue.push(num);
            }
            //新元素属于较小的一半，需要插入最大堆
            else big_queue.push(num);
        }
    }
    
    double findMedian() {
        if(big_queue.size() == 0 && small_queue.size() == 0) return NULL;
        else if (big_queue.size() == small_queue.size()) return (big_queue.top()+small_queue.top())/2.0;
        else return (big_queue.size()>small_queue.size()?big_queue.top():small_queue.top());

    }
};

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */