论文解读者：胡明杰

编者按：

贝叶斯优化是一种处理黑盒函数优化的常用方法. 大多数的贝叶斯优化方法假设评估成本是同质的. 然而, 在实际问题中，评估成本往往是异质且未知的. 此外，现有的考虑异质评估成本的方法并不能很好地处理有约束的贝叶斯优化问题. 未知的评估成本和预算约束引入了新的探索和利用权衡(exploration-exploitation trade-off), 算法需要同时学习成本函数. 本文[1]证明了现有的方法期望提升（EI）和单位成本期望提升（EI-PUC）相比于最优的非短视最优策略可以表现得任意差. 为了克服现有方法的缺点，本文提出了带有预算约束的多步期望提升（B-MS-EI）方法，其是一种非短视的采样函数并将传统的EI推广到了异方差和未知评估成本的设定下. 最后，本文证明了提出的采样函数在一系列的合成和真实问题中的表现优于现有的方法.

1. 带有未知评估成本和预算约束的贝叶斯优化问题

给定一个紧的可行域$\mathbb{X}\subset {\mathbb{R}}^d$, 我们的目的是找到一个可行解$x\in \mathbb{X}$使得目标函数值最大. 目标函数$f:\mathbb{X}\to \mathbb{R}$是一个黑盒函数，每查询一个点$x$时只能得到函数值$f(x)$的一个带有噪声的观测值. 设查询的点列为 { x i } i = 1 n \{x_i\}_{i=1}^{n} {xi​}i=1n​，其需要满足预算约束${\sum }_{i=1}^{n}c(x_i)\le B$. 其中$c(x)$表示评估$x$点处函数值的成本，$B$是总的评估预算. 每次查询，可以得到函数值$f(x)$和成本函数$c(x)$带噪声的观测值. 假设 $f$和 $c$的联合先验分布为$p$. 一个观测值表示为 $(x_i,y_i,z_i)\in \mathbb{X}\times \mathbb{R}\times {\mathbb{R}}_{>0}$, 其中 $y_i$和 $z_i$分别是目标函数和成本函数在 $x_i$处的观测值.

1.1 MDP 建模

我们将上述问题建模为一个多阶段的随机动态规划问题(MDP). 状态 ${\mathcal{D}}_n$定义为当前的观测值集合，对于 $n\ge 1$, ${\mathcal{D}}_n={\mathcal{D}}_{n-1}\cup (x_n,y_n,z_n)$. ${\mathcal{D}}_0$表示初始的观测值集合. 给定 ${\mathcal{D}}_n$,$f$和 $c$的联合后验分布表示为 $p(\cdot |{\mathcal{D}}_n)$. 状态${\mathcal{D}}_n$产生的效用定义为最大观测的函数值 μ ( D n ) = m a x { x , y , x } ∈ D n y \mu(\mathcal{D}_n)=max_{\{x,y,x\}\in{\mathcal{D}_n}}y μ(Dn​)=max{x,y,x}∈Dn​​y. 令 $s({\mathcal{D}}_n)={\sum }_{(x,y,z)\in {\mathcal{D}}_n}z$表示 ${\mathcal{D}}_n$中观测值的总成本.

由于包含尚未观测到的目标函数值和成本函数值， ${\mathcal{D}}_1,{\mathcal{D}}_2,...$是随机变量. 策略 π = { π k } k = 1 ∞ \pi=\{\pi_k\}_{k=1}^{\infty} π={πk​}k=1∞​是一个函数序列，每个函数将观测值的集合映射到 $\mathbb{X}$中的点，即 $x_k={\pi }_k({\mathcal{D}}_{k-1})$. 给定观测值的集合 $\mathcal{D}$满足 $s(D)\le B$, 策略 $\pi $的价值函数定义为 $V^{\pi }(\mathcal{D})={\mathbb{E}}^{\pi }[\mu ({\mathcal{D}}_{N_B})-\mu ({\mathcal{D}}_0)|{\mathcal{D}}_0=\mathcal{D}]$, 其中随机停时 N B = sup ⁡ { k : s ( D k ) ≤ B } N_B=\sup\{k:s(\mathcal{D}_k)\leq B\} NB​=sup{k:s(Dk​)≤B}是满足预算约束的前提下最大的时间步长$k$. 对于满足 $s(\mathcal{D})\ge B$的观测值集合 $\mathcal{D}$，定义 $V^{\pi }(\mathcal{D})=0$. 我们的目标是找到一个策略 $\pi$最大化期望效用：
$$\begin{array}{c}{V}^{\ast }(\mathcal{D})=\underset{\pi \in \prod }{\sup }{V}^{\pi }(\mathcal{D})\end{array}$$

其中， $\prod$是所有可能的策略集合. 由于 $N_B$是一个随机变量，问题（1）可以看作一个随机的最短路径规划问题. 这样建模的好处在于：第一，通过多步规划，可以权衡高成本和低成本之间的评估，从而更好地利用给定的预算. 第二，它可以处理最优成本学习(cost learning)时的不确定性. 比如说：一个探索性的评估适合在中等的预测成本和很高的模型不确定区域进行.

1.2 和成本价值比方法的不同

定理1：
EI和EI-PUC策略得到的近似比是无界的，也就是说对于任意大的 $\rho >0$和策略 p i ∈ { EI,EI-PUC } pi \in \{\text{EI,EI-PUC}\} pi∈{EI,EI-PUC},存在一个贝叶斯优化的问题实例使得 $$V^{\ast }({\mathcal{D}}_0)>\rho V^{\pi }({\mathcal{D}}_0)(2)$$

定理1的证明可以通过构建一个贝叶斯优化的问题实例, 该实例中包含两类点: 高成本的点且带有很大的先验方差以及低成本的点带有较小的方差. 低成本点的方差足够小以至于在期望意义下, 将整个预算用于评估它们所获得的价值仅是评估单个高成本点所获得价值的一小部分. 然而, EI-PUC会将所有的预算花费在低成本, 低方差的点上导致获得的价值很少. 相反, 最优策略将其全部预算用于对高成本点的一次评估，从而获得更大的期望价值.

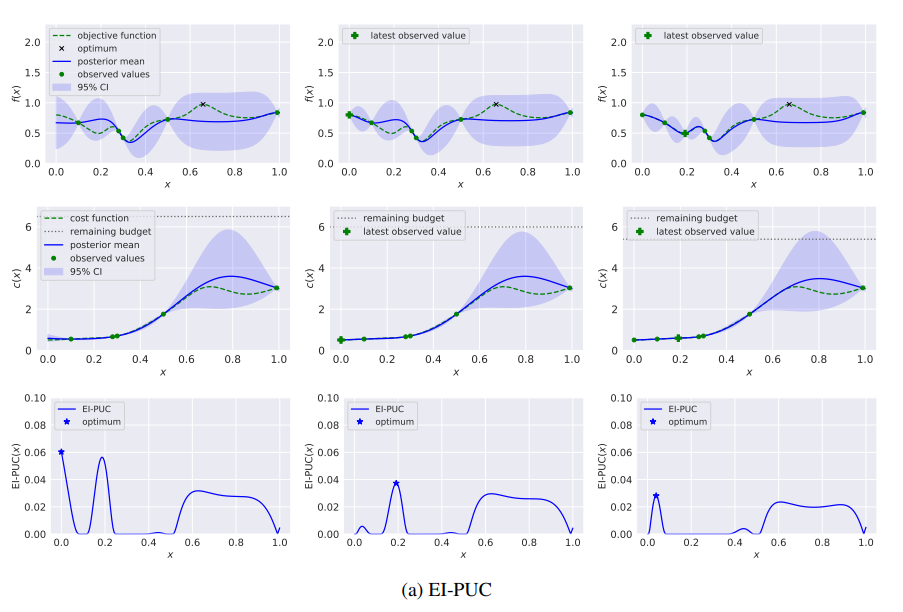
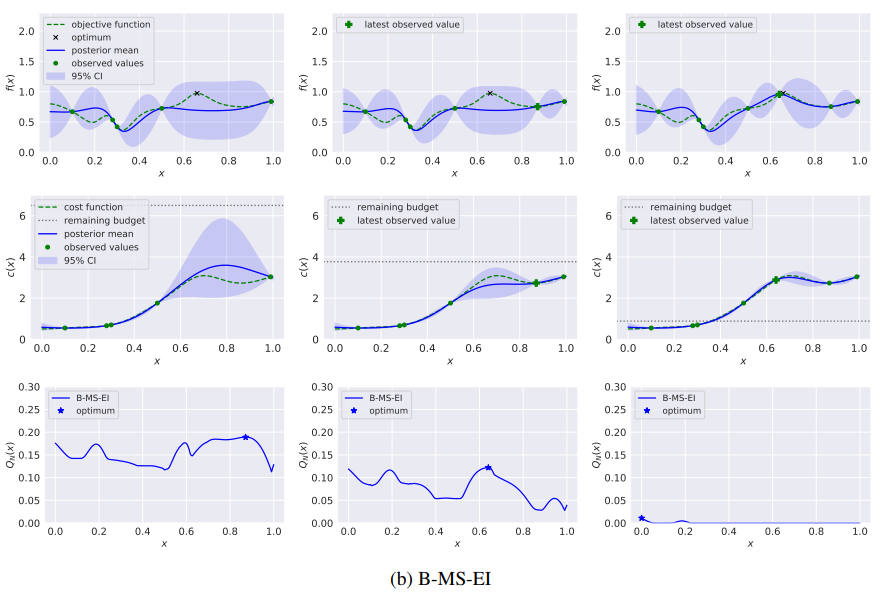
下图通过一个具有高斯过程先验的一维连续函数的例子说明了这种现象. 在第一个时间切片的后验下, 左侧有一个低成本区域(x < 0.5), 方差低, 平均值明显低于观察到的最佳点. 右边有一个成本较高的区域(x > 0.5)，其中均值和方差都较大. 这些均值和方差使得函数的全局最大值很可能在右侧区域. 在前两次评估中, EI-PUC策略在两个低成本点进行评估, 这导致该区域的方差减少, 但(如预期的那样)没有值与右侧的全局最大值的可能值相抗衡. 相比之下, 在前两次评估中, 本文的多步B-MS-EI策略在右侧进行评估, 找到接近全局最优的值.

1.3 分解和截断

令 $r({\mathcal{D}}_{n-1},{\mathcal{D}}_n)=\mu ({\mathcal{D}}_n)-\mu ({\mathcal{D}}_{n-1})$表示连续的状态之间效用的提升, 我们有：
V ∗ ( D ) = sup ⁡ π ∈ Π E π [ ∑ n = 1 ∞ r ( D n − 1 , D n ) 1 { n ≤ N B } ∣ D 0 = D ] ( 3 ) \qquad \qquad \qquad V^*(\mathcal{D})=\sup _{\pi \in \Pi} \mathbb{E}^\pi\left[\sum_{n=1}^{\infty} r\left(\mathcal{D}_{n-1}, \mathcal{D}_n\right) \mathbf{1}_{\left\{n \leq N_B\right\}} \mid \mathcal{D}_0=\mathcal{D}\right] \qquad \qquad \qquad \qquad (3) V∗(D)=π∈Πsup​Eπ[n=1∑∞​r(Dn−1​,Dn​)1{n≤NB​}​∣D0​=D](3)
对问题（2）截断处理后可以得到：
V N ( D ) = sup ⁡ π ∈ Π E π [ ∑ n = 1 N r ( D n − 1 , D n ) 1 { n ≤ N B } ∣ D 0 = D ] ( 4 ) \qquad \qquad \qquad V_N(\mathcal{D})=\sup _{\pi \in \Pi} \mathbb{E}^\pi\left[\sum_{n=1}^N r\left(\mathcal{D}_{n-1}, \mathcal{D}_n\right) \mathbf{1}_{\left\{n \leq N_B\right\}} \mid \mathcal{D}_0=\mathcal{D}\right] \qquad \qquad \qquad \qquad (4) VN​(D)=π∈Πsup​Eπ[n=1∑N​r(Dn−1​,Dn​)1{n≤NB​}​∣D0​=D](4)

其中, $N$是固定的“向前看”的步数且 ${\lim }_{N\to \infty }{V}_N(\mathcal{D})=V^{\ast }(\mathcal{D})$.

2.有预算的多步EI方法

我们现在来推导有预算的多步期望提升（B-MS-EI）方法, 主要的想法是求解截断后的问题（4）. 因此，采样函数是带有参数$N$的, 即最大的向前看的步数.

2.1 动态规划求解截断的动态规划问题

定义在给定观测值集合 $\mathcal{D}$的条件下评估点$x$的一步边际报酬为：
Q 1 ( x ∣ D ) = E y , z [ r ( D , D ∪ { ( x , y , z ) } ) 1 { s ( D ) + z ≤ B } ] = E y , z [ ( y − u ( D ) ) + 1 { s ( D ) + z ≤ B } ] ( 5 ) Q_1(x \mid \mathcal{D})=\mathbb{E}_{y, z}\left[r(\mathcal{D}, \mathcal{D} \cup\{(x, y, z)\}) \mathbf{1}_{\{s(\mathcal{D})+z \leq B\}}\right]=\mathbb{E}_{y, z}\left[(y-u(\mathcal{D}))^{+} \mathbf{1}_{\{s(\mathcal{D})+z \leq B\}}\right] \qquad \qquad (5) Q1​(x∣D)=Ey,z​[r(D,D∪{(x,y,z)})1{s(D)+z≤B}​]=Ey,z​[(y−u(D))+1{s(D)+z≤B}​](5)

定义在给定观测值集合 $\mathcal{D}$的条件下评估点$x$的一步边际报酬为：
Q 1 ( x ∣ D ) = E y , z [ r ( D , D ∪ { ( x , y , z ) } ) 1 { s ( D ) + z ≤ B } ] = E y , z [ ( y − u ( D ) ) + 1 { s ( D ) + z ≤ B } ] ( 5 ) Q_1(x \mid \mathcal{D})=\mathbb{E}_{y, z}\left[r(\mathcal{D}, \mathcal{D} \cup\{(x, y, z)\}) \mathbf{1}_{\{s(\mathcal{D})+z \leq B\}}\right]=\mathbb{E}_{y, z}\left[(y-u(\mathcal{D}))^{+} \mathbf{1}_{\{s(\mathcal{D})+z \leq B\}}\right] \qquad \qquad (5) Q1​(x∣D)=Ey,z​[r(D,D∪{(x,y,z)})1{s(D)+z≤B}​]=Ey,z​[(y−u(D))+1{s(D)+z≤B}​](5)

引理1：假设$f$和$\ln c$服从高斯过程先验分布且$\mathcal{D}$是任意的观测值集合。定义 ${\mu }_D^f(x)=\mathbb{E}[f(x)|\mathcal{D}]$，${\mu }_D^{\ln c}(x)=\mathbb{E}[\ln c(x)|\mathcal{D}]$, ${\sigma }_D^f(x)=Var[f(x)|\mathcal{D}{]}^{\frac{1}{2}}$和 ${\sigma }_{\mathcal{D}}^{\ln c}=Var[\ln c(x)|\mathcal{D}{]}^{\frac{1}{2}}$. 那么我们有：
$$Q_1(x|\mathcal{D})=E{I}^f(x|\mathcal{D})\varphi (\zeta )1_{s(\mathcal{D})\le B}(6)$$

其中,$E{I}^f$是经典的对$f$的期望提升， $\zeta =(\ln (B-s(\mathcal{D}))-{\mu }_{\mathcal{D}}^{\ln c}(x))/{\sigma }_{\mathcal{D}}^{\ln c}(x)$, 且 $\varphi$是标准正态分布的cdf.

类似的，我们可以定义在 $x$处进行评估的 $n$步价值函数：
$$Q_n(x\mid \mathcal{D})=Q_1(x\mid \mathcal{D})+{\mathbb{E}}_{y,z}\left[\underset{x\in \mathbb{X}}{\max }{Q}_{n-1}(x\mid \mathcal{D}\cup \{(x,y,z)\})\right](7)$$
我们的多步期望提升采样函数定义为 $Q_N$, 意味着在每一步我们的评估策略在$x_{n+1}\in \arg {\max }_{x\in \mathbb{X}}{Q}_N(x|{\mathcal{D}}_n)$处采样.

类似的，我们可以定义在 $x$处进行评估的 $n$步价值函数：
$$Q_n(x\mid \mathcal{D})=Q_1(x\mid \mathcal{D})+{\mathbb{E}}_{y,z}\left[\underset{x\in \mathbb{X}}{\max }{Q}_{n-1}(x\mid \mathcal{D}\cup \{(x,y,z)\})\right](7)$$
我们的多步期望提升采样函数定义为 $Q_N$, 意味着在每一步我们的评估策略在$x_{n+1}\in \arg {\max }_{x\in \mathbb{X}}{Q}_N(x|{\mathcal{D}}_n)$处采样.

2.2 利用一次多步树(One-shot Multi-Step Trees)优化采样函数

优化B-MS-EI采样函数需要求解一个连续的嵌套随机优化问题，这是相当具有挑战性的. 本文在多步情景树方法[2]的基础上基于求解 ${\max }_{x\in \mathbb{X}}{Q}_N(x|{\mathcal{D}}_n)$的样本平均近似(Sample Average Approximation) 得到了一个优化方法. 每一个情景对应自己的一个决策变量, 从而将问题转化为一个定义域维度更高的确定性优化问题. 本文利用自动微分和批量线性代数运算的工具来解决该高维的优化问题. 通过重复利用贝尔曼迭代, $Q_N$可以写为：
Q N ( x ∣ D ) = Q 1 ( x ∣ D ) + E y , z [ max ⁡ x 2 { Q 1 ( x 2 ∣ D 1 ) + E y , z [ max ⁡ x 3 { Q 1 ( x 3 ∣ D 2 ) + ⋯   } ] } ] ( 8 ) Q_N(x \mid \mathcal{D})=Q_1(x \mid \mathcal{D})+\mathbb{E}_{y, z}\left[\max _{x_2}\left\{Q_1\left(x_2 \mid \mathcal{D}_1\right)+\mathbb{E}_{y, z}\left[\max _{x_3}\left\{Q_1\left(x_3 \mid \mathcal{D}_2\right)+\cdots\right\}\right]\right\}\right] \qquad \qquad (8) QN​(x∣D)=Q1​(x∣D)+Ey,z​[x2​max​{Q1​(x2​∣D1​)+Ey,z​[x3​max​{Q1​(x3​∣D2​)+⋯}]}](8)

现在，我们考虑$Q_N(x|\mathcal{D})$的蒙特卡洛近似：
$$\begin{array}{rl}& {\hat{Q}}_N(x\mid \mathcal{D})\\ =& Q_1(x\mid \mathcal{D})+\frac{1}{m_1}\sum _{j_1}^{m_1}\left[\underset{x_2^{j_1}}{\max }\left\{Q_1\left(x_2^{j_1}\mid {\mathcal{D}}_1^{j_1}\right)+\frac{1}{m_2}\sum _{j_2}^{m_2}\left[\underset{x_3^{j_1{j}_2}}{\max }\left\{Q_1\left(x_3^{j_1{j}_2}\mid {\mathcal{D}}_2^{j_1{j}_2}\right)+\cdots \right\}\right]\right\}\right]\end{array}(9)$$

其中，$m_i,i=1,...,N-1$是第$i$步使用的样本数, 观测值的集合通过方程 ${\mathcal{D}}_i^{j_1}=\mathcal{D}\cup \{(x,y_i^{j_1},z_i^{j_1})\}$递归地定义.

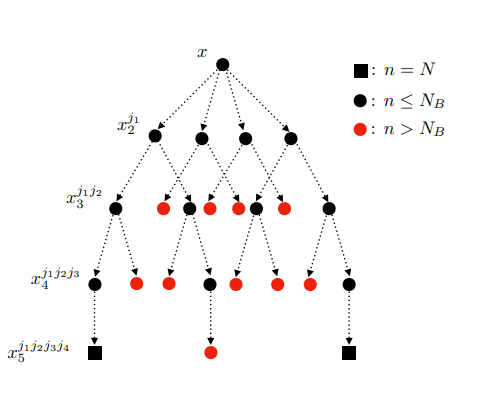
2.3通过基本抽样策略推出的预算调度

令 $B_n=B-{\sum }_{i=1}^n{z}_i$表示$n$时剩余的预算数, 由于计算量的限制, 在实际中可以执行的向前看步骤的数量(N)相对较少, $B_n$可能太大了, 我们的采样函数无法很好地考虑成本的影响, 尤其是在最初的几次评估中. 因此，在本文的方法中, 令采样函数在步骤n中不使用实际的剩余预算, 而是使用由启发式规则设置的幻想预算(fantasy budget). 本文提出了一种启发式预算调度规则，该规则基于一个计算快速的基本抽样策略. 设想在这个基本抽样策略下进行 $N$次顺序评估. 更具体地说，对于 $N$个步骤中的每一步，使用(联合)后验分布在该策略建议的点上计算幻想目标和成本值，然后通过合并这些幻想评估来更新后验分布，并重复. 由此产生的 $N$个幻想成本的总和决定了基本抽样策略产生的累积成本. 然后，将采样函数的预算设置为累积成本与真实剩余预算之间的最小值.该方法将此预算当作实际预算来使用，直到耗尽为止，然后再次使用启发式规则来计算新的幻想预算.

3.数值实验

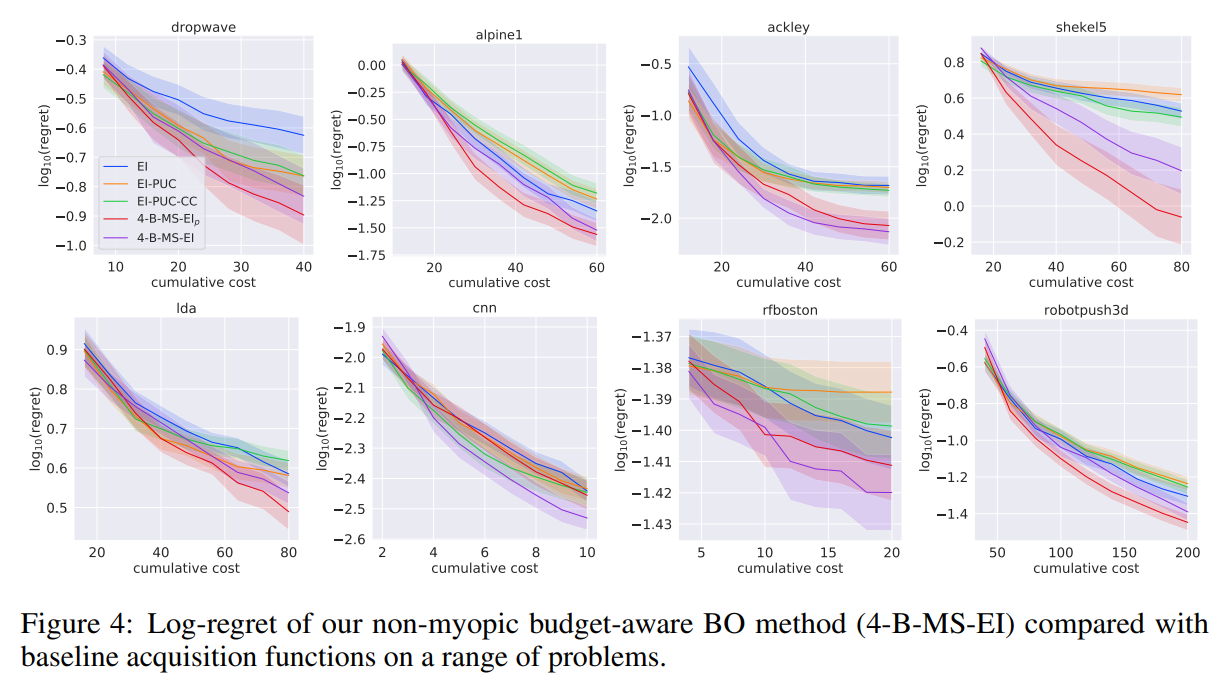
本文在四个合成实验和四个实际实验中证明了B-MS-EI的有效性并报告了采样函数B-MS-EI的两个变体: $\text{N-B-MS-EI}$, ${\text{N-B-MS-EI}}_p$的性能. 此外，我们报告了三个基线采集函数的性能： $\text{EI},\text{EI-PUC},\text{EI-PUC-CC}$.

下图绘制了平均对数后悔率与当前使用的预算的95%置信区间. 与现有方法相比，B-MS-EI(红色和紫色线)表现良好，具体实验细节参见原文.

参考文献

[1] Astudillo R, Jiang D, Balandat M, et al. Multi-step budgeted bayesian optimization with unknown evaluation costs[J]. Advances in Neural Information Processing Systems, 2021, 34: 20197-20209.
[2] Jiang S, Jiang D, Balandat M, et al. Efficient nonmyopic bayesian optimization via one-shot multi-step trees[J]. Advances in Neural Information Processing Systems, 2020, 33: 18039-18049.