本文仅供学习使用
本文参考:
《变分法基础-第三版》老大中
《变分学讲义》张恭庆
《Calculus of Variations of Optimal Control Theory》-变分法和最优控制论-Daneil Liberzon
Ch01-2 数学基础-预备知识1
- 1.3.2 向量场的通量和散度
- 1.3.3 高斯定理与格林公式
1.3.2 向量场的通量和散度
设有向量场 a ⃗ \vec{a} a,在场内取一有向曲面 S S S, d S dS dS是 S S S上的曲面元素,在 d S dS dS任取一点 M M M, n ⃗ \vec{n} n是点 M M M处外法向方向的单位向量,若将 a ⃗ ⋅ n ⃗ d S \vec{a}\cdot \vec{n}\mathrm{d}S a⋅ndS对曲面 S S S积分:
Φ = ∬ S a ⃗ ⋅ d S ⃗ = ∬ S a ⃗ ⋅ n ⃗ d S = ∬ S a n d S \varPhi =\iint_S{\vec{a}\cdot \mathrm{d}\vec{S}}=\iint_S{\vec{a}\cdot \vec{n}}\mathrm{d}S=\iint_S{a_n}\mathrm{d}S Φ=∬Sa⋅dS=∬Sa⋅ndS=∬SandS
则 φ \varphi φ称为向量 a ⃗ \vec{a} a沿外法线向量 n ⃗ \vec{n} n的方向通过曲面 S S S的通量。
曲面
S
S
S在三个坐标面上的投影分别为:
{
d
y
d
z
=
cos
(
N
⃗
,
x
)
d
S
⃗
=
cos
α
d
S
⃗
=
l
d
S
⃗
d
z
d
x
=
cos
(
N
⃗
,
y
)
d
S
⃗
=
cos
β
d
S
⃗
=
m
d
S
⃗
d
x
d
y
=
cos
(
N
⃗
,
z
)
d
S
⃗
=
cos
γ
d
S
⃗
=
n
d
S
⃗
\begin{cases} \mathrm{d}y\mathrm{d}z=\cos \left( \vec{N},x \right) \mathrm{d}\vec{S}=\cos \alpha \mathrm{d}\vec{S}=l\mathrm{d}\vec{S}\\ \mathrm{d}z\mathrm{d}x=\cos \left( \vec{N},y \right) \mathrm{d}\vec{S}=\cos \beta \mathrm{d}\vec{S}=m\mathrm{d}\vec{S}\\ \mathrm{d}x\mathrm{d}y=\cos \left( \vec{N},z \right) \mathrm{d}\vec{S}=\cos \gamma \mathrm{d}\vec{S}=n\mathrm{d}\vec{S}\\ \end{cases}
⎩
⎨
⎧dydz=cos(N,x)dS=cosαdS=ldSdzdx=cos(N,y)dS=cosβdS=mdSdxdy=cos(N,z)dS=cosγdS=ndS
有向曲面 d S ⃗ \mathrm{d}\vec{S} dS可表示为: d S ⃗ = n ⃗ d S = i ⃗ d y d z + j ⃗ d z d x + k ⃗ d x d y \mathrm{d}\vec{S}=\vec{n}\mathrm{d}S=\vec{i}\mathrm{d}y\mathrm{d}z+\vec{j}\mathrm{d}z\mathrm{d}x+\vec{k}\mathrm{d}x\mathrm{d}y dS=ndS=idydz+jdzdx+kdxdy
向量
a
⃗
\vec{a}
a通过曲面
S
S
S的通量还可以写成以下形式:
Φ
=
∯
S
[
a
x
cos
(
N
⃗
,
x
)
+
a
y
cos
(
N
⃗
,
y
)
+
a
z
cos
(
N
⃗
,
z
)
]
d
S
⃗
=
∯
S
(
a
x
d
y
d
z
+
a
y
d
z
d
x
+
a
z
d
x
d
y
)
\varPhi =\oiint_S{\left[ a_x\cos \left( \vec{N},x \right) +a_{\mathrm{y}}\cos \left( \vec{N},y \right) +a_{\mathrm{z}}\cos \left( \vec{N},z \right) \right]}\mathrm{d}\vec{S} \\ =\oiint_S{\left( a_x\mathrm{d}y\mathrm{d}z+a_{\mathrm{y}}\mathrm{d}z\mathrm{d}x+a_{\mathrm{z}}\mathrm{d}x\mathrm{d}y \right)}
Φ=∬S[axcos(N,x)+aycos(N,y)+azcos(N,z)]dS=∬S(axdydz+aydzdx+azdxdy)
当曲面
S
S
S是封闭曲面时,具有特别重要的意义。为了明显起见,采用在积分号上加圆圈的方法,即用:
Φ
=
∯
S
a
n
d
S
=
∯
S
a
⃗
d
S
⃗
\varPhi =\oiint_S{a_{\mathrm{n}}}\mathrm{d}S=\oiint_S{\vec{a}}\mathrm{d}\vec{S}
Φ=∬SandS=∬SadS
来表示通过封闭曲面
S
S
S的通量。
设有向量场 a ⃗ = a ⃗ ( M ) \vec{a}=\vec{a}\left( M \right) a=a(M) ,在场中一点 M M M的某个邻域内作包含此点的任一封闭曲面 Δ S \varDelta S ΔS, Δ S \varDelta S ΔS所围成的体积为 Δ V \varDelta V ΔV,计算向量 a ⃗ \vec{a} a穿过 Δ S \varDelta S ΔS面上的通量,当 Δ V \varDelta V ΔV以任意方式向点 M M M收缩时,如果比式:
lim Δ V → 0 Δ Φ Δ V = lim Δ V → 0 ∯ Δ S a ⃗ ⋅ d S ⃗ Δ V \underset{\varDelta V\rightarrow 0}{\lim}\frac{\varDelta \varPhi}{\varDelta V}=\underset{\varDelta V\rightarrow 0}{\lim}\frac{\oiint_{\varDelta S}{\vec{a}\cdot}\mathrm{d}\vec{S}}{\varDelta V} ΔV→0limΔVΔΦ=ΔV→0limΔV∬ΔSa⋅dS
的极限存在,则此极限称为向量函数 a ⃗ \vec{a} a在点 M M M的散度,记作 d i v a ⃗ \mathrm{div}\vec{a} diva, d i v \mathrm{div} div为英文divergence的缩写,意为散度。当采用哈密顿算子时,可写作 ∇ ⋅ a ⃗ \nabla \cdot \vec{a} ∇⋅a,即:
d i v a ⃗ = ∇ ⋅ a ⃗ = lim Δ V → 0 Δ Φ Δ V = lim Δ V → 0 ∯ Δ S a ⃗ ⋅ d S ⃗ Δ V ∇ ⋅ a ⃗ \mathrm{div}\vec{a}=\nabla \cdot \vec{a}=\underset{\varDelta V\rightarrow 0}{\lim}\frac{\varDelta \varPhi}{\varDelta V}=\underset{\varDelta V\rightarrow 0}{\lim}\frac{\oiint_{\varDelta S}{\vec{a}\cdot}\mathrm{d}\vec{S}}{\varDelta V} \\ \nabla \cdot \vec{a} diva=∇⋅a=ΔV→0limΔVΔΦ=ΔV→0limΔV∬ΔSa⋅dS∇⋅a
显然点M的散度与所取的封闭曲面 Δ S \varDelta S ΔS的形状无关,它是一个不依赖于坐标系选取的数量,因此是一个标量。散度是通量对体积的变化率。散度为零的向量场称为无源场或无散场,也称为管状场。
虽然向量场的散度是一个不依赖于坐标系选取的标量,但在具体计算向量场的散度时,常需要用向量的分量来表示,而向量的分量和坐标的选择有关。因此需要讨论向量的散度与其分量的关系。
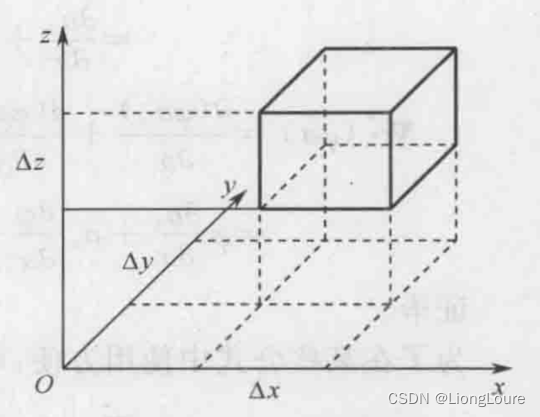
设直角坐标系向量:
a
⃗
=
a
x
i
⃗
+
a
y
j
⃗
+
a
z
k
⃗
\vec{a}=a_x\vec{i}+a_{\mathrm{y}}\vec{j}+a_{\mathrm{z}}\vec{k}
a=axi+ayj+azk,微元体积
Δ
V
\varDelta V
ΔV是以
Δ
x
\varDelta x
Δx、
Δ
y
\varDelta y
Δy和
Δ
z
\varDelta z
Δz为边长的微元六面体,并设微元六面体的中心坐标为
(
x
,
y
,
z
)
\left( x,y,z \right)
(x,y,z)。作为一阶近似,在
x
x
x方向存在如下关系:
a
x
∣
x
+
Δ
x
2
=
a
x
∣
x
+
∂
a
x
∂
x
Δ
x
2
,
a
x
∣
x
−
Δ
x
2
=
a
x
∣
x
−
∂
a
x
∂
x
Δ
x
2
\left. a_x \right|_{x+\frac{\varDelta x}{2}}=\left. a_x \right|_x+\frac{\partial a_x}{\partial x}\frac{\varDelta x}{2},\left. a_x \right|_{x-\frac{\varDelta x}{2}}=\left. a_x \right|_x-\frac{\partial a_x}{\partial x}\frac{\varDelta x}{2}
ax∣x+2Δx=ax∣x+∂x∂ax2Δx,ax∣x−2Δx=ax∣x−∂x∂ax2Δx
在
x
x
x轴方向流出微元六面体的净通量为:
(
a
x
∣
x
+
Δ
x
2
−
a
x
∣
x
−
Δ
x
2
)
Δ
y
Δ
z
=
∂
a
x
∂
x
Δ
x
Δ
y
Δ
z
\left( \left. a_x \right|_{x+\frac{\varDelta x}{2}}-\left. a_x \right|_{x-\frac{\varDelta x}{2}} \right) \varDelta y\varDelta z=\frac{\partial a_x}{\partial x}\varDelta x\varDelta y\varDelta z
(ax∣x+2Δx−ax∣x−2Δx)ΔyΔz=∂x∂axΔxΔyΔz
同样,在
y
y
y轴和
z
z
z轴方向也可以到类似的关系,于是流出微元体积
Δ
V
\varDelta V
ΔV的净通量为:
∯
Δ
z
a
⃗
⋅
d
S
⃗
=
∂
a
x
∂
x
Δ
x
Δ
y
Δ
z
+
∂
a
y
∂
y
Δ
x
Δ
y
Δ
z
+
∂
a
z
∂
z
Δ
x
Δ
y
Δ
z
\oiint_{\varDelta z}{\vec{a}\cdot}\mathrm{d}\vec{S}=\frac{\partial a_x}{\partial x}\varDelta x\varDelta y\varDelta z+\frac{\partial a_{\mathrm{y}}}{\partial y}\varDelta x\varDelta y\varDelta z+\frac{\partial a_{\mathrm{z}}}{\partial z}\varDelta x\varDelta y\varDelta z
∬Δza⋅dS=∂x∂axΔxΔyΔz+∂y∂ayΔxΔyΔz+∂z∂azΔxΔyΔz
将上式两端除以微元体积
Δ
V
=
Δ
x
Δ
y
Δ
z
\varDelta V=\varDelta x\varDelta y\varDelta z
ΔV=ΔxΔyΔz并取极限,得:
d
i
v
a
⃗
=
lim
Δ
V
→
0
∯
Δ
z
a
⃗
⋅
d
S
⃗
Δ
V
=
∂
a
x
∂
x
+
∂
a
y
∂
y
+
∂
a
z
∂
z
\mathrm{div}\vec{a}=\underset{\varDelta V\rightarrow 0}{\lim}\frac{\oiint_{\varDelta z}{\vec{a}\cdot}\mathrm{d}\vec{S}}{\varDelta V}=\frac{\partial a_x}{\partial x}+\frac{\partial a_{\mathrm{y}}}{\partial y}+\frac{\partial a_{\mathrm{z}}}{\partial z}
diva=ΔV→0limΔV∬Δza⋅dS=∂x∂ax+∂y∂ay+∂z∂az
又:
∇
⋅
a
⃗
=
(
∂
∂
x
i
⃗
+
∂
∂
y
j
⃗
+
∂
∂
z
k
⃗
)
⋅
(
a
x
i
⃗
+
a
y
j
⃗
+
a
z
k
⃗
)
=
∂
a
x
∂
x
+
∂
a
y
∂
y
+
∂
a
z
∂
z
\nabla \cdot \vec{a}=\left( \frac{\partial}{\partial x}\vec{i}+\frac{\partial}{\partial y}\vec{j}+\frac{\partial}{\partial z}\vec{k} \right) \cdot \left( a_x\vec{i}+a_{\mathrm{y}}\vec{j}+a_{\mathrm{z}}\vec{k} \right) =\frac{\partial a_x}{\partial x}+\frac{\partial a_{\mathrm{y}}}{\partial y}+\frac{\partial a_{\mathrm{z}}}{\partial z}
∇⋅a=(∂x∂i+∂y∂j+∂z∂k)⋅(axi+ayj+azk)=∂x∂ax+∂y∂ay+∂z∂az
故:
d
i
v
a
⃗
=
∇
⋅
a
⃗
=
∂
a
x
∂
x
+
∂
a
y
∂
y
+
∂
a
z
∂
z
\mathrm{div}\vec{a}=\nabla \cdot \vec{a}=\frac{\partial a_x}{\partial x}+\frac{\partial a_{\mathrm{y}}}{\partial y}+\frac{\partial a_{\mathrm{z}}}{\partial z}
diva=∇⋅a=∂x∂ax+∂y∂ay+∂z∂az
上式就是散度在直角坐标系中的表达式。在计算向量场的散度时,应用该式通常要比直接引用定义式更方便。一个向量函数a的散度是一个标量函数。在向量场中任一点,向量
a
⃗
\vec{a}
a的散度等于它在各坐标轴上的分量对各自坐标变量的偏导数之和。
散度具有下列性质:
- 两个向量函数之和的散度等于各向量函数的散度之和
d i v ( a ⃗ + b ⃗ ) = d i v a ⃗ + d i v b ⃗ ∇ ⋅ ( a ⃗ + b ⃗ ) = ∇ ⋅ a ⃗ + ∇ ⋅ b ⃗ \mathrm{div}\left( \vec{a}+\vec{b} \right) =\mathrm{div}\vec{a}+\mathrm{div}\vec{b} \\ \nabla \cdot \left( \vec{a}+\vec{b} \right) =\nabla \cdot \vec{a}+\nabla \cdot \vec{b} div(a+b)=diva+divb∇⋅(a+b)=∇⋅a+∇⋅b- 数量函数与向量函数之积的散度等于数量函数与向量函数的散度之积加上数量函数的梯度与向量函数之内积
d i v ( φ a ⃗ ) = φ d i v a ⃗ + a ⃗ ⋅ g r a d φ ∇ ⋅ ( φ a ⃗ ) = φ ∇ ⋅ a ⃗ + a ⃗ ⋅ ∇ φ \mathrm{div}\left( \varphi \vec{a} \right) =\varphi \mathrm{div}\vec{a}+\vec{a}\cdot \mathrm{grad}\varphi \\ \nabla \cdot \left( \varphi \vec{a} \right) =\varphi \nabla \cdot \vec{a}+\vec{a}\cdot \nabla \varphi \\ div(φa)=φdiva+a⋅gradφ∇⋅(φa)=φ∇⋅a+a⋅∇φ证明:(待补充)
求梯度的散度: ∇ ⋅ ∇ ( φ ψ ) \nabla \cdot \nabla \left( \varphi \psi \right) ∇⋅∇(φψ)
∇ ⋅ ∇ ( φ ψ ) = ∇ ⋅ ( φ ∇ ψ + ψ ∇ φ ) = φ ∇ ⋅ ∇ ψ + ∇ φ ⋅ ∇ ψ + ψ ∇ ⋅ ∇ φ + ∇ ψ ⋅ ∇ φ = φ ∇ 2 ψ + 2 ∇ φ ⋅ ∇ ψ + ψ ∇ 2 φ = φ Δ ψ + 2 ∇ φ ⋅ ∇ ψ + ψ Δ φ \nabla \cdot \nabla \left( \varphi \psi \right) =\nabla \cdot \left( \varphi \nabla \psi +\psi \nabla \varphi \right) =\varphi \nabla \cdot \nabla \psi +\nabla \varphi \cdot \nabla \psi +\psi \nabla \cdot \nabla \varphi +\nabla \psi \cdot \nabla \varphi =\varphi \nabla ^2\psi +2\nabla \varphi \cdot \nabla \psi +\psi \nabla ^2\varphi =\varphi \varDelta \psi +2\nabla \varphi \cdot \nabla \psi +\psi \varDelta \varphi ∇⋅∇(φψ)=∇⋅(φ∇ψ+ψ∇φ)=φ∇⋅∇ψ+∇φ⋅∇ψ+ψ∇⋅∇φ+∇ψ⋅∇φ=φ∇2ψ+2∇φ⋅∇ψ+ψ∇2φ=φΔψ+2∇φ⋅∇ψ+ψΔφ
式中,算子 Δ = ∇ ⋅ ∇ = ∇ 2 \varDelta =\nabla \cdot \nabla =\nabla ^2 Δ=∇⋅∇=∇2,作用在标量函数上的算子 Δ \varDelta Δ 称为标量拉普拉斯算子,简称拉普拉斯算子或调和算子。在直角坐标系中,它可表示为:
Δ = ∇ ⋅ ∇ = ∇ 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 \varDelta =\nabla \cdot \nabla =\nabla ^2=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2} Δ=∇⋅∇=∇2=∂x2∂2+∂y2∂2+∂z2∂2
1.3.3 高斯定理与格林公式
定理: 设向量 a ⃗ \vec{a} a在一封闭曲面 S S S的内部有连续一阶偏导数,则 a ⃗ \vec{a} a在 S S S上的通量等于该向量的散度对 S S S所围成体积 V V V上的积分,即:
∯ S a ⃗ ⋅ d S ⃗ = ∯ S a ⃗ ⋅ n ⃗ d S = ∭ V d i v a ⃗ d V = ∭ V ∇ ⋅ a ⃗ d V \oiint_S{\vec{a}\cdot}\mathrm{d}\vec{S}=\oiint_S{\vec{a}\cdot \vec{n}}\mathrm{d}S=\iiint_V{\mathrm{div}\vec{a}}dV=\iiint_V{\nabla \cdot \vec{a}}dV ∬Sa⋅dS=∬Sa⋅ndS=∭VdivadV=∭V∇⋅adV
式中, n ⃗ \vec{n} n为 S S S上单位外法线向量; ∇ \nabla ∇ 为哈密顿算子。上式称为高斯-奥斯特罗格拉茨基定理,简称高斯定理,也称为散度形式的高斯公式或散度定理,它建立了
空间区域V上连续函数的三重积分与其边界面S上的曲面积分之间的关系。
证明:(待补充)
- 高斯公式在理论研究和实际工作中有着广泛的应用,是一种有力的数学工具,许多公式都是从高斯公式出发而得到的。
设:
a
⃗
=
P
(
x
,
y
,
z
)
i
⃗
+
Q
(
x
,
y
,
z
)
j
⃗
+
R
(
x
,
y
,
z
)
k
⃗
n
⃗
=
cos
(
n
,
x
)
i
⃗
+
cos
(
n
,
y
)
j
⃗
+
cos
(
n
,
z
)
k
⃗
=
cos
α
i
⃗
+
cos
β
j
⃗
+
cos
γ
k
⃗
\vec{a}=P\left( x,y,z \right) \vec{i}+Q\left( x,y,z \right) \vec{j}+R\left( x,y,z \right) \vec{k} \\ \vec{n}=\cos \left( n,x \right) \vec{i}+\cos \left( n,y \right) \vec{j}+\cos \left( n,z \right) \vec{k}=\cos \alpha \vec{i}+\cos \beta \vec{j}+\cos \gamma \vec{k}
a=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)kn=cos(n,x)i+cos(n,y)j+cos(n,z)k=cosαi+cosβj+cosγk
将以上两式带入高斯公式,可得:
∯ S a ⃗ ⋅ d S ⃗ = ∯ S a ⃗ ⋅ n ⃗ d S = ∯ S ( P cos α + Q cos β + R cos γ ) d S = ∭ V ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d V \oiint_S{\vec{a}\cdot}\mathrm{d}\vec{S}=\oiint_S{\vec{a}\cdot \vec{n}}\mathrm{d}S=\oiint_S{\left( P\cos \alpha +Q\cos \beta +R\cos \gamma \right)}\mathrm{d}S=\iiint_V{\left( \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \right)}dV ∬Sa⋅dS=∬Sa⋅ndS=∬S(Pcosα+Qcosβ+Rcosγ)dS=∭V(∂x∂P+∂y∂Q+∂z∂R)dV
这个高斯公式是常见的一种形式。

设有平面向量场
a
⃗
\vec{a}
a,在场内取一有向曲线
Γ
\varGamma
Γ ,
d
Γ
\mathrm{d}\varGamma
dΓ 是
Γ
\varGamma
Γ上的曲线元素,在
d
Γ
\mathrm{d}\varGamma
dΓ任取一点
M
M
M,
n
⃗
\vec{n}
n是点
M
M
M处外法线方向的单位向量,若将
a
⃗
⋅
n
⃗
d
Γ
\vec{a}\cdot \vec{n}\mathrm{d}\varGamma
a⋅ndΓ对于曲线
d
Γ
\mathrm{d}\varGamma
dΓ积分:
Φ
=
∫
Γ
a
⃗
⋅
n
⃗
d
Γ
=
∫
Γ
a
⃗
d
Γ
⃗
\varPhi =\int_{\varGamma}{\vec{a}\cdot \vec{n}\mathrm{d}\varGamma}=\int_{\varGamma}{\vec{a}\mathrm{d}\vec{\varGamma}}
Φ=∫Γa⋅ndΓ=∫ΓadΓ
则称为
Φ
\varPhi
Φ 向量场
a
⃗
\vec{a}
a沿法向向量
n
⃗
\vec{n}
n的方向通过曲线
Γ
\varGamma
Γ的通量。在直角坐标系中,曲线
Γ
\varGamma
Γ的法向单位向量
n
⃗
\vec{n}
n、切向单位向量
τ
⃗
\vec{\tau}
τ与该曲线存在下列关系:
{
n
⃗
=
n
⃗
x
+
n
⃗
y
=
n
x
i
⃗
+
n
y
j
⃗
=
cos
(
n
⃗
,
x
)
i
⃗
+
cos
(
n
⃗
,
y
)
j
⃗
=
cos
(
τ
⃗
,
y
)
i
⃗
+
cos
(
τ
⃗
,
−
x
)
j
⃗
=
d
y
d
Γ
i
⃗
−
d
x
d
Γ
j
⃗
τ
⃗
=
τ
⃗
x
+
τ
⃗
y
=
τ
x
i
⃗
+
τ
y
j
⃗
=
cos
(
τ
⃗
,
x
)
i
⃗
+
cos
(
τ
⃗
,
y
)
j
⃗
=
cos
(
n
⃗
,
−
y
)
i
⃗
+
cos
(
n
⃗
,
x
)
j
⃗
=
−
d
x
d
Γ
i
⃗
+
d
y
d
Γ
j
⃗
\begin{cases} \vec{n}=\vec{n}_x+\vec{n}_{\mathrm{y}}=n_x\vec{i}+n_{\mathrm{y}}\vec{j}=\cos \left( \vec{n},x \right) \vec{i}+\cos \left( \vec{n},y \right) \vec{j}=\cos \left( \vec{\tau},y \right) \vec{i}+\cos \left( \vec{\tau},-x \right) \vec{j}=\frac{\mathrm{d}y}{\mathrm{d}\varGamma}\vec{i}-\frac{\mathrm{d}x}{\mathrm{d}\varGamma}\vec{j}\\ \vec{\tau}=\vec{\tau}_x+\vec{\tau}_{\mathrm{y}}=\tau _x\vec{i}+\tau _{\mathrm{y}}\vec{j}=\cos \left( \vec{\tau},x \right) \vec{i}+\cos \left( \vec{\tau},y \right) \vec{j}=\cos \left( \vec{n},-y \right) \vec{i}+\cos \left( \vec{n},x \right) \vec{j}=-\frac{\mathrm{d}x}{\mathrm{d}\varGamma}\vec{i}+\frac{\mathrm{d}y}{\mathrm{d}\varGamma}\vec{j}\\ \end{cases}
{n=nx+ny=nxi+nyj=cos(n,x)i+cos(n,y)j=cos(τ,y)i+cos(τ,−x)j=dΓdyi−dΓdxjτ=τx+τy=τxi+τyj=cos(τ,x)i+cos(τ,y)j=cos(n,−y)i+cos(n,x)j=−dΓdxi+dΓdyj
设
a
⃗
=
P
(
x
,
y
)
i
⃗
+
Q
(
x
,
y
)
j
⃗
\vec{a}=P\left( x,y \right) \vec{i}+Q\left( x,y \right) \vec{j}
a=P(x,y)i+Q(x,y)j,则通过曲线
Γ
\varGamma
Γ的通量
Φ
\varPhi
Φ可写成:
Φ
=
∫
Γ
a
⃗
⋅
n
⃗
d
Γ
=
∫
Γ
a
⃗
d
Γ
⃗
=
∫
Γ
(
P
d
y
−
Q
d
x
)
\varPhi =\int_{\varGamma}{\vec{a}\cdot \vec{n}}\mathrm{d}\varGamma =\int_{\varGamma}{\vec{a}}\mathrm{d}\vec{\varGamma}=\int_{\varGamma}{\left( P\mathrm{d}y-Q\mathrm{d}x \right)}
Φ=∫Γa⋅ndΓ=∫ΓadΓ=∫Γ(Pdy−Qdx)
设有平面向量场 a ⃗ = a ⃗ ( M ) \vec{a}=\vec{a}\left( M \right) a=a(M) ,在场中一点 M M M的某个邻域内作包含此点的任一封闭曲线 Δ Γ \varDelta \varGamma ΔΓ , Δ Γ \varDelta \varGamma ΔΓ所围成的面积为 Δ D \varDelta D ΔD,计算向量 a ⃗ \vec{a} a经过 Δ Γ \varDelta \varGamma ΔΓ线上的通量,当 Δ D \varDelta D ΔD以任意方式向点 M M M收缩时,如果比式:
lim Δ D → 0 Δ Φ Δ D = lim Δ D → 0 ∮ Δ Γ a ⃗ ⋅ n ⃗ d Γ Δ D \underset{\varDelta D\rightarrow 0}{\lim}\frac{\varDelta \varPhi}{\varDelta D}=\underset{\varDelta D\rightarrow 0}{\lim}\frac{\oint_{\varDelta \varGamma}{\vec{a}\cdot \vec{n}}\mathrm{d}\varGamma}{\varDelta D} ΔD→0limΔDΔΦ=ΔD→0limΔD∮ΔΓa⋅ndΓ
的极限存在,则此极限称为向量函数 a ⃗ \vec{a} a在点 M M M的散度,记作 d i v a ⃗ \mathrm{div}\vec{a} diva,当采用哈密顿算子时,可写作 ∇ ⋅ a ⃗ \nabla \cdot \vec{a} ∇⋅a,即:
d i v a ⃗ = ∇ ⋅ a ⃗ = lim Δ D → 0 Δ Φ Δ D = lim Δ D → 0 ∮ Δ Γ a ⃗ ⋅ n ⃗ d Γ Δ D \mathrm{div}\vec{a}=\nabla \cdot \vec{a}=\underset{\varDelta D\rightarrow 0}{\lim}\frac{\varDelta \varPhi}{\varDelta D}=\underset{\varDelta D\rightarrow 0}{\lim}\frac{\oint_{\varDelta \varGamma}{\vec{a}\cdot \vec{n}}\mathrm{d}\varGamma}{\varDelta D} diva=∇⋅a=ΔD→0limΔDΔΦ=ΔD→0limΔD∮ΔΓa⋅ndΓ
显然点
M
M
M的散度与所取的封闭曲线
Δ
Γ
\varDelta \varGamma
ΔΓ的形状无关,它是一个不依赖于坐标系选取的数量,因此是一个标量。
令
b
⃗
=
ϕ
a
⃗
\vec{b}=\phi \vec{a}
b=ϕa,利用散度的性质,可得到以下公式:
∭
V
d
i
v
(
ϕ
a
⃗
)
d
V
=
∭
V
∇
⋅
(
ϕ
a
⃗
)
d
V
=
∭
V
(
ϕ
∇
⋅
a
⃗
+
a
⃗
∇
ϕ
)
d
V
=
∯
S
ϕ
a
⃗
⋅
d
S
⃗
=
∯
S
ϕ
(
a
⃗
⋅
n
⃗
)
d
S
\iiint_V{\mathrm{div}\left( \phi \vec{a} \right)}\mathrm{d}V=\iiint_V{\nabla \cdot \left( \phi \vec{a} \right)}\mathrm{d}V=\iiint_V{\left( \phi \nabla \cdot \vec{a}+\vec{a}\nabla \phi \right)}\mathrm{d}V \\ =\oiint_S{\phi \vec{a}}\cdot \mathrm{d}\vec{S}=\oiint_S{\phi \left( \vec{a}\cdot \vec{n} \right)}\mathrm{d}S
∭Vdiv(ϕa)dV=∭V∇⋅(ϕa)dV=∭V(ϕ∇⋅a+a∇ϕ)dV=∬Sϕa⋅dS=∬Sϕ(a⋅n)dS
定理: 设平面向量 a ⃗ \vec{a} a在一封闭曲线 Γ \varGamma Γ 的内部有连续一阶偏导数,则 a ⃗ \vec{a} a在 Γ \varGamma Γ上的通量等于该向量的散度对 Γ \varGamma Γ所围成面积 D D D上的积分,即:
∮ Γ a ⃗ ⋅ n ⃗ d Γ = ∮ Γ a n d Γ = ∬ D d i v a ⃗ d D = ∬ D ∇ ⋅ a ⃗ d D \oint_{\varGamma}{\vec{a}\cdot \vec{n}}\mathrm{d}\varGamma =\oint_{\varGamma}{a_n}\mathrm{d}\varGamma =\iint_D{\mathrm{div}\vec{a}}\mathrm{d}D=\iint_D{\nabla \cdot \vec{a}}\mathrm{d}D ∮Γa⋅ndΓ=∮ΓandΓ=∬DdivadD=∬D∇⋅adD
式中, n ⃗ \vec{n} n为 Γ \varGamma Γ上外法线方向的单位向量; ∇ \nabla ∇为哈密顿算子。上式称为格林公式或格林定理,它建立了平面区域 D D D上的二重积分和沿该区域边界 Γ \varGamma Γ的曲线积分之间的联系。
- 证明的方法与高斯定理的证明方法相同,只需将封闭曲面 S S S换成封闭曲线 Γ \varGamma Γ,并将 S S S围成的体积 V V V换成 Γ \varGamma Γ围成的面积 D D D即可。
设
a
⃗
=
Q
(
x
,
y
)
i
⃗
−
P
(
x
,
y
)
j
⃗
\vec{a}=Q\left( x,y \right) \vec{i}-P\left( x,y \right) \vec{j}
a=Q(x,y)i−P(x,y)j,并注意到
n
⃗
=
d
y
d
Γ
i
⃗
−
d
x
d
Γ
j
⃗
\vec{n}=\frac{\mathrm{d}y}{\mathrm{d}\varGamma}\vec{i}-\frac{\mathrm{d}x}{\mathrm{d}\varGamma}\vec{j}
n=dΓdyi−dΓdxj,则格林公式可写成:
∮
Γ
(
P
(
x
,
y
)
d
x
+
Q
(
x
,
y
)
d
y
)
=
∬
D
(
∂
Q
∂
x
−
∂
P
∂
y
)
d
x
d
y
\oint_{\varGamma}{\left( P\left( x,y \right) \mathrm{d}x+Q\left( x,y \right) \mathrm{d}y \right)}=\iint_D{\left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right)}\mathrm{d}x\mathrm{d}y
∮Γ(P(x,y)dx+Q(x,y)dy)=∬D(∂x∂Q−∂y∂P)dxdy
这里曲线积分沿着曲线 Γ \varGamma Γ的正向,二重积分展布在区域 D D D上。所谓曲线 Γ \varGamma Γ的正向是这样的方向,设想一个人绕着曲线 Γ \varGamma Γ行走,使得 Γ \varGamma Γ围成的区域 D D D总是保持在其左侧。
令
P
=
−
y
,
Q
=
x
P=-y,Q=x
P=−y,Q=x,则有:
D
=
∬
D
d
x
d
y
=
1
2
∮
Γ
(
x
d
y
−
y
d
x
)
D=\iint_D{\mathrm{d}x\mathrm{d}y}=\frac{1}{2}\oint_{\varGamma}{\left( x\mathrm{d}y-y\mathrm{d}x \right)}
D=∬Ddxdy=21∮Γ(xdy−ydx)
上式为利用曲线积分计算平面区域
D
D
D的面积公式
若 x = x ( t ) , y = y ( t ) x=x\left( t \right) ,y=y\left( t \right) x=x(t),y=y(t),则上式可写成: D = ∬ D d x d y = 1 2 ∮ Γ ( x y ˙ − y x ˙ ) d t D=\iint_D{\mathrm{d}x\mathrm{d}y}=\frac{1}{2}\oint_{\varGamma}{\left( x\dot{y}-y\dot{x} \right)}\mathrm{d}t D=∬Ddxdy=21∮Γ(xy˙−yx˙)dt
令
P
=
u
∂
u
∂
y
,
Q
=
−
u
∂
u
∂
x
P=u\frac{\partial u}{\partial y},Q=-u\frac{\partial u}{\partial x}
P=u∂y∂u,Q=−u∂x∂u,则有:
∬
D
(
∂
2
u
∂
x
2
+
∂
2
u
∂
y
2
)
u
d
x
d
y
+
∬
D
[
(
∂
u
∂
x
)
2
+
(
∂
u
∂
y
)
2
]
d
x
d
y
=
−
∮
Γ
(
u
∂
u
∂
y
d
x
−
u
∂
u
∂
x
d
y
)
\iint_D{\left( \frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2} \right) u\mathrm{d}x\mathrm{d}y}+\iint_D{\left[ \left( \frac{\partial u}{\partial x} \right) ^2+\left( \frac{\partial u}{\partial y} \right) ^2 \right] \mathrm{d}x\mathrm{d}y}=-\oint_{\varGamma}{\left( u\frac{\partial u}{\partial y}\mathrm{d}x-u\frac{\partial u}{\partial x}\mathrm{d}y \right)}
∬D(∂x2∂2u+∂y2∂2u)udxdy+∬D[(∂x∂u)2+(∂y∂u)2]dxdy=−∮Γ(u∂y∂udx−u∂x∂udy)
设函数
φ
、
ψ
\varphi \text{、}\psi
φ、ψ 和
λ
\lambda
λ 在区域
V
V
V内有连续二阶导数,令
a
⃗
=
φ
λ
∇
ψ
\vec{a}=\varphi \lambda \nabla \psi
a=φλ∇ψ ,根据散度的性质,有下面公式:
∇
⋅
a
⃗
=
∇
⋅
(
φ
λ
∇
ψ
)
=
φ
∇
⋅
(
λ
∇
ψ
)
+
λ
∇
φ
⋅
∇
ψ
\nabla \cdot \vec{a}=\nabla \cdot \left( \varphi \lambda \nabla \psi \right) =\varphi \nabla \cdot \left( \lambda \nabla \psi \right) +\lambda \nabla \varphi \cdot \nabla \psi
∇⋅a=∇⋅(φλ∇ψ)=φ∇⋅(λ∇ψ)+λ∇φ⋅∇ψ
进而可知:
a
⃗
⋅
n
⃗
=
φ
λ
∇
ψ
⋅
n
⃗
=
φ
λ
∣
∇
ψ
∣
n
⃗
⋅
n
⃗
=
φ
λ
∂
ψ
∂
n
\vec{a}\cdot \vec{n}=\varphi \lambda \nabla \psi \cdot \vec{n}=\varphi \lambda \left| \nabla \psi \right|\vec{n}\cdot \vec{n}=\varphi \lambda \frac{\partial \psi}{\partial n}
a⋅n=φλ∇ψ⋅n=φλ∣∇ψ∣n⋅n=φλ∂n∂ψ
∭
V
∇
⋅
(
φ
λ
∇
ψ
)
d
V
=
∭
V
[
φ
∇
⋅
(
λ
∇
ψ
)
+
λ
∇
φ
⋅
∇
ψ
]
d
V
=
∯
S
φ
λ
∂
ψ
∂
n
d
S
=
∯
S
φ
λ
∣
∇
ψ
∣
d
S
=
∯
S
φ
λ
∇
ψ
⋅
n
⃗
d
S
\iiint_V{\nabla \cdot \left( \varphi \lambda \nabla \psi \right)}\mathrm{d}V=\iiint_V{\left[ \varphi \nabla \cdot \left( \lambda \nabla \psi \right) +\lambda \nabla \varphi \cdot \nabla \psi \right]}\mathrm{d}V \\ =\oiint_S{\varphi \lambda \frac{\partial \psi}{\partial n}}\mathrm{d}S=\oiint_S{\varphi \lambda \left| \nabla \psi \right|}\mathrm{d}S=\oiint_S{\varphi \lambda \nabla \psi \cdot \vec{n}}\mathrm{d}S
∭V∇⋅(φλ∇ψ)dV=∭V[φ∇⋅(λ∇ψ)+λ∇φ⋅∇ψ]dV=∬Sφλ∂n∂ψdS=∬Sφλ∣∇ψ∣dS=∬Sφλ∇ψ⋅ndS
若令上式中的
λ
=
1
\lambda =1
λ=1,则可得到格林第一公式或奥斯特罗格拉茨基公式,也称为
格林第一定理或奥氏公式,即:
∭
V
∇
⋅
(
φ
∇
ψ
)
d
V
=
∭
V
(
φ
∇
⋅
∇
ψ
+
∇
φ
⋅
∇
ψ
)
d
V
=
∭
V
(
φ
Δ
ψ
+
∇
φ
⋅
∇
ψ
)
d
V
=
∯
S
φ
∂
ψ
∂
n
d
S
=
∯
S
φ
λ
∣
∇
ψ
∣
d
S
=
∯
S
φ
n
⃗
⋅
∇
ψ
d
S
\iiint_V{\nabla \cdot \left( \varphi \nabla \psi \right)}\mathrm{d}V=\iiint_V{\left( \varphi \nabla \cdot \nabla \psi +\nabla \varphi \cdot \nabla \psi \right)}\mathrm{d}V=\iiint_V{\left( \varphi \varDelta \psi +\nabla \varphi \cdot \nabla \psi \right)}\mathrm{d}V \\ =\oiint_S{\varphi \frac{\partial \psi}{\partial n}}\mathrm{d}S=\oiint_S{\varphi \lambda \left| \nabla \psi \right|}\mathrm{d}S=\oiint_S{\varphi \vec{n}\cdot \nabla \psi}\mathrm{d}S
∭V∇⋅(φ∇ψ)dV=∭V(φ∇⋅∇ψ+∇φ⋅∇ψ)dV=∭V(φΔψ+∇φ⋅∇ψ)dV=∬Sφ∂n∂ψdS=∬Sφλ∣∇ψ∣dS=∬Sφn⋅∇ψdS
将上式中的
φ
\varphi
φ与
ψ
\psi
ψ易位,得:
∭
V
∇
⋅
(
ψ
∇
φ
)
d
V
=
∭
V
(
ψ
Δ
φ
+
∇
ψ
⋅
∇
φ
)
d
V
=
∯
S
ψ
∂
φ
∂
n
d
S
=
∯
S
ψ
∣
∇
φ
∣
d
S
=
∯
S
ψ
∇
φ
⋅
n
⃗
d
S
\iiint_V{\nabla \cdot \left( \psi \nabla \varphi \right)}\mathrm{d}V=\iiint_V{\left( \psi \varDelta \varphi +\nabla \psi \cdot \nabla \varphi \right)}\mathrm{d}V=\oiint_S{\psi \frac{\partial \varphi \,\,}{\partial n}}\mathrm{d}S \\ =\oiint_S{\psi \left| \nabla \varphi \right|}\mathrm{d}S=\oiint_S{\psi \nabla \varphi \cdot}\vec{n}\mathrm{d}S
∭V∇⋅(ψ∇φ)dV=∭V(ψΔφ+∇ψ⋅∇φ)dV=∬Sψ∂n∂φdS=∬Sψ∣∇φ∣dS=∬Sψ∇φ⋅ndS
也是格林第一公式的另一种形式。将格林第一公式两种不同形式相减,便得到格林第二公式,也称为格林第二定理,即:
∭
V
(
φ
Δ
ψ
−
ψ
Δ
φ
)
d
V
=
∯
S
(
φ
∂
ψ
∂
n
−
ψ
∂
φ
∂
n
)
d
S
=
∯
S
(
φ
∇
ψ
−
ψ
∇
φ
)
⋅
n
⃗
d
S
\iiint_V{\left( \varphi \varDelta \psi -\psi \varDelta \varphi \right)}\mathrm{d}V=\oiint_S{\left( \varphi \frac{\partial \psi}{\partial n}-\psi \frac{\partial \varphi \,\,}{\partial n} \right)}\mathrm{d}S=\oiint_S{\left( \varphi \nabla \psi -\psi \nabla \varphi \right) \cdot \vec{n}}\mathrm{d}S
∭V(φΔψ−ψΔφ)dV=∬S(φ∂n∂ψ−ψ∂n∂φ)dS=∬S(φ∇ψ−ψ∇φ)⋅ndS
当
φ
=
ψ
\varphi =\psi
φ=ψ时,即可得到格林第三公式,也称为格林第三定理,即:
∭
V
[
φ
Δ
φ
+
(
∇
φ
)
2
]
d
V
=
∯
S
φ
∂
ψ
∂
n
d
S
=
∯
S
φ
∇
φ
⋅
n
⃗
d
S
\iiint_V{\left[ \varphi \varDelta \varphi +\left( \nabla \varphi \right) ^2 \right]}\mathrm{d}V=\oiint_S{\varphi \frac{\partial \psi \,\,}{\partial n}}\mathrm{d}S=\oiint_S{\varphi \nabla \varphi}\cdot \vec{n}\mathrm{d}S
∭V[φΔφ+(∇φ)2]dV=∬Sφ∂n∂ψdS=∬Sφ∇φ⋅ndS
令
ψ
=
1
\psi =1
ψ=1,则:
∭
V
Δ
φ
d
V
=
∯
S
φ
∂
φ
∂
n
d
S
=
∯
S
φ
∇
φ
⋅
n
⃗
d
S
\iiint_V{\varDelta \varphi}\mathrm{d}V=\oiint_S{\varphi \frac{\partial \varphi \,\,}{\partial n}}\mathrm{d}S=\oiint_S{\varphi \nabla \varphi \cdot \vec{n}}\mathrm{d}S
∭VΔφdV=∬Sφ∂n∂φdS=∬Sφ∇φ⋅ndS
在直角坐标系中,上式可写成:
∭
V
(
∂
2
φ
∂
x
2
+
∂
2
φ
∂
y
2
+
∂
2
φ
∂
z
2
)
d
V
=
∯
S
(
∂
φ
∂
x
d
y
d
z
+
∂
φ
∂
y
d
z
d
x
+
∂
φ
∂
z
d
x
d
y
)
\iiint_V{\left( \frac{\partial ^2\varphi \,\,}{\partial x^2}+\frac{\partial ^2\varphi \,\,}{\partial y^2}+\frac{\partial ^2\varphi \,\,}{\partial z^2} \right)}\mathrm{d}V=\oiint_S{\left( \frac{\partial \varphi \,\,}{\partial x}\mathrm{d}y\mathrm{d}z+\frac{\partial \varphi \,\,}{\partial y}\mathrm{d}z\mathrm{d}x+\frac{\partial \varphi \,\,}{\partial z}\mathrm{d}x\mathrm{d}y \right)}
∭V(∂x2∂2φ+∂y2∂2φ+∂z2∂2φ)dV=∬S(∂x∂φdydz+∂y∂φdzdx+∂z∂φdxdy)
若
Δ
φ
=
0
\varDelta \varphi =0
Δφ=0,则:
∭
V
(
Δ
φ
)
2
d
V
=
∯
S
φ
∂
φ
∂
n
d
S
=
∯
S
φ
∇
φ
⋅
n
⃗
d
S
∯
S
∂
φ
∂
n
d
S
=
∯
S
∇
φ
⋅
n
⃗
d
S
\iiint_V{\left( \varDelta \varphi \right) ^2}\mathrm{d}V=\oiint_S{\varphi \frac{\partial \varphi \,\,}{\partial n}}\mathrm{d}S=\oiint_S{\varphi \nabla \varphi \cdot \vec{n}}\mathrm{d}S \\ \oiint_S{\frac{\partial \varphi \,\,}{\partial n}}\mathrm{d}S=\oiint_S{\nabla \varphi \cdot \vec{n}}\mathrm{d}S
∭V(Δφ)2dV=∬Sφ∂n∂φdS=∬Sφ∇φ⋅ndS∬S∂n∂φdS=∬S∇φ⋅ndS
同理,只需将对封闭曲面
S
S
S的积分换成对封闭曲线
Γ
\varGamma
Γ 的积分,将对
S
S
S围成的体积
V
V
V的积分换成对
Γ
\varGamma
Γ围成的面积
D
D
D的积分,并将三维的哈密顿算子和拉普拉斯算子换成二维的即可。
从历史上看,格林公式是独立提出来的,因而是一个原始公式。但由于它和高斯公式密切相关,故可认为高斯公式是平面格林公式在空间的推广,而格林公式是高斯公式在平面上的特殊情况。
- 若将格林第一公式中的
φ
\varphi
φ换成
Δ
φ
\varDelta \varphi
Δφ,则有:
∭ V ∇ ⋅ ( Δ φ ∇ ψ ) d V = ∭ V ( Δ φ ∇ ⋅ ∇ ψ + ∇ Δ φ ⋅ ∇ ψ ) d V = ∭ V ( Δ φ Δ ψ + ∇ Δ φ ⋅ ∇ ψ ) d V = ∯ S Δ φ ∂ ψ ∂ n d S = ∯ S Δ φ n ⋅ ∇ ψ d S \iiint_V{\nabla \cdot \left( \varDelta \varphi \nabla \psi \right)}\mathrm{d}V=\iiint_V{\left( \varDelta \varphi \nabla \cdot \nabla \psi +\nabla \varDelta \varphi \cdot \nabla \psi \right)}\mathrm{d}V=\iiint_V{\left( \varDelta \varphi \varDelta \psi +\nabla \varDelta \varphi \cdot \nabla \psi \right)}\mathrm{d}V \\ =\oiint_S{\varDelta \varphi \frac{\partial \psi}{\partial n}}\mathrm{d}S=\oiint_S{\varDelta \varphi n\cdot \nabla \psi}\mathrm{d}S ∭V∇⋅(Δφ∇ψ)dV=∭V(Δφ∇⋅∇ψ+∇Δφ⋅∇ψ)dV=∭V(ΔφΔψ+∇Δφ⋅∇ψ)dV=∬SΔφ∂n∂ψdS=∬SΔφn⋅∇ψdS - 若将格林第一公式中的
ψ
\psi
ψ换成
Δ
ψ
\varDelta \psi
Δψ,则有:
∭ V ∇ ⋅ ( φ ∇ Δ ψ ) d V = ∭ V ( φ ∇ ⋅ ∇ Δ ψ + ∇ φ ⋅ ∇ Δ ψ ) d V = ∭ V ( φ Δ 2 ψ + ∇ φ ⋅ ∇ Δ ψ ) d V = ∯ S φ ∂ Δ ψ ∂ n d S = ∯ S φ n ⋅ ∇ Δ ψ d S \iiint_V{\nabla \cdot \left( \varphi \nabla \varDelta \psi \right)}\mathrm{d}V=\iiint_V{\left( \varphi \nabla \cdot \nabla \varDelta \psi +\nabla \varphi \cdot \nabla \varDelta \psi \right)}\mathrm{d}V=\iiint_V{\left( \varphi \varDelta ^2\psi +\nabla \varphi \cdot \nabla \varDelta \psi \right)}\mathrm{d}V \\ =\oiint_S{\varphi \frac{\partial \varDelta \psi}{\partial n}}\mathrm{d}S=\oiint_S{\varphi n\cdot \nabla \varDelta \psi}\mathrm{d}S ∭V∇⋅(φ∇Δψ)dV=∭V(φ∇⋅∇Δψ+∇φ⋅∇Δψ)dV=∭V(φΔ2ψ+∇φ⋅∇Δψ)dV=∬Sφ∂n∂ΔψdS=∬Sφn⋅∇ΔψdS
将上式中的 φ \varphi φ与 ψ \psi ψ易位,得:
∭ V ∇ ⋅ ( ψ ∇ Δ φ ) d V = ∭ V ∇ ( ψ ∇ ⋅ ∇ Δ φ + ∇ ψ ⋅ ∇ Δ φ ) d V = ∭ V ∇ ( ψ Δ 2 φ + ∇ ψ ⋅ ∇ Δ φ ) d V = ∯ S ψ ∂ Δ φ ∂ n d S = ∯ S ψ n ⋅ ∇ Δ φ \iiint_V{\nabla \cdot \left( \psi \nabla \varDelta \varphi \right)}\mathrm{d}V=\iiint_V{\nabla \left( \psi \nabla \cdot \nabla \varDelta \varphi +\nabla \psi \cdot \nabla \varDelta \varphi \right)}\mathrm{d}V=\iiint_V{\nabla \left( \psi \varDelta ^2\varphi +\nabla \psi \cdot \nabla \varDelta \varphi \right)}\mathrm{d}V \\ =\oiint_S{\psi \frac{\partial \varDelta \varphi}{\partial n}}\mathrm{d}S=\oiint_S{\psi n\cdot \nabla \varDelta \varphi} ∭V∇⋅(ψ∇Δφ)dV=∭V∇(ψ∇⋅∇Δφ+∇ψ⋅∇Δφ)dV=∭V∇(ψΔ2φ+∇ψ⋅∇Δφ)dV=∬Sψ∂n∂ΔφdS=∬Sψn⋅∇Δφ
进一步整理则有:
∭ V ψ Δ 2 φ d V = − ∭ V ∇ ψ ⋅ ∇ Δ φ d V + ∯ S ψ ∂ Δ φ ∂ n d S = ∭ V Δ φ Δ ψ d V + ∯ S ( ψ ∂ Δ φ ∂ n − Δ φ ∂ ψ ∂ n ) d S \iiint_V{\psi \varDelta ^2\varphi}\mathrm{d}V=-\iiint_V{\nabla \psi \cdot \nabla \varDelta \varphi}\mathrm{d}V+\oiint_S{\psi \frac{\partial \varDelta \varphi}{\partial n}}\mathrm{d}S \\ =\iiint_V{\varDelta \varphi \varDelta \psi}\mathrm{d}V+\oiint_S{\left( \psi \frac{\partial \varDelta \varphi}{\partial n}-\varDelta \varphi \frac{\partial \psi}{\partial n} \right)}\mathrm{d}S ∭VψΔ2φdV=−∭V∇ψ⋅∇ΔφdV+∬Sψ∂n∂ΔφdS=∭VΔφΔψdV+∬S(ψ∂n∂Δφ−Δφ∂n∂ψ)dS
若标量函数
φ
\varphi
φ在封闭曲面
S
S
S内具有连续的一阶偏导数,且
S
S
S所围成的体积为
V
V
V,则有下列梯度公式:
∯
S
φ
d
S
⃗
=
∯
S
φ
n
⃗
d
S
=
∯
S
n
⃗
φ
d
S
=
∭
V
g
r
a
d
φ
d
V
=
∭
V
∇
φ
d
V
\oiint_S{\varphi}\mathrm{d}\vec{S}=\oiint_S{\varphi \vec{n}}\mathrm{d}S=\oiint_S{\vec{n}\varphi}\mathrm{d}S=\iiint_V{\mathrm{grad}\varphi}\mathrm{d}V=\iiint_V{\nabla \varphi}\mathrm{d}V
∬SφdS=∬SφndS=∬SnφdS=∭VgradφdV=∭V∇φdV
上式称为梯度形式的高斯公式或梯度定理。
证明:(待补充)
例: 设 v Δ ( p Δ u ) = u Δ ( p Δ v ) v\varDelta \left( p\varDelta u \right) =u\varDelta \left( p\varDelta v \right) vΔ(pΔu)=uΔ(pΔv),求证: ∇ ⋅ [ v ∇ ( p Δ u ) − u ∇ ( p Δ v ) + p Δ v ∇ u − p Δ u ∇ v ] = 0 \nabla \cdot \left[ v\nabla \left( p\varDelta u \right) -u\nabla \left( p\varDelta v \right) +p\varDelta v\nabla u-p\varDelta u\nabla v \right] =0 ∇⋅[v∇(pΔu)−u∇(pΔv)+pΔv∇u−pΔu∇v]=0
令: φ = p Δ u , ψ = p Δ v \varphi =p\varDelta u,\psi =p\varDelta v φ=pΔu,ψ=pΔv,根据散度的性质有:
v Δ ( p Δ u ) = v Δ φ = ∇ ⋅ ( v ∇ φ ) − ∇ v ⋅ ∇ φ v\varDelta \left( p\varDelta u \right) =v\varDelta \varphi =\nabla \cdot \left( v\nabla \varphi \right) -\nabla v\cdot \nabla \varphi vΔ(pΔu)=vΔφ=∇⋅(v∇φ)−∇v⋅∇φ
其中: ∇ v ⋅ ∇ φ = ∇ ⋅ ( φ ∇ v ) − φ ∇ ⋅ ∇ v = ∇ ⋅ ( φ ∇ v ) − φ Δ v \nabla v\cdot \nabla \varphi =\nabla \cdot \left( \varphi \nabla v \right) -\varphi \nabla \cdot \nabla v=\nabla \cdot \left( \varphi \nabla v \right) -\varphi \varDelta v ∇v⋅∇φ=∇⋅(φ∇v)−φ∇⋅∇v=∇⋅(φ∇v)−φΔv,带入上式可得: v Δ ( p Δ u ) = v Δ φ = ∇ ⋅ ( v ∇ φ − φ ∇ v ) + φ Δ v v\varDelta \left( p\varDelta u \right) =v\varDelta \varphi =\nabla \cdot \left( v\nabla \varphi -\varphi \nabla v \right) +\varphi \varDelta v vΔ(pΔu)=vΔφ=∇⋅(v∇φ−φ∇v)+φΔv
将 u , v u,v u,v易位,并由 ψ = p Δ v \psi =p\varDelta v ψ=pΔv可得: u Δ ( p Δ v ) = u Δ ψ = ∇ ⋅ ( u ∇ ψ − ψ ∇ u ) + ψ Δ u u\varDelta \left( p\varDelta v \right) =u\varDelta \psi =\nabla \cdot \left( u\nabla \psi -\psi \nabla u \right) +\psi \varDelta u uΔ(pΔv)=uΔψ=∇⋅(u∇ψ−ψ∇u)+ψΔu
将上述两式相减,并注意到有: φ ∇ v = ψ Δ u = p Δ v Δ u \varphi \nabla v=\psi \varDelta u=p\varDelta v\varDelta u φ∇v=ψΔu=pΔvΔu,得:
∇ ⋅ ( v ∇ φ − u ∇ ψ + ψ ∇ u − φ ∇ v ) = 0 ∇ ⋅ [ v ∇ ( p Δ u ) − u ∇ ( p Δ v ) + p Δ v ∇ u − p Δ u ∇ v ] = 0 \nabla \cdot \left( v\nabla \varphi -u\nabla \psi +\psi \nabla u-\varphi \nabla v \right) =0 \\ \nabla \cdot \left[ v\nabla \left( p\varDelta u \right) -u\nabla \left( p\varDelta v \right) +p\varDelta v\nabla u-p\varDelta u\nabla v \right] =0 ∇⋅(v∇φ−u∇ψ+ψ∇u−φ∇v)=0∇⋅[v∇(pΔu)−u∇(pΔv)+pΔv∇u−pΔu∇v]=0