210. 课程表 II

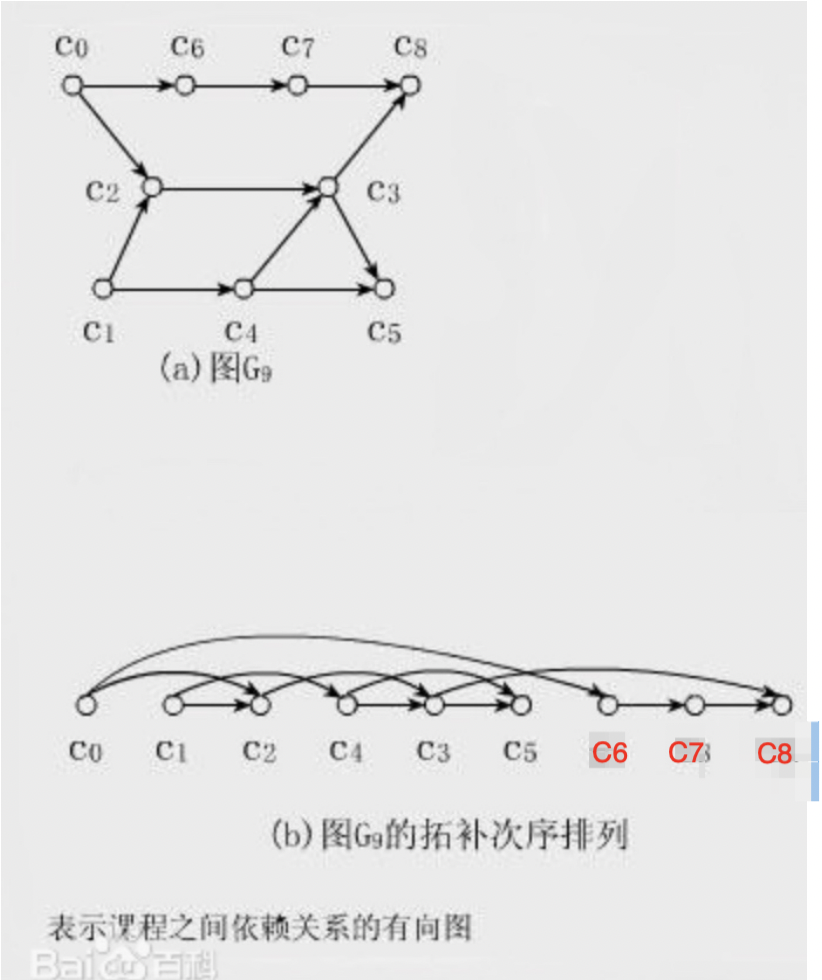
该题用到「拓扑排序」的算法思想，关于拓扑排序，直观地说就是，让你把⼀幅图「拉平」，⽽且这个「拉平」的图⾥⾯，所有箭头⽅向都是⼀致的，⽐如上图所有箭头都是朝右的。
很显然，如果⼀幅有向图中存在环，是⽆法进⾏拓扑排序的，因为肯定做不到所有箭头⽅向⼀致；反过来，如果⼀幅图是「有向⽆环图」，那么⼀定可以进⾏拓扑排序。

class TopologicalSorting:
    """
    拓扑排序算法
    课程表II，给出可能的课程安排顺序
    https://leetcode.cn/problems/course-schedule-ii/
    """
    def __init__(self):
        self.hascycle = False
        self.postorder = []

    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        """
        dfs
        :param numCourses:
        :param prerequisites:
        :return:
        """
        graph = self.buildGraph(numCourses, prerequisites)
        self.visited = [False] * numCourses
        self.onPath = [False] * numCourses

        for i in range(numCourses):
            self.dfs(graph, i)

        if self.hascycle:
            return []

        # 对后序遍历进行反转
        res = self.postorder[::-1]

        return res

    def dfs(self, graph, i):
        if self.onPath[i]:
            self.hascycle = True
            return

        if self.visited[i]:
            return
        # 前序遍历位置
        self.onPath[i] = True
        self.visited[i] = True

        for t in graph[i]:
            self.dfs(graph, t)

        # 后序遍历位置
        self.postorder.append(i)
        self.onPath[i] = False

    def buildGraph(self, numCourses: int, prerequisites: List[List[int]]) -> List[List[int]]:

        # 注意这两种新建对象的区别，前者是传的引用，后者是拷贝一个新的变量
        # graph = [[]] * numCourses
        graph = [[] for _ in range(numCourses)]

        for edge in prerequisites:
            src = edge[1]
            dst = edge[0]
            graph[src].append(dst)

        return graph

    def findOrder2(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        """
        BFS 实现
        借助 indegree 数组实现visited数组的作用，只有入度为0的节点才能入队，不会出现死循环
        :param numCourses:
        :param prerequisites:
        :return:
        """
        graph = self.buildGraph(numCourses, prerequisites)
        self.indegree = [0] * numCourses
        for edge in prerequisites:
            dst = edge[0]
            self.indegree[dst] += 1

        queue = []
        for i in range(numCourses):
            if self.indegree[i] == 0:
                queue.append(i)

        res = [0] * numCourses
        # 记录遍历节点的顺序
        count = 0
        while queue:
            cur = queue.pop(0)
            # 弹出节点的顺序即为拓扑排序结果
            res[count] = cur
            count += 1
            for neighbor in graph[cur]:
                self.indegree[neighbor] -= 1
                if self.indegree[neighbor] == 0:
                    queue.append(neighbor)

        # 存在环
        if count != numCourses:
            return []

        return res