一、面试中数组相关理论知识

数组是非常基础的数据结构，在面试中，考察数组的题目一般在思维上都不难，主要是考察对代码的掌控能力。也就是说，想法很简单，但实现起来 可能就不是那么回事了。

要想真正理解数组在内存中的存储方式，就必须知道数组在内存中的存储方式。

重点就是数组在内存中的存储。

1. 数组是存储在连续内存空间上的相同类型数据的集合。

2. 数组的下标都是从0开始的

3. 数组的内存空间的地址是连续的

4. C++中二维数组在内存中也是连续的，java中没有指针，不对程序猿暴露元素的地址，寻址操作完全交给虚拟机，（即使打印也是经过哈希得到的虚拟地址）所以二维数组的每个元素【一维数组】内部可能是连续的，但是二维数组的元素之间可能不是连续的。

5. 数组元素在内存空间中的地址是连续的，这就意味着我们在进行删除和添加元素的时候需要移动其他元素的地址。

6. 数组的元素是不能删除的，只能进行覆盖

7. 建议：能不能用库函数取决于用库函数是解决这个题目中的一小步，知不知道源码和源码实现以及时间复杂度，如果都是yes，那么可以使用，否则就是建议不用

二、二分查找问题

题目链接

思路

最基本的二分查找

注意事项

1. 在while循环中，如果不是target值，除了修改left或者right值之外，还要修改mid的值。
2. 对于mid的求法，需要用到一个数学技巧。不要直接right和left直接相加，而是用左端值+两者差值的一半。这样做的目的是为了防止right和left的和超出int所能表示的最大范围，导致溢出。

AC代码

class Solution {
    public int search(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        int mid=left+(right-left)/2;
        while(left<=right){
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]<target){
                left=mid+1;
            }else{
                right=mid-1;
            }
            mid=left+(right-left)/2;
        }
        return -1;
    }
}

三、移除元素

题目链接

思路

优化后的核心思路：双指针

因为此题要求空间复杂度为O(1)，也就是说我们不能通过开辟临时数组来解题。那么很显然，这道题需要我们遍历数组，并进行原地修改数组，并且返回“新数组的长度”。

那么，我们应该怎样删除数组元素呢？

时间复杂度为O（n^2）

首先，移除也就是从把元素从数组中删除。但是我们知道数组其实不能从根本上删除元素，而是通过覆盖元素、同时**控制访问地址权限(即“修改数组长度”)**的方式来实现“删除元素的效果的”。

因此，我们可以通过设置cnt变量，初始值为0，来记录当前数组中需要删除的个数，并且在数组遍历的时候减去cnt个数。之后一满足条件就往前覆盖。

我们很容易写出这样的代码，但是它真的能ac吗？have a try.

public int removeElement(int[] nums, int val) {
    int cnt=0;
    for (int i = 0; i < nums.length-cnt; i++) {
        if(nums[i]==val){
            for (int j = i; j <nums.length-1; j++) {
                nums[j]=nums[j+1];
            }
            cnt++;
        }
    }
    return nums.length-cnt;
}

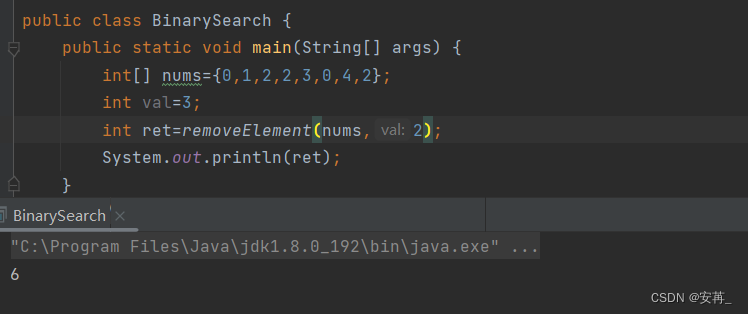
这是什么原因呢？我们调试看看是为什么

调试到这里我们可以发现，第一个2被删除了，但是紧挨的2并没有删除，此时就已经开始遍历下一个位置了。

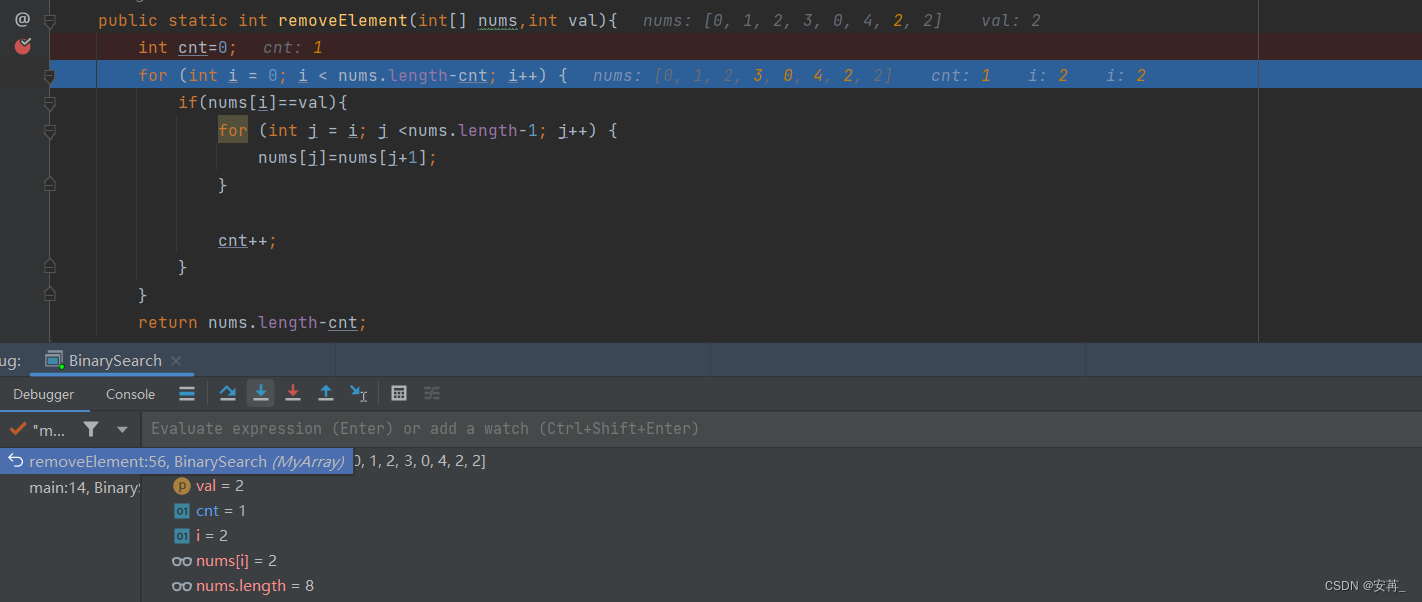
很容易分析出来，是因为我们把后边的值往前拿了，但是后边的值到底是不是target值呢？我们不得而知。

倘若此时我们对代码不加修改，那么它就直接跳到下一个位置去了。相当于图示这种情况。

因此，为了防止这种情况，我们在每次覆盖完成之后需要再次访问这个位置的元素，通过i–实现，看是不是target值。

这样写出的代码时间复杂度是O(n^2)、空间复杂度是O(1)

那么有没有办法将时间复杂度优化成O(n)呢？答案是肯定的

用双指针代替了一层for循环需要做的事情

慢指针是“新数组中的下标”,快指针是老数组中的不需要删除的元素对应的下标

int slowIndex = 0;
for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
    if (val != nums[fastIndex]) {
        nums[slowIndex++] = nums[fastIndex];
    }
}
return slowIndex;

注意事项

1. 遍历的范围是0~nums.length-cnt
2. 进行覆盖之后需要注意i–

AC代码

class Solution {
    public int removeElement(int[] nums, int val) {
        int cnt=0;
        for (int i = 0; i < nums.length-cnt; i++) {
            if(nums[i]==val){
                for (int j = i; j <nums.length-1; j++) {
                    nums[j]=nums[j+1];
                }
                i--;
                cnt++;
            }
        }
        return nums.length-cnt;
    }
}

四、寻找插入位置

题目链接

思路

核心思路：二分查找/双指针

1. 如果在原数组中存在，直接返回对应的位置，此时就等价于上边的二分查找
2. 如果在元素中不存在，直接跳出循环，此时的left对应的下标恰好是对应的位置。

AC代码

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        int mid=left+(right-left)/2;
        while(left<=right){
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]>target){
                right=mid-1;
            }else{
                left=mid+1;
            }
            mid=left+(right-left)/2;
        }
        return left;
    }
}

五、总结

1. 数组在内存中是连续存储的，不能够实现物理意义上的删除，只能实现逻辑上的删除元素。
2. 逻辑删除元素的手段就是通过覆盖。
3. 二分查找题目中需要注意每次访问后都需要改变mid的值
4. 移除元素题目中需要注意每次覆盖后都需要i–，用于解决相邻待删除元素的问题，同时需要注意遍历的范围是在变化的。

二分法|二分查找法|二分搜索法|

二分易错点

1.while循环中的条件是left<right还是left<=right呢

2.当nums[mid]>target时，我们是更新左区间的右边界的，执行的操作是right=mid还是mid-1呢

相关概念

区间的类型

1. 左闭右闭
2. 左闭右开
3. 左开右闭

区间的类型决定了上边两个易错操作究竟怎么处理 。在处理的边界时，我们需要坚持不变量。一开始是半开半闭，处理出来的结果也必须是半开半闭，反之，必须是全闭区间。

代码实现

左闭右闭

1.left可以等于right

2. mid对应的大于target，那么应该是right=mid-1;

int left=0;
int right=nums.length-1;
int mid=left+(right-left)/2;
while(left<=right){
    if(nums[mid]==target){
        return mid;
    }else if(nums[mid]<target){
        left=mid+1;
    }else{
        right=mid-1;
    }
    mid=left+(right-left)/2;
}
return -1;

左闭右开

1. left不可以等于right【否则区间不合法】

2. mid对应的大于target，区间中本来就不包含mid,那么是right=mid就可以了;

int left=0;
int right=nums.length-1;
int mid=left+(right-left)/2;
while(left<right){
    if(nums[mid]==target){
        return mid;
    }else if(nums[mid]<target){
        left=mid;
    }else{
        right=mid;
    }
    mid=left+(right-left)/2;
}
return -1;