照射计算，是一种常用的三维几何计算。已知一个光源的光强图，计算光源投射到地表各处的功率密度。这种计算需求可以直观的理解为计算已知位置、指向、聚光特性的手电筒，计算地表某地点强度。

本文的推导涉及很多旋转，很容易出错和糊涂。当时刚刚毕业时，通宵推导、用Turbo C花了很大力气实现，结果笔记、程序都找不到了。现在已经白发丛生，从头重温一遍，也很是有趣。本推导可能存在符号反转等错误，等笔者后续做更有意思的场景时，不断验证才能更正。大家千万不要把这个代码真拿去仿真去了，十有八九会踩坑(-!

言归正传，为回答这个问题，需要进行几步描述。我们先解决单点测量问题：给定地表一点M，测量M位置的强度。

1 光源的强度

光源的远场强度特性，可以用一个三维矩阵来描述。上图中，假设在ECEF坐标系下，光源位于T点，其主轴为矢量 $\vec {TC}$ 。C是光源的轴线与地表的交点。假设地面有个观测点M，其与光源主轴的夹角为 $\alpha=\angle CTM$ 。同时，面TCM 与0度朝向面 TCA 的旋转夹角为 $\beta$ 。

则可以定义功率密度函数
$F(\alpha, \beta)$
来表示这个光源与全向光源之间的归一化增益密度。F的单位是 dBi，是该方向、距离上的等效全向辐射增益密度。需要格外强调的是，这种增益密度还需要与距离结合起来，才能计算出能量。此现象隐含着当光斑极为倾斜时，光斑上相同角度参数的部位，因为距离不同，能量的绝对值也不同。该值的意义参考电磁场弗里斯公式。

用这个函数可以生成方向图——一种极坐标形式的二维场强图。但二维场强图无法描述不规则的非对称场景，比如放在手电筒头部的广告画掩膜。这种掩膜经常被店铺用于在地表投射带有自身Logo的投影。在微波领域，由赋型波束形成的沿海岸线蜿蜒的照射区域也体现了高度的非对称性。因此，我们的计算还是需要基于函数F来做。这个F需要用户提供。

F参考的是一种极坐标系， $\alpha\beta D$ 坐标系，三个维度分别是轴夹角、转角、距离。

2 光源的指向

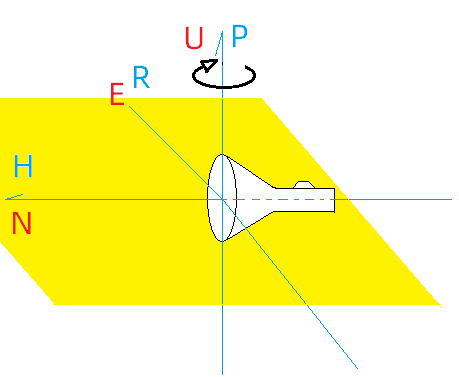
光源的指向，牵扯到另一个姿态坐标系- HPR 坐标系。这个坐标系以手电筒为原点，光源方向为H轴，轴线指向开关的方向为P轴，与H、P垂直的为R轴，如下图所示：

在之前的推导中，我们使用了 ENU 坐标系，也就是东北天，且定义方向是正北为0，顺时针递增。把手电筒的位置作为ENU的原点，在ENU坐标系的基础上，可以定义 HPR 的换算关系。

2.1 初始化HPR坐标系

为了在奇异角度下，比如正向下，保证矩阵的一致性，规定旋转前，手电开关朝上，平放于地面，指向正北。H轴与N重合，U轴与P重合，E轴与R重合，在ENU坐标下分别为

$\vec H=\{0_e,1_n,0_u\}, \vec P=\{0_e,0_n,1_u\}, \vec R=\{1_e,0_n,0_u\}$

在这里插入图片描述

为了后面计算方便，我们写成矩阵形式：

$T=\begin{bmatrix} {0_e}& {1_n} & {0_u }\\ {0_e} &{ 0_n} &{ 1_u }\\ {1_e}&{0_n} & {0_u} \end{bmatrix}$
上式中，矢量的列分别为E、N、U三个坐标，行是 H,P，R在ENU中的矢量。

2.2 引入旋转量

手电从初始状态开始，可在三维空间发生旋转，导致两个坐标系不再重合。要计算ENU坐标系下的点M在手电的本地坐标系HPR中的坐标，只需要计算H\P\R三个向量在ENU坐标系下的最终指向，而后把M与这组向量点积，得到的投影就是HPR坐标了。

手电筒的三维空间姿态，可描述为头部指向 (Heading)，俯仰（Pitch），横滚(Roll）。为了不出现混淆，规定施加三类旋转的顺序为H、P、R依次施加。

(1) Heading 朝向旋转

定义Heading角度 $h$ 为手电绕 $\vec P$ 矢量顺时针旋转的度数。注意，旋转后， $\vec H$ , $\vec R$ 都变化了，不再和 $\vec E$ 、 $\vec N$ 重合。

$H'=\{\sin h, \cos h,0\},\vec P=\{0,0,1\},R'=\{\cos h, -\sin h,0\}$

也就是

$T'=\begin{bmatrix} {0}& {1} & {0 }\\ {0} &{ 0} &{ 1 }\\ {1}&{0} & {0} \end{bmatrix} \times \begin{bmatrix} { \cos h}& { -\sin h} & {0 }\\ { \sin h} &{ \cos h} &{ 0 }\\ {0}&{0} & {1} \end{bmatrix}_H = \begin{bmatrix} \sin h & \cos h &0\\ {0} &{ 0} &{ 1 }\\ \cos h& -\sin h&0 \end{bmatrix}$

(2) Pitch 俯仰旋转

定义俯仰（Pitch） $p$ 是手电绕R旋转的度数:

$\vec H'=\{0,\cos p,-\sin p \}, \vec P'=\{0,\sin p,\cos p\}, \vec R=\{1,0,0\}$
$T'=\begin{bmatrix} {0}& {1} & {0 }\\ {0} &{ 0} &{ 1 }\\ {1}&{0} & {0} \end{bmatrix} \times \begin{bmatrix} 1&0&0\\ 0&\cos p & -\sin p\\ 0& \sin p&\cos p \end{bmatrix}_P = \begin{bmatrix} 0 & \cos p & -\sin p\\ 0 & \sin p & \cos p\\ 1&0&0 \end{bmatrix}$

（3）Roll 横滚旋转

定义横滚(Roll) $r$ 是在当前坐标下，绕 H 旋转的度数:

$\vec H=\{0,1,0\}, \vec P'=\{-\sin r ,0 ,\cos r \}, \vec R'=\{ \cos r ,0,\sin r\}$

$T'=\begin{bmatrix} {0}& {1} & {0 }\\ {0} &{ 0} &{ 1 }\\ {1}&{0} & {0} \end{bmatrix} \times \begin{bmatrix} \cos r&0&\sin r\\ 0&1&0\\ -\sin r&0& \cos r \end{bmatrix}_R = \begin{bmatrix} 0&1&0\\ -\sin r &0 & \cos r\\ \cos r &0&\sin r \end{bmatrix}$

2.3 从旋转到坐标系

有了上述定义，则可计算旋转后的坐标轴的向量。上文中，手电的初始坐标系在其ENU下的三个坐标轴的矢量如下：
$T_{enu}=\begin{bmatrix} {\vec H}\\ {\vec P}\\ {\vec R} \end{bmatrix}=\begin{bmatrix} {0}& {1} & {0 }\\ {0} &{ 0} &{ 1 }\\ {1}&{0} & {0} \end{bmatrix}$
则经过Heading旋转 $h$ 度、Pitch旋转 $p$ 度、翻滚 $r$ 度后，坐标轴变为：
$T'_{enu}=\begin{bmatrix} {0}& {1} & {0 }\\ {0} &{ 0} &{ 1 }\\ {1}&{0} & {0} \end{bmatrix}\times\left ( \begin{bmatrix} { \cos h}& { -\sin h} & {0 }\\ { \sin h} &{ \cos h} &{ 0 }\\ {0}&{0} & {1} \end{bmatrix}_H \times \begin{bmatrix} 1&0&0\\ 0&\cos p & -\sin p\\ 0& \sin p&\cos p \end{bmatrix}_P \times \begin{bmatrix} \cos r&0&\sin r\\ 0&1&0\\ -\sin r&0& \cos r \end{bmatrix}_R \right)$
经过化简：

$T'_{enu}=T_{enu}\times\begin{bmatrix} {\cos h \cos r-\sin h \sin p \sin r}& {-\sin h\cos p} & {\cos h \sin r + \sin h \sin p \cos r }\\ {\sin h \cos r + \cos h \sin p \sin r} &{ \cosh \cos p} &{ \sin h\sin r - \cos h \sin p \cos r }\\ {-\cos p \sin r} & {\sin p } & \cos p \cos r \end{bmatrix}_{T}$

该代码入口：

/*!
 * \brief hpr_T_from_hpr HPR 的三轴在ENU下的向量
 * \param hpr: Heading=h Pitch=p, Roll=r，小写的hpr是角度
 * \param T	: ENU下的HPR三轴向量。在旋转为0时， E=R N=H U=P。大写的HPR是笛卡尔坐标
 * \param rad 弧度true/度 false
 */
inline void hpr_T_in_enu(
	const double hpr[/*3*/],
	double T[/*3*/][3],
	const bool rad = false	);

因此，任意ENU坐标 $\vec M$ 在手电筒的坐标系里的坐标¹有如下转换关系：

$\vec M'^T_{HPR}=T'_{enu}\times M^T_{enu}$

$\vec M'^T_{enu}=T'^T_{enu}\times M^T_{HPR}$

主要入口:

/*!
 * \brief enu2HPR enu 笛卡尔坐标到 HPR 笛卡尔坐标。注意，大写HPR是坐标不是角度。
 * \param T		HPR 的三轴在ENU下的向量，由hpr_T_in_enu生成
 * \param A_enu	enu坐标矢量
 * \param A_HPR	HPR坐标矢量
 */
inline void enu2HPR(
	const double T[/*3*/][3],
	const double A_enu[/*3*/],
	double A_HPR[/*3*/]);
/*!
 * \brief HPR2enu  HPR 笛卡尔坐标到 enu笛卡尔坐标。注意，大写HPR是坐标不是角度。
 * \param T		HPR 的三轴在ENU下的向量，由hpr_T_in_enu生成
 * \param A_HPR	HPR坐标矢量
 * \param A_enu	enu坐标矢量
 */
inline void HPR2enu(
	const double T[/*3*/][3],
	const double A_HPR[/*3*/],
	double A_enu[/*3*/]);

T矩阵也是一类正交矩阵，逆就是转置。通过上述变换，能够把本篇的测量点M的坐标，依次转 ECEF, ENU, HPR，变成以手电筒的本地HPR坐标系为参考的位置，以便求取 $F(\alpha, \beta)$ 需要的角度、距离。

3 联合求解

3.1 M的 $\alpha\beta D$ 坐标

当测试点M的HPR坐标已知后，可以根据几何关系直接确定角度、距离。
$D=\sqrt{H^2+P^2+R^2}$

$\tan \beta=-\frac{R}{P}$

$\cos \alpha=\frac{H}{D}$

范例:

void demo_cover()
{
	using namespace CES_GEOCALC;
	//光源的LLA
	const double lla_torch [3] = {35.273, 117.121, 17500};
	//光源的姿态角度
	const double hpr_torch [3] = {135,45,-30};
	double T_torch[3][3] = {0,0,0,0,0,0,0,0,0};
	hpr_T_in_enu(hpr_torch,T_torch);
	//光源 ECEF
	double ecef_torch[3] = {0,0,0};
	lla2ecef(lla_torch,ecef_torch);
	//光源ENU
	double R_torch[3][3] = {0,0,0,0,0,0,0,0,0};
	enu_R_from_lla(lla_torch,R_torch);


	//M 的LLA、ECEF
	const double lla_M [3] = {34.773, 117.621, 265};
	double ecef_M[3] = {0,0,0};
	lla2ecef(lla_M,ecef_M);
	//M 在光源ENU中的坐标
	double enu_M[3]={0,0,0};
	ecef2enu(R_torch,ecef_torch,ecef_M,enu_M);

	//M 在光源 HPR中的坐标
	double hpr_M[3] = {0,0,0};
	enu2HPR(T_torch,enu_M,hpr_M);

	//alpha beta D
	const double H = hpr_M[0], P=hpr_M[1], R=hpr_M[2];
	const double D = sqrt(H*H+P*P+R*R);
	const double alpha = rad2deg * acos(H/D);
	const double beta = rad2deg * ((P>=-1e-10 && P<1e-10 && R>=-1e-10 && R<1e-10 )?0:-atan2(R,P));

	printf ("D=%lf,Alpha=%lf,Beta=%lf\n",D,alpha,beta);
}