https://www.luogu.com.cn/problem/P3803

• 傅里叶变换(FFT)笔记存档
• FFT代码上的实现细节

主函数

1. 把长度设为2的整数次幂块
   

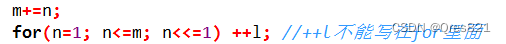
2. 初始进行翻转（二进制翻转）
   

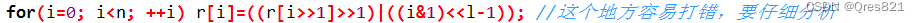
3. 对A，B先化为点值（DFT）
   

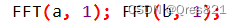
4. 相乘

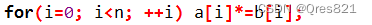
5. IDFT

FFT函数

1. 进行初始翻转：

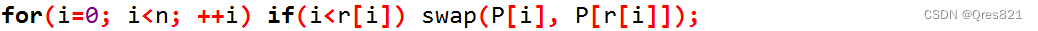2. 枚举区间长度，并计算单位根

3. 逐个枚举区间（哪个区间），每个区间内部也进行枚举
   4. 区间内部进行分治合并

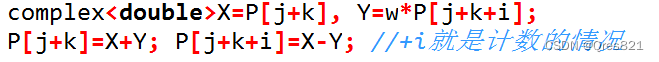
$i$：半块长

完整code

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//#define M
//#define mo
#define N 3000010
#define Pi acos(-1)
int n, m, i, j, k, T;
complex<double>a[N], b[N]; 
int r[N], l; 

void FFT(complex<double>*P, int op) {
	for(i=0; i<n; ++i) if(i<r[i]) swap(P[i], P[r[i]]); 
	for(i=1; i<n; i<<=1) { // 当前分治区间长度为 2i
		complex<double>W(cos(Pi/i), sin(Pi/i)*op); 
		for(j=0; j<n; j+=(i<<1)) { // 注意加的是区间长度，这一维枚举的是哪个区间 
			complex<double>w(1, 0); 
			for(k=0; k<i; ++k, w*=W) { //枚举每个区间内部 ，枚举到 i其实相当于只枚举了一半 
				complex<double>X=P[j+k], Y=w*P[j+k+i]; 
				P[j+k]=X+Y; P[j+k+i]=X-Y; //+i就是计数的情况 
			}
		}
	}
}

signed main()
{
//	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);
//	srand(time(NULL));
//	T=read();
//	while(T--) {
//
//	}
	n=read(); m=read(); 
	for(i=0; i<=n; ++i) a[i]=read(); 
	for(i=0; i<=m; ++i) b[i]=read(); 
	m+=n; 
	for(n=1; n<=m; n<<=1) ++l; //++l不能写在for里面 
	for(i=0; i<n; ++i) r[i]=((r[i>>1]>>1)|((i&1)<<l-1)); //这个地方容易打错，要仔细分析 
	FFT(a, 1); FFT(b, 1);  
	for(i=0; i<n; ++i) a[i]*=b[i]; 
	FFT(a, -1); 
	for(i=0; i<=m; ++i) printf("%lld ", (int)(a[i].real()/n+0.5)); 
	return 0;
}