基于二分查找的拓展问题

1.山脉数组的峰顶索引

思路：二分查找

山峰有三种状态：需要注意数组边界

1.顶峰：arr[mid]>arr[mid+1]&&arr[mid]>arr[mid-1]

2.上坡：arr[mid]<arr[mid+1]

3.下坡：arr[mid] < arr[mid-1]

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int left = 0;
        int right = arr.length-1;
        while(left<=right){
            int mid = left + ((right - left)>>1);
            if(mid == 0 && mid == arr.length-1){
                return -1;
            }
            if(arr[mid]>arr[mid+1]&&arr[mid]>arr[mid-1]){
                return mid;
            }else if(arr[mid]<arr[mid+1]){
                left = mid + 1;
            }else if(arr[mid] < arr[mid-1]){
                right = mid - 1;
            }
        }
        return -1;
    }
}

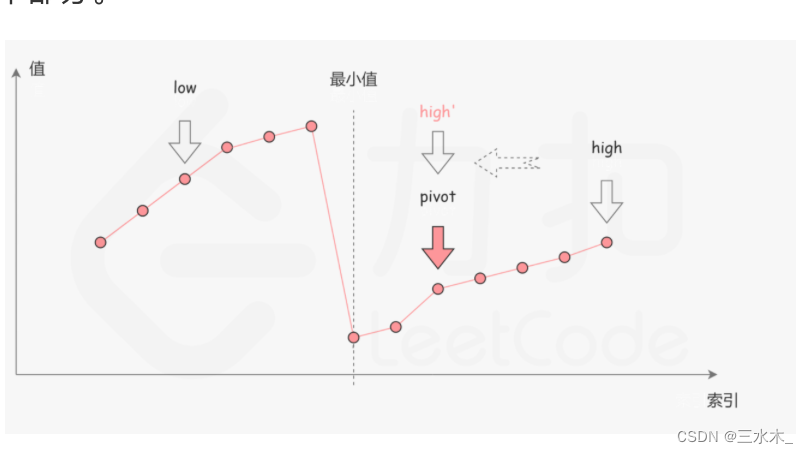
2.寻找旋转排序数组中的最小值

 思路：抓住目标值nums[mid]一定是小于等于nums[high]

class Solution {
    public int findMin(int[] nums) {
        int l = 0;
        int r = nums.length - 1;
        int mid = 0;
        while(l<r){
            mid = l + ((r-l)>>1);
            if(nums[mid]>=nums[r]){
                l = mid + 1;
            }else if(nums[mid]<nums[r]){
                r = mid;
            }
        }
        return nums[l];
    }
}

3.寻找旋转排序数组中的最小值II

思路：

本题含有重复的元素

[1,3,3]这种情况，就不能单纯的判断nums[mid]>=nums[high]就舍弃当前mid左区间

但是还是抓住nums[mid]一定是小于等于nums[high]关键，也就是一定在high左边

当nums[mid]==nums[high]，high--缩小范围

class Solution {
    public int findMin(int[] nums) {
        int l = 0;
        int r = nums.length - 1;
        int mid = 0;
        while(l<r){
            mid = l + ((r-l)>>1);
            if(nums[mid]>nums[r]){
                l = mid + 1;
            }else if(nums[mid]<nums[r]){
                r = mid;
            }else{
                r -= 1;
            }
        }
        return nums[l];
    }
}

 4.缺失的数字

思路： 二分查找思路，递增数组

一般情况nums[mid]==mid说明缺失值在mid右侧

nums[mid]>mid，说明缺失值在mid左侧

class Solution {
    public int missingNumber(int[] nums) {
        int low = 0;
        int high = nums.length - 1;
        while(low<=high){
            int mid = low + ((high - low)>>1);
            if(nums[mid]>mid){
                high = mid-1;
            }else if(nums[mid]==mid){
                low = mid+1;
            }
        }
        return low;
    }
}

5.x的平方根

思路：二分思想，需要注意超过int范围的情况不能直接乘

class Solution {
    public int mySqrt(int x) {
        if(x <= 1){
            return x;
        }
        int low = 0;
        int high = x;
        while(low<high){
            int mid = low + ((high - low)>>1);
            if(x/mid == mid){
                return mid;
            }else if(x/mid<mid){
                high = mid;
            }else{
                low = mid+1;
            }
        }
        return low-1;
    }
}

中序和搜索树

二叉搜索树：左结点小于根结点，右结点大于根结点

二叉搜索树的中序遍历从小到大递增

1.二叉搜索树中的搜索

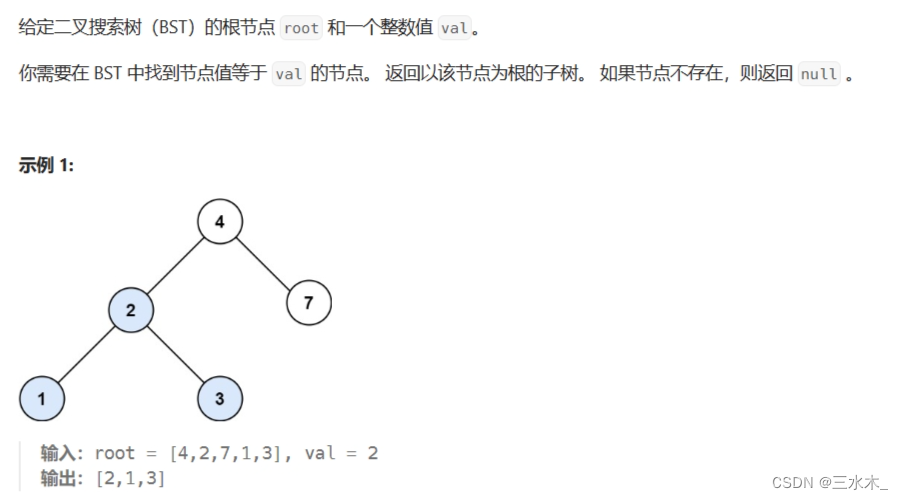
思路：很简单，与根结点比较，小于往左大于往右，等于返回 。

二叉树递归方法参考二叉树经典算法题

按照递归三部曲写出递归函数，迭代也是可以的。

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root == null){
            return null;
        }
        if(root.val > val){
            return searchBST(root.left,val);
        }
        if(root.val < val){
            return searchBST(root.right,val);
        }
        return root;
    }
}

2.验证二叉搜索树

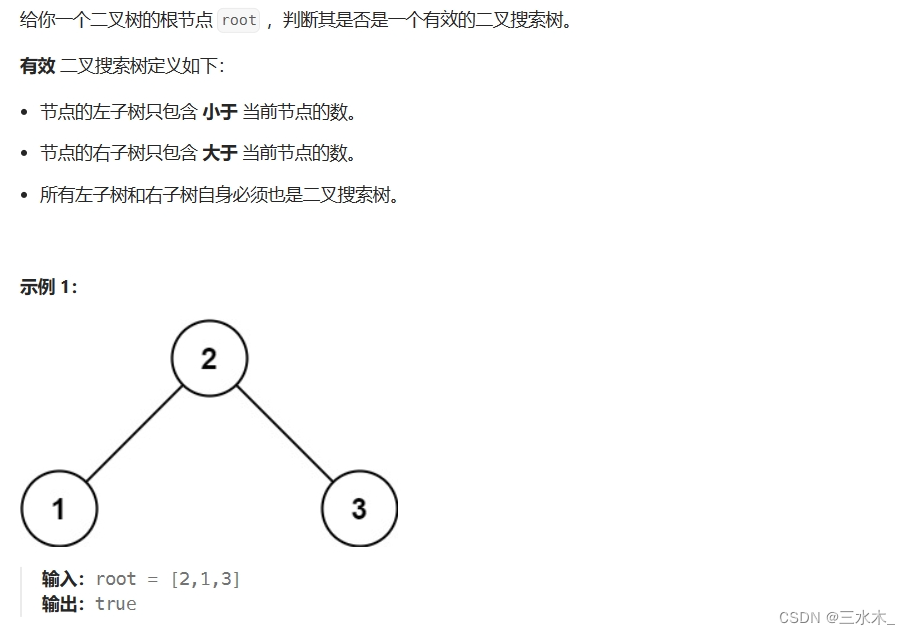
思路：利用搜索树中序遍历递增的特性，如果出现小于前一个值的情况就返回false

class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if(root == null){
            return true;
        }
        boolean left = isValidBST(root.left);
        if(root.val<=pre){
            return false;
        }
        pre = root.val;
        boolean right = isValidBST(root.right);
        return left&&right;
    }
}