1 引言

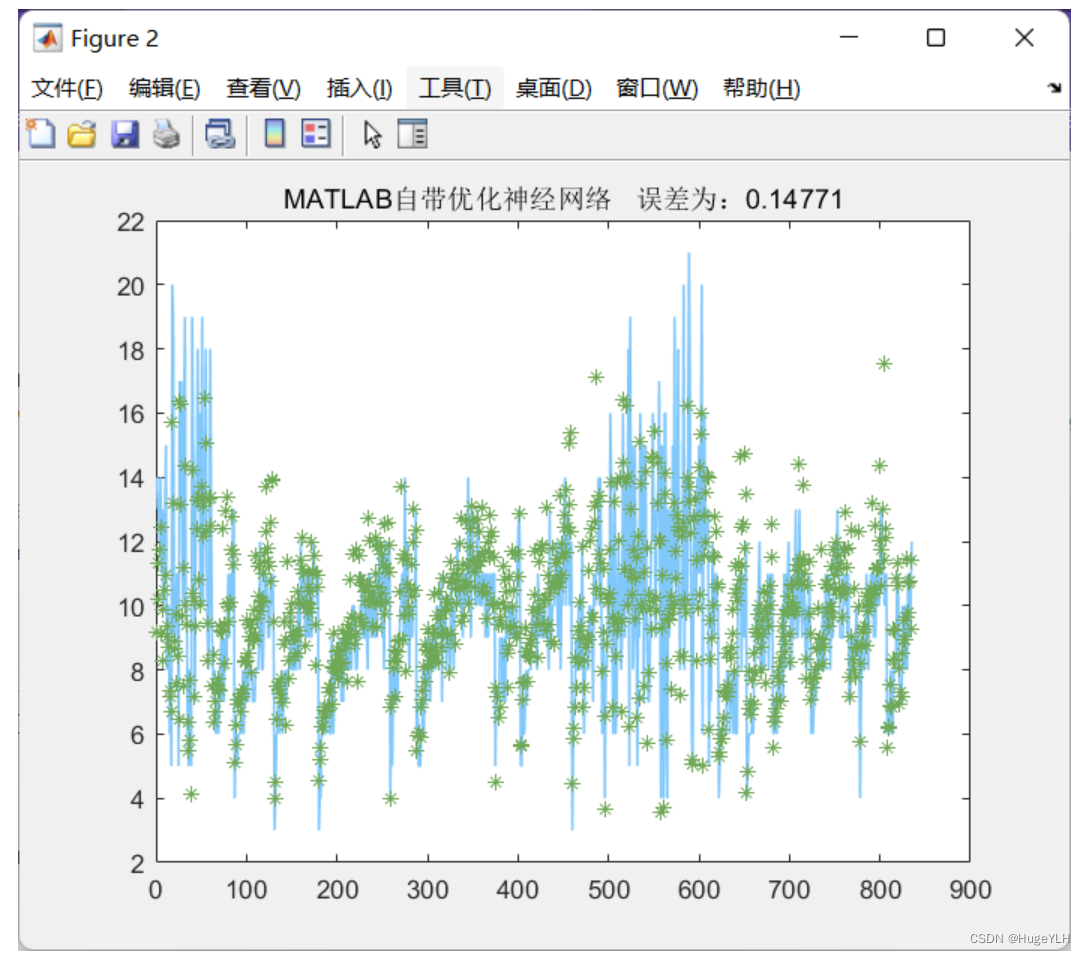
在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SELU、GELU、Softmax、Softplus、Mish、Maxout、HardSigmoid、HardTanh、Hardswish、HardShrink、SoftShrink、TanhShrink、RReLU、CELU、ReLU6、GLU、SwiGLU、GTU、Bilinear、ReGLU、GEGLU、Softmin、Softmax2d、Logsoftmax、Identity、LogSigmoid、Bent Identity、Absolute、Bipolar、Bipolar Sigmoid、Sinusoid、Cosine、Arcsinh、Arccosh、Arctanh、LeCun Tanh、TanhExp、Gaussian 、GCU、ASU、SQU、NCU、DSU、SSU、SReLU、BReLU、PELU、Phish、RBF、SQ-RBF、ISRU、ISRLU、SQNL、PLU、APL、Inverse Cubic、Soft Exponential、ParametricLinear)。在这篇文章中，会接着上文提到的众多激活函数继续进行介绍，给大家带来更多不常见的激活函数的介绍。这里放一张激活函数的机理图：
在这里插入图片描述

2 激活函数

2.1 Piecewise Linear Unit激活函数

论文链接：https://arxiv.org/abs/2104.03693

Piecewise Linear Unit分段激活函数，通过公式设计+可学习参数的方式，来达到算法SOTA的结果。其数学表达式和数学图像分别如下所示：
$\begin{cases} (x-B_L)*K_L+Y_P^0, & \text{if } x<B_L \\ (x-B_R)*K_R+Y_P^N, & \text{if } x \geq B_R \\ (x-B_{idx})*K_{idx}+Y_P^{idx}, & \text{if }B_L \leq x < B_R\\ \end{cases}$ 在这里插入图片描述
其中，在 $B_L, B_R]$ 间被划分为 N 段，每一段都有其自己的斜率。

特性：(参考自：Piecewise Linear Unit：分段线性激活函数)

PWLU可以表示任意连续，有边界的scalar function
PWLU变换连续，利于求导
可以最大限度利用可学习参数
由于我们划分段是N等分的，所以在计算，推理中是efficient的

优点：

灵活性： “Piecewise Linear” 激活函数允许在不同区间内使用不同的线性函数，从而适应不同的数据模式和分布。
逼近复杂性： 通过合理设置划分区间和线性函数的参数，这种激活函数能够逼近一些复杂的非线性特性。
可解释性： 由于它由多个线性段组成，其行为相对容易解释，参数的含义也相对明确。

缺点：

参数设置： 需要仔细选择划分区间、斜率和截距参数，以获得良好的性能。不恰当的参数设置可能会导致模型表现不佳。
有限的表达能力： 尽管能够逼近一些非线性特性，但在某些复杂问题中，可能仍然无法捕捉到更深层次的非线性模式。
计算开销： 需要根据划分区间的数量执行不同的线性函数计算，可能在计算上增加一定的开销。

虽然作者提出Piecewise Linear Unit是为了让激活函数逼近和表达出各种性质且表现出了很好的性质，但是论文代码仍为开源，当前仍未广泛使用。。。。。

2.2 Complementary Log-Log (CLL)激活函数

论文链接：Gomes, Gecynalda S. da S., and Teresa B. Ludermir. “Complementary log-log and probit: activation functions implemented in artificial neural networks.” In 2008 Eighth International Conference on Hybrid Intelligent Systems, pp. 939-942. IEEE, 2008.

Complementary Log-Log（CLL）激活函数是一种非常特殊的激活函数，通常用于极端稀疏数据的建模。它在广义线性模型（Generalized Linear Models，GLMs）和某些神经网络中被用作连接函数（link function），用于将线性输出映射到正实数范围。其数学表达式和数学图像分别如下所示：
$f(x)=1-e^{-e^x}$ 在这里插入图片描述
优点：