摘要: 本贴从零开始学习正演的数值模拟方法. 包括相应的偏微分基础、声波方程、雷克子波、均匀速度场的模拟、一般速度场的模拟.
1. 偏微分基础
本小节仅涉及高等数学相关知识, 与领域无关.
1.1 导数
引例: 物体从一维坐标的原点开始移动, 在
t
t
t 时刻, 它在坐标轴的位置由函数
s
(
t
)
s(t)
s(t) 确定, 则速度为位置变化量与时间的比值:
v
(
t
)
=
d
s
(
t
)
d
t
=
lim
Δ
t
→
0
s
(
t
+
Δ
t
)
−
s
(
t
)
Δ
t
(1)
v(t) = \frac{\mathrm{d} s(t)}{\mathrm{d} t} = \lim_{\Delta t \to 0} \frac{s(t + \Delta t) - s(t)}{\Delta t} \tag{1}
v(t)=dtds(t)=Δt→0limΔts(t+Δt)−s(t)(1)
加速度为速度变化量与时间的比值:
a
(
t
)
=
d
v
(
t
)
d
t
=
lim
Δ
t
→
0
v
(
t
)
−
v
(
t
−
Δ
t
)
Δ
t
=
lim
Δ
t
→
0
s
(
t
+
Δ
t
)
−
2
s
(
t
)
+
s
(
t
−
Δ
t
)
Δ
t
2
(2)
a(t) = \frac{\mathrm{d} v(t)}{\mathrm{d} t} = \lim_{\Delta t \to 0} \frac{v(t) - v(t - \Delta t)}{\Delta t} = \lim_{\Delta t \to 0} \frac{s(t + \Delta t) - 2 s(t) + s(t - \Delta t)}{\Delta t^2} \tag{2}
a(t)=dtdv(t)=Δt→0limΔtv(t)−v(t−Δt)=Δt→0limΔt2s(t+Δt)−2s(t)+s(t−Δt)(2)
推广 1: 给定一个单变量函数
y
=
f
(
x
)
(3)
y = f(x) \tag{3}
y=f(x)(3)
其一阶导数记为
y
′
=
d
f
(
x
)
d
x
(4)
y' = \frac{\mathrm{d} f(x)}{\mathrm{d} x} \tag{4}
y′=dxdf(x)(4)
二阶导数记为
y
′
′
=
d
2
f
(
x
)
d
x
2
(5)
y'' = \frac{\mathrm{d}^2 f(x)}{\mathrm{d} x^2} \tag{5}
y′′=dx2d2f(x)(5)
1.2 偏导
给定一个二变量函数
z
=
f
(
x
,
y
)
(6)
z = f(x, y) \tag{6}
z=f(x,y)(6)
其针对
x
x
x 偏导的为
∂
z
∂
x
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
,
y
)
−
f
(
x
,
y
)
Δ
x
(7)
\frac{\partial z}{\partial x} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x, y) - f(x, y)}{\Delta x} \tag{7}
∂x∂z=Δx→0limΔxf(x+Δx,y)−f(x,y)(7)
即
x
x
x 发生了变化, 而
y
y
y 并没变化.
进一步, 二阶偏导为
∂
2
z
∂
x
2
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
,
y
)
−
f
(
x
,
y
)
Δ
x
−
f
(
x
,
y
)
−
f
(
x
−
Δ
x
,
y
)
Δ
x
Δ
x
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
,
y
)
−
2
f
(
x
,
y
)
+
f
(
x
−
Δ
x
,
y
)
Δ
x
2
(8)
\begin{array}{ll}\frac{\partial^2 z}{\partial x^2} &= \lim_{\Delta x \to 0} \frac{\frac{f(x + \Delta x, y) - f(x, y)}{\Delta x} - \frac{f(x, y) - f(x - \Delta x, y)}{\Delta x} }{\Delta x} \\ & = \lim_{\Delta x \to 0} \frac{f(x + \Delta x, y) - 2 f(x, y) + f(x - \Delta x, y)}{\Delta x^2} \end{array}\tag{8}
∂x2∂2z=limΔx→0ΔxΔxf(x+Δx,y)−f(x,y)−Δxf(x,y)−f(x−Δx,y)=limΔx→0Δx2f(x+Δx,y)−2f(x,y)+f(x−Δx,y)(8)
另外有 (这两个式子在本贴里面不用, 写着让大家复习):
∂
2
z
∂
x
∂
y
=
lim
Δ
x
→
0
,
Δ
y
→
0
f
(
x
+
Δ
x
,
y
+
Δ
y
)
−
f
(
x
,
y
+
Δ
y
)
−
f
(
x
+
Δ
x
,
y
)
+
f
(
x
,
y
)
Δ
x
Δ
y
(9)
\frac{\partial^2 z}{\partial x \partial y} = \lim_{\Delta x \to 0, \Delta y \to 0} \frac{f(x + \Delta x, y + \Delta y) - f(x, y + \Delta y) - f(x + \Delta x, y) + f(x, y)}{\Delta x \Delta y} \tag{9}
∂x∂y∂2z=Δx→0,Δy→0limΔxΔyf(x+Δx,y+Δy)−f(x,y+Δy)−f(x+Δx,y)+f(x,y)(9)
∂
2
z
∂
y
∂
x
=
∂
2
z
∂
x
∂
y
(10)
\frac{\partial^2 z}{\partial y \partial x} = \frac{\partial^2 z}{\partial x \partial y} \tag{10}
∂y∂x∂2z=∂x∂y∂2z(10)
在进行数值模拟的时候, 不可能取
Δ
x
→
0
\Delta x \to 0
Δx→0, 因此 (8) 式简化为
∂
2
z
∂
x
2
≈
f
(
x
+
Δ
x
,
y
)
−
2
f
(
x
,
y
)
+
f
(
x
−
Δ
x
,
y
)
Δ
x
2
(11)
\frac{\partial^2 z}{\partial x^2} \approx \frac{f(x + \Delta x, y) - 2 f(x, y) + f(x - \Delta x, y)}{\Delta x^2} \tag{11}
∂x2∂2z≈Δx2f(x+Δx,y)−2f(x,y)+f(x−Δx,y)(11)
注 1: 为统一起见, 即使一元函数, 以后也常使用 ∂ \partial ∂ 而不是 d \mathrm{d} d.
1.3 泰勒级数
显然,
Δ
x
\Delta x
Δx 越接近
0
0
0 误差就越小, 但在实际地震数据采集中, 需要的设备就越多. 例如,
Δ
=
5
m
\Delta = 5 \mathrm{m}
Δ=5m, 即每隔 5m 放置一个检波器, 就要花费
Δ
=
20
m
\Delta = 20 \mathrm{m}
Δ=20m 时 4 倍的成本, 需要计算的网格点数也增加到后者的 16 倍 (2 维剖面) 或 64 倍 (3 维数据体).
从 (11) 式, 我们无法知道: 这个约等于究竟涉及多大的误差?
为了确切知道误差在哪个量级之内, 我们需要引入更高级的数学工具: 泰勒级数.
当函数
f
(
x
)
f(x)
f(x) 在
x
0
x_0
x0 处存在直到
n
n
n 阶的导数, 则
f
(
x
)
=
f
(
x
0
)
+
∑
i
=
1
n
f
(
i
)
(
x
0
)
(
x
−
x
0
)
i
i
!
+
o
(
(
x
−
x
0
)
n
)
(12)
f(x) = f(x_0) + \sum_{i = 1}^n \frac{f^{(i)}(x_0)(x - x_0)^i}{i!} + o((x - x_0)^n) \tag{12}
f(x)=f(x0)+i=1∑ni!f(i)(x0)(x−x0)i+o((x−x0)n)(12)
其中
f
(
i
)
(
x
0
)
/
i
!
f^{(i)}(x_0) / i!
f(i)(x0)/i! 称为泰勒展开式的系数.
直观的解释: 如果函数
f
(
x
)
f(x)
f(x) 不是线性的, 则它的变化量不仅与斜率有关, 而且与斜率的变化率也有关. 更多内容就只有自己去找数学书啃了.
为与我们前面的内容相符, 将 (12) 式
x
0
x_0
x0 记作
x
x
x,
x
x
x 记作
x
+
Δ
x
x + \Delta x
x+Δx, 得到
f
(
x
+
Δ
x
)
=
f
(
x
)
+
∑
i
=
1
n
f
(
i
)
(
x
)
Δ
x
i
i
!
+
o
(
Δ
x
n
)
(13)
f(x + \Delta x) = f(x) + \sum_{i = 1}^n \frac{f^{(i)}(x) \Delta x^i}{i!} + o(\Delta x^n) \tag{13}
f(x+Δx)=f(x)+i=1∑ni!f(i)(x)Δxi+o(Δxn)(13)
为方便学计算机的同学理解, 来讲几个特例. 数学学院的同学忽略.
例 1. 验证二次函数
f
(
x
)
=
a
x
2
+
b
(14)
f(x) = a x^2 + b \tag{14}
f(x)=ax2+b(14)
f
(
x
+
Δ
x
)
=
(
a
x
2
+
b
)
+
2
a
x
Δ
x
+
2
a
Δ
x
2
/
2
=
a
x
2
+
2
a
x
Δ
x
+
a
Δ
x
2
+
b
=
a
(
x
+
Δ
x
)
2
+
b
f(x + \Delta x) = (a x^2 + b) + 2ax \Delta x + 2a \Delta x^2/2 = ax^2 + 2ax \Delta x + a \Delta x^2 + b = a(x + \Delta x)^2 + b
f(x+Δx)=(ax2+b)+2axΔx+2aΔx2/2=ax2+2axΔx+aΔx2+b=a(x+Δx)2+b
验证结束.
注意: 泰勒级数现实的意义不在于这种一直连续可导的函数, 而是在某些区域可导的函数.
1.4 2 阶精度
我们不知道
n
n
n 的具体取值, 就会假设它比较大. 在数值计算的时候, 会忽略 (13) 式的
o
(
Δ
x
n
)
o(\Delta x^n)
o(Δxn) 甚至前面某些累加式. 也就是说, 假设存在 10 阶导数, 但我们仅取
n
=
2
n = 2
n=2 的话, 误差就被控制在
o
(
Δ
x
2
)
o(\Delta x^2)
o(Δx2), 这时候称为 2 阶精度. 仅取
n
=
4
n = 4
n=4 的话, 误差就被控制在
o
(
Δ
x
4
)
o(\Delta x^4)
o(Δx4), 这时候称为 4 阶精度. 显然, 4 阶精度比 2 阶精度省略的值更小, 因此精度更高. 我们可以根据自己的需求, 设置相应的精度. 在地震数据数值模拟中,
n
+
2
n + 2
n+2 阶比
n
n
n 阶的误差大概低 1 个数量级. 正演模拟在传播过程中误差会不断累积, 严重的情况下出现“频散” (不应该存在的波, 见图 3), 所以我们还是倾向于多计算一些.
特别地, 仅考虑 2 阶精度的时候
f
(
x
+
Δ
x
)
=
f
(
x
)
+
∂
f
∂
x
Δ
x
+
∂
2
f
∂
x
2
Δ
x
2
2
+
o
(
Δ
x
2
)
(15)
f(x + \Delta x) = f(x) + \frac{\partial f}{\partial x} \Delta x + \frac{\partial^2 f}{\partial x^2} \frac{\Delta x^2}{2} + o(\Delta x^2) \tag{15}
f(x+Δx)=f(x)+∂x∂fΔx+∂x2∂2f2Δx2+o(Δx2)(15)
将 (15) 式移项得到
f
(
x
+
Δ
x
)
−
f
(
x
)
=
∂
f
∂
x
Δ
x
+
∂
2
f
∂
x
2
Δ
x
2
2
+
o
(
Δ
x
2
)
(16)
f(x + \Delta x) - f(x)= \frac{\partial f}{\partial x} \Delta x + \frac{\partial^2 f}{\partial x^2} \frac{\Delta x^2}{2} + o(\Delta x^2) \tag{16}
f(x+Δx)−f(x)=∂x∂fΔx+∂x2∂2f2Δx2+o(Δx2)(16)
同理得到
f
(
x
)
−
f
(
x
−
Δ
x
)
=
∂
f
∂
x
Δ
x
−
∂
2
f
∂
x
2
Δ
x
2
2
+
o
(
Δ
x
2
)
(17)
f(x) - f(x - \Delta x)= \frac{\partial f}{\partial x} \Delta x - \frac{\partial^2 f}{\partial x^2} \frac{\Delta x^2}{2} + o(\Delta x^2) \tag{17}
f(x)−f(x−Δx)=∂x∂fΔx−∂x2∂2f2Δx2+o(Δx2)(17)
这里
o
(
Δ
x
2
)
o(\Delta x^2)
o(Δx2) 的符号可正可负.
(16) 式减去 (17) 式, 然后将两边同时除以
Δ
x
2
\Delta x^2
Δx2 可得
∂
2
f
∂
x
2
=
f
(
x
+
Δ
x
)
−
2
f
(
x
)
+
f
(
x
−
Δ
x
)
Δ
x
2
+
O
(
Δ
x
2
)
(18)
\frac{\partial^2 f}{\partial x^2} = \frac{f(x + \Delta x) - 2 f(x) + f(x - \Delta x)}{\Delta x^2} + O(\Delta x^2) \tag{18}
∂x2∂2f=Δx2f(x+Δx)−2f(x)+f(x−Δx)+O(Δx2)(18)
这里的高阶无穷小除了相应的变量后, 成为同阶无穷小.
注 2: 奇数阶精度不用计算, 例如 3 阶与 2 阶精度的表达式是一样的, 仅把
O
(
Δ
x
2
)
O(\Delta x^2)
O(Δx2) 替换为
O
(
Δ
x
3
)
O(\Delta x^3)
O(Δx3) 即可.
1.5 4 阶精度
考虑到 4 阶导数的时候
f
(
x
+
Δ
x
)
=
f
(
x
)
+
∂
f
∂
x
Δ
x
+
∂
2
f
∂
x
2
Δ
x
2
2
+
∂
3
f
∂
x
3
Δ
x
3
6
+
∂
4
f
∂
x
4
Δ
x
4
24
+
o
(
Δ
x
4
)
(19)
f(x + \Delta x) = f(x) + \frac{\partial f}{\partial x} \Delta x + \frac{\partial^2 f}{\partial x^2} \frac{\Delta x^2}{2} + \frac{\partial^3 f}{\partial x^3} \frac{\Delta x^3}{6} + \frac{\partial^4 f}{\partial x^4} \frac{\Delta x^4}{24}+ o(\Delta x^4) \tag{19}
f(x+Δx)=f(x)+∂x∂fΔx+∂x2∂2f2Δx2+∂x3∂3f6Δx3+∂x4∂4f24Δx4+o(Δx4)(19)
f
(
x
+
Δ
x
)
−
f
(
x
)
=
∂
f
∂
x
Δ
x
+
∂
2
f
∂
x
2
Δ
x
2
2
+
∂
3
f
∂
x
3
Δ
x
3
6
+
∂
4
f
∂
x
4
Δ
x
4
24
+
o
(
Δ
x
4
)
(20)
f(x + \Delta x) - f(x) = \frac{\partial f}{\partial x} \Delta x + \frac{\partial^2 f}{\partial x^2} \frac{\Delta x^2}{2} + \frac{\partial^3 f}{\partial x^3} \frac{\Delta x^3}{6} + \frac{\partial^4 f}{\partial x^4} \frac{\Delta x^4}{24}+ o(\Delta x^4) \tag{20}
f(x+Δx)−f(x)=∂x∂fΔx+∂x2∂2f2Δx2+∂x3∂3f6Δx3+∂x4∂4f24Δx4+o(Δx4)(20)
f
(
x
)
−
f
(
x
−
Δ
x
)
=
∂
f
∂
x
Δ
x
−
∂
2
f
∂
x
2
Δ
x
2
2
+
∂
3
f
∂
x
3
Δ
x
3
6
−
∂
4
f
∂
x
4
Δ
x
4
24
+
o
(
Δ
x
4
)
(21)
f(x) - f(x - \Delta x)= \frac{\partial f}{\partial x} \Delta x - \frac{\partial^2 f}{\partial x^2} \frac{\Delta x^2}{2} + \frac{\partial^3 f}{\partial x^3} \frac{\Delta x^3}{6} - \frac{\partial^4 f}{\partial x^4} \frac{\Delta x^4}{24}+ o(\Delta x^4) \tag{21}
f(x)−f(x−Δx)=∂x∂fΔx−∂x2∂2f2Δx2+∂x3∂3f6Δx3−∂x4∂4f24Δx4+o(Δx4)(21)
(20) 式减去 (21) 式, 然后将两边同时除以
Δ
x
2
\Delta x^2
Δx2 可得
∂
2
f
∂
x
2
=
f
(
x
+
Δ
x
)
−
2
f
(
x
)
+
f
(
x
−
Δ
x
)
Δ
x
2
−
∂
4
f
∂
x
4
Δ
x
2
12
+
o
(
Δ
x
2
)
(22)
\frac{\partial^2 f}{\partial x^2} = \frac{f(x + \Delta x) - 2 f(x) + f(x - \Delta x)}{\Delta x^2} - \frac{\partial^4 f}{\partial x^4} \frac{\Delta x^2}{12}+ o(\Delta x^2) \tag{22}
∂x2∂2f=Δx2f(x+Δx)−2f(x)+f(x−Δx)−∂x4∂4f12Δx2+o(Δx2)(22)
将
Δ
x
\Delta x
Δx 换为
2
Δ
x
2 \Delta x
2Δx, 同理可得
∂
2
f
∂
x
2
=
f
(
x
+
2
Δ
x
)
−
2
f
(
x
)
+
f
(
x
−
2
Δ
x
)
4
Δ
x
2
−
∂
4
f
∂
x
4
16
Δ
x
2
12
+
o
(
Δ
x
2
)
(23)
\frac{\partial^2 f}{\partial x^2} = \frac{f(x + 2\Delta x) - 2 f(x) + f(x - 2\Delta x)}{4 \Delta x^2} - \frac{\partial^4 f}{\partial x^4} \frac{16 \Delta x^2}{12} + o(\Delta x^2) \tag{23}
∂x2∂2f=4Δx2f(x+2Δx)−2f(x)+f(x−2Δx)−∂x4∂4f1216Δx2+o(Δx2)(23)
(22) 式乘以 16 减去 (23) 式, 可得
∂
2
f
∂
x
2
=
16
15
f
(
x
+
Δ
x
)
−
2
f
(
x
)
+
f
(
x
−
Δ
x
)
Δ
x
2
−
1
15
f
(
x
+
2
Δ
x
)
−
2
f
(
x
)
+
f
(
x
−
2
Δ
x
)
4
Δ
x
2
+
O
(
Δ
x
4
)
(24)
\frac{\partial^2 f}{\partial x^2} = \frac{16}{15}\frac{f(x + \Delta x) - 2 f(x) + f(x - \Delta x)}{\Delta x^2} - \frac{1}{15}\frac{f(x + 2\Delta x) - 2 f(x) + f(x - 2\Delta x)}{4 \Delta x^2}+ O(\Delta x^4) \tag{24}
∂x2∂2f=1516Δx2f(x+Δx)−2f(x)+f(x−Δx)−1514Δx2f(x+2Δx)−2f(x)+f(x−2Δx)+O(Δx4)(24)
从这里可以看到, 通过引入
2
Δ
x
2 \Delta x
2Δx, 可以消去 4 阶偏导. 这是增加精度的核心技巧.
1.6 2 n 2n 2n 阶精度
通过前面的“核心技巧”, 将 (24) 式进一步推广, 可得
2
n
2n
2n 阶精度的表达式
∂
2
f
∂
x
2
=
∑
i
=
1
n
(
−
1
)
i
+
1
c
i
f
(
x
+
i
Δ
x
)
−
2
f
(
x
)
+
f
(
x
−
i
Δ
x
)
i
2
Δ
x
2
+
O
(
Δ
x
2
n
)
(25)
\frac{\partial^2 f}{\partial x^2} = \sum_{i = 1}^n (-1)^{i + 1}c_i\frac{f(x + i \Delta x) - 2 f(x) + f(x - i \Delta x)}{i^2 \Delta x^2} + O(\Delta x^{2n}) \tag{25}
∂x2∂2f=i=1∑n(−1)i+1cii2Δx2f(x+iΔx)−2f(x)+f(x−iΔx)+O(Δx2n)(25)
其中:
- 系数 c 1 , … , c n c_1, \dots, c_n c1,…,cn 没有给出理论值. 在实际工作中, 由于 Δ x \Delta x Δx 比较大, 所以要专门计算系数, 它们与差分格式有关. 也是这个方向的重要研究内容. 表 1 给出了中间差分格式的系数.
- 误差为 O ( Δ x 2 n ) O(\Delta x^{2n}) O(Δx2n), 即 n n n 越大误差越小, 计算量也越大 (不知道是否可以用 GPU 计算, 速度就会增快很多).
- n n n 越大就涉及更远的点, 如果实际应用中的数据并没有对应那么高阶可导的函数, 效果不一定有那么好. 不过越远的点所对应的系数越小, 影响也没那么大.

2. 波动方程
2.1 弦振动 (横波) 方程
参见全波形反演的深度学习方法: 第 2 章 正演, 根据牛顿第二定律
F
=
m
a
(26)
F = ma \tag{26}
F=ma(26)
弦振动方程为
∂
2
u
(
x
,
t
)
∂
t
2
=
c
2
∂
2
u
(
x
,
t
)
∂
x
2
+
f
(
x
,
t
)
(27)
\frac{\partial^2 u(x, t)}{\partial t^2} = c^2 \frac{\partial^2 u(x, t)}{\partial x^2} + f(x, t) \tag{27}
∂t2∂2u(x,t)=c2∂x2∂2u(x,t)+f(x,t)(27)
其中
c
2
=
T
/
ρ
c^2 = T / \rho
c2=T/ρ,
f
(
x
,
t
)
=
F
(
x
,
t
)
/
ρ
f(x, t) = F(x, t) / \rho
f(x,t)=F(x,t)/ρ, 左式的物理意义是瞬时加速度
a
a
a, 右式第一项的物理意义是 单位质量所受的力
F
F
F,
c
c
c 的物理意义是速度.
进一步忽略重力
F
(
x
,
t
)
F(x, t)
F(x,t) 的作用, 可以推出一维齐次波动方程的解:
∂
2
u
(
x
,
t
)
∂
x
2
=
1
c
2
∂
2
u
(
x
,
t
)
∂
t
2
(28)
\frac{\partial^2 u(x, t)}{\partial x^2} = \frac{1}{c^2} \frac{\partial^2 u(x, t)}{\partial t^2} \tag{28}
∂x2∂2u(x,t)=c21∂t2∂2u(x,t)(28)
2.2 声波 (纵波) 方程
声波仅有纵波. 考虑二维的情况, 它满足
1
v
2
∂
2
U
∂
t
2
=
∂
2
U
∂
x
2
+
∂
2
U
∂
z
2
(29)
\frac{1}{v^2} \frac{\partial^2 U}{\partial t^2} = \frac{\partial^2 U}{\partial x^2} + \frac{\partial^2 U}{\partial z^2} \tag{29}
v21∂t2∂2U=∂x2∂2U+∂z2∂2U(29)
其中
U
U
U 指压力. 注意该式是物理定律, 不是从其它式子推导过来的.
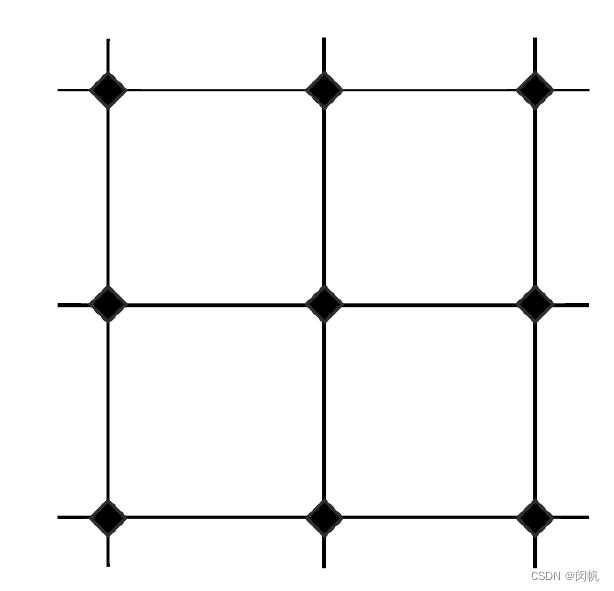
为了便于数值模拟, 将平面进行离散化, 仅考虑某些网格交叉点, 质量、压力等仅存在于这些点 (称为质点, 不知是否专业). 这样, 我们只考察第
i
i
i 行第
j
j
j 列的质点在时间
k
k
k 的压力
U
i
,
j
k
(30)
U_{i, j}^k \tag{30}
Ui,jk(30)
对于 2 阶精度, 将 (18) 式按照变量名改造后代入 (28) 式可得
1
v
2
U
i
,
j
k
+
1
−
2
U
i
,
j
k
+
U
i
,
j
k
−
1
Δ
t
2
=
U
i
+
1
,
j
k
−
2
U
i
,
j
k
+
U
i
−
1
,
j
k
Δ
x
2
+
U
i
,
j
+
1
k
−
2
U
i
,
j
k
+
U
i
,
j
−
1
k
Δ
y
2
(31)
\frac{1}{v^2} \frac{U_{i, j}^{k + 1} - 2 U_{i, j}^{k} + U_{i, j}^{k - 1}}{\Delta t^2} = \frac{U_{i + 1, j}^k - 2 U_{i, j}^{k} + U_{i - 1, j}^k}{\Delta x^2} + \frac{U_{i, j + 1}^k - 2 U_{i, j}^{k} + U_{i, j - 1}^k}{\Delta y^2} \tag{31}
v21Δt2Ui,jk+1−2Ui,jk+Ui,jk−1=Δx2Ui+1,jk−2Ui,jk+Ui−1,jk+Δy2Ui,j+1k−2Ui,jk+Ui,j−1k(31)
其中
k
+
1
k + 1
k+1 表示下一个时间点,
i
+
1
i + 1
i+1 表示下一个质点.
对于 4 阶精度, 将 (24) 式按照变量名改造后代入 (28) 式可得
1
v
2
U
i
,
j
k
+
1
−
2
U
i
,
j
k
+
U
i
,
j
k
−
1
Δ
t
2
=
c
1
U
i
+
1
,
j
k
−
2
U
i
,
j
k
+
U
i
−
1
,
j
k
Δ
x
2
+
c
1
U
i
,
j
+
1
k
−
2
U
i
,
j
k
+
U
i
,
j
−
1
k
Δ
y
2
+
c
2
U
i
+
2
,
j
k
−
2
U
i
,
j
k
+
U
i
−
2
,
j
k
Δ
x
2
+
c
2
U
i
,
j
+
2
k
−
2
U
i
,
j
k
+
U
i
,
j
−
2
k
Δ
y
2
+
O
(
Δ
x
4
)
(32)
\begin{array}{ll}\frac{1}{v^2} \frac{U_{i, j}^{k + 1} - 2 U_{i, j}^{k} + U_{i, j}^{k - 1}}{\Delta t^2} = &c_1 \frac{U_{i + 1, j}^k - 2 U_{i, j}^{k} + U_{i - 1, j}^k}{\Delta x^2} + c_1 \frac{U_{i, j + 1}^k - 2 U_{i, j}^{k} + U_{i, j - 1}^k}{\Delta y^2}\\ & + c_2 \frac{U_{i + 2, j}^k - 2 U_{i, j}^{k} + U_{i - 2, j}^k}{\Delta x^2} + c_2 \frac{U_{i, j + 2}^k - 2 U_{i, j}^{k} + U_{i, j - 2}^k}{\Delta y^2}\\ & + O(\Delta x^4) \end{array} \tag{32}
v21Δt2Ui,jk+1−2Ui,jk+Ui,jk−1=c1Δx2Ui+1,jk−2Ui,jk+Ui−1,jk+c1Δy2Ui,j+1k−2Ui,jk+Ui,j−1k+c2Δx2Ui+2,jk−2Ui,jk+Ui−2,jk+c2Δy2Ui,j+2k−2Ui,jk+Ui,j−2k+O(Δx4)(32)
继续推广可获得
2
n
2n
2n 阶精度的方程
1
v
2
U
i
,
j
k
+
1
−
2
U
i
,
j
k
+
U
i
,
j
k
−
1
Δ
t
2
=
∑
m
=
1
n
(
c
m
U
i
+
m
,
j
k
−
2
U
i
,
j
k
+
U
i
−
m
,
j
k
Δ
x
2
+
c
m
U
i
,
j
+
m
k
−
2
U
i
,
j
k
+
U
i
,
j
−
m
k
Δ
y
2
)
+
O
(
Δ
x
2
n
)
(32)
\frac{1}{v^2} \frac{U_{i, j}^{k + 1} - 2 U_{i, j}^{k} + U_{i, j}^{k - 1}}{\Delta t^2} = \sum_{m = 1}^n \left(c_m \frac{U_{i + m, j}^k - 2 U_{i, j}^{k} + U_{i - m, j}^k}{\Delta x^2} + c_m \frac{U_{i, j + m}^k - 2 U_{i, j}^{k} + U_{i, j - m}^k}{\Delta y^2}\right) + O(\Delta x^{2n})\tag{32}
v21Δt2Ui,jk+1−2Ui,jk+Ui,jk−1=m=1∑n(cmΔx2Ui+m,jk−2Ui,jk+Ui−m,jk+cmΔy2Ui,j+mk−2Ui,jk+Ui,j−mk)+O(Δx2n)(32)
利用式 (31) - (33), 根据 k k k 与 k − 1 k - 1 k−1 时刻各网格点的声压, 可以计算出 k + 1 k + 1 k+1 时刻各网格点的声压. 这样我们就可以正演啦.
3. 代码与结果
3.1 雷克子波
振源需要产生一个波, 它持续一小段时间.
tic
clc
close all
clear all
end_time = 0.5; % Total simulation time, in seconds
delta_t = 0.0005; % Time step, in seconds
f0 = 30; % The wave frequency, in 10~40 Hz
ricker_wave = zeros(end_time / delta_t + 1);
i = 1;
for time = 0: delta_t: end_time
ricker_wave(i) = 5.76 * f0^2 * (1 - 16 * (0.6 * f0 * time - 1)^2) * exp(-8 * (0.6 * f0 * time-1)^2);
i = i + 1;
end
plot(ricker_wave);

根据代码生成的子波如图 1 所示. 用它可以模拟振源仅波动一次的情况, 从开始小的振幅, 到最大振幅, 又来一个小振幅, 就形成了一个完整的波. 当 time 比较大的时候, 波动几乎为 0.
3.2 声波 2 阶精度
根据 (31) 式可以写出第一个声波方程所对应的模拟过程.
% acousti_wave.m
% Forward simulation of acoustic wave.
tic
clc
close all
clear all
end_time = 0.5; % Total simulation time, in seconds
delta_t = 0.0005; % Time step, in seconds
delta_x = 6; % Space step in the X direction, in meters
delta_z = 6; % Space step in the Z direction, in meters
cnx = 301; % Number of grids in X direction
cnz = 301; % Number of grids in Z direction
v = 1500; % The velocity of the wave, in meters/second
sx = (cnx + 1)/2; % The X position of the wave source
sz = (cnz + 1)/2; % The Z position of the wave source
f0 = 30; % The wave frequency, in 10~40 Hz
% Initialization
u_now = zeros(cnx, cnz); % The pressure at the current moment, it is a matrix for all points
u_prev = zeros(cnx, cnz); % The pressure at the previous moment
u_next = zeros(cnx, cnz); % The pressure at the next moment
% Simulate
for time = 0: delta_t: end_time
for i = 3: cnx - 2
for j = 3: cnz - 2
% Implement Eq. (31)
part1 = (-2 * u_now(i, j) + u_now(i + 1, j) + u_now(i - 1, j)) / delta_x^2;
part2 = (-2 * u_now(i, j) + u_now(i, j + 1) + u_now(i, j - 1)) / delta_z^2;
u_next(i, j) = 2 * u_now(i, j) - u_prev(i, j) + v^2 * (part1 + part2) * delta_t^2;
end
end
% The wave at the source
u_next(sx, sz) = 5.76 * f0^2 * (1 - 16 * (0.6 * f0 * time - 1)^2) * exp(-8 * (0.6 * f0 * time-1)^2);
% Update all points
u_prev = u_now;
u_now = u_next;
end
% Paint
surf(u_now)
shading interp;
view(2); %view(90,90)
colormap(gray);
toc

图 2 给出了 0.5 秒时的波场快照. 和池塘里丢一颗石头相似, 振源来自于 (151, 151), 因此 0.5 秒时波传播到外面 黑、白、黑三个圈依次对应于图 1 的振幅负、正、负.
3.3 声波 4 阶精度时的频散
修改步长、网格点参数.
% acousti_wave.m
% Forward simulation of acoustic wave.
tic
clc
close all
clear all
end_time = 0.5; % Total simulation time, in seconds
delta_t = 0.0005; % Time step, in seconds
delta_x = 12; % Space step in the X direction, in meters
delta_z = 12; % Space step in the Z direction, in meters
cnx = 151; % Number of grids in X direction
cnz = 151; % Number of grids in Z direction
v = 1500; % The velocity of the wave, in meters/second
sx = (cnx + 1)/2; % The X position of the wave source
sz = (cnz + 1)/2; % The Z position of the wave source
f0 = 30; % The wave frequency, in 10~40 Hz
c_1 = 9/8; % 16/15, 1
c_2 = -1/24; % -1/15, 0
% Initialization
u_now = zeros(cnx, cnz); % The pressure at the current moment, it is a matrix for all points
u_prev = zeros(cnx, cnz); % The pressure at the previous moment
u_next = zeros(cnx, cnz); % The pressure at the next moment
position_x = 70;
position_z = 70;
temp_wave = zeros(end_time / delta_t + 1);
k = 1;
% Simulate
for time = 0: delta_t: end_time
for i = 3: cnx - 2
for j = 3: cnz - 2
% Implement Eq. (31)
part1_1 = (-2 * u_now(i, j) + u_now(i + 1, j) + u_now(i - 1, j)) / delta_x^2;
part1_2 = (-2 * u_now(i, j) + u_now(i, j + 1) + u_now(i, j - 1)) / delta_z^2;
part2_1 = (-2 * u_now(i, j) + u_now(i + 2, j) + u_now(i - 2, j)) / delta_x^2;
part2_2 = (-2 * u_now(i, j) + u_now(i, j + 2) + u_now(i, j - 2)) / delta_z^2;
parts = c_1 * (part1_1 + part1_2) + c_2 * (part2_1 + part2_2);
u_next(i, j) = 2 * u_now(i, j) - u_prev(i, j) + v^2 * parts * delta_t^2;
end
end
% The wave at the source
u_next(sx, sz) = 5.76 * f0^2 * (1 - 16 * (0.6 * f0 * time - 1)^2) * exp(-8 * (0.6 * f0 * time-1)^2);
% Update all points
u_prev = u_now;
u_now = u_next;
temp_wave(k) = u_next(position_x, position_z);
k = k + 1;
end
plot(temp_wave);
toc



比较图 3至图 5 可以发现, 使用更好的系数, 可以一定程度压制多余的子波, 即频散. 但要接近图 1 (振源) 的效果, 还需要其它的方法.
3.4 运用于一般的波场数据
图 2 这种波场快照仅仅是一个圆圈. 对于实际的数据, 不同点的速度是不一样的, 代码会复杂很多吧?
No no no !!!
只需要把前面代码里的代码 v 替换成一个二维数组
v = zeros(cnx, cnz);
然后从数据文件里面将它读入. 其它的代码不需要改, (29) 式的声波方程已经把所有东西都考虑了.
有没有再次被物理雷到?
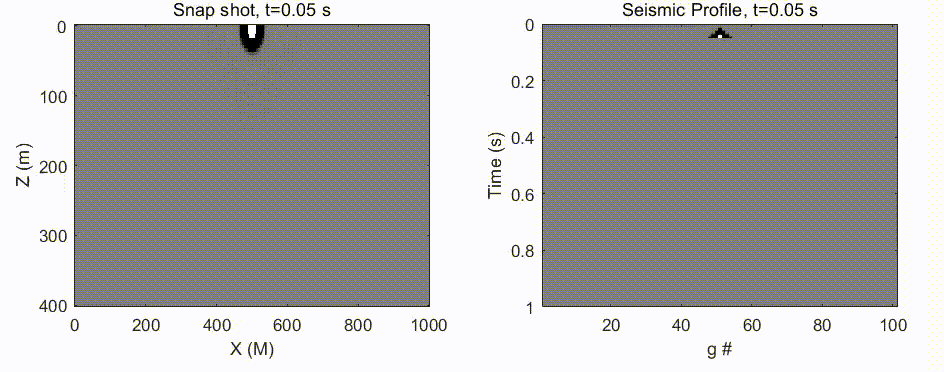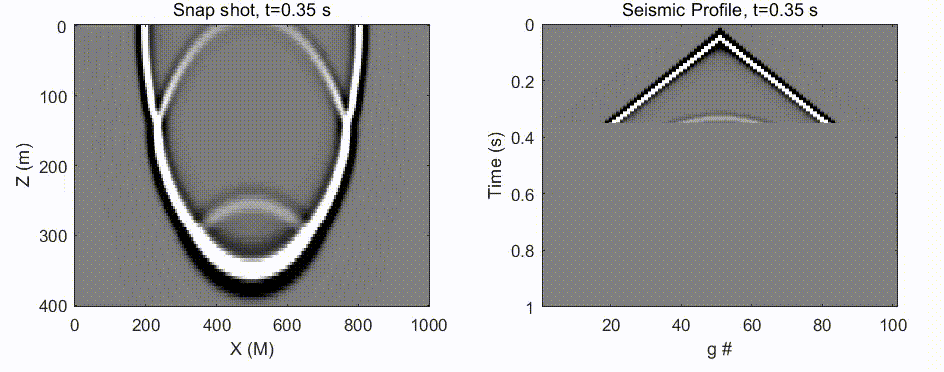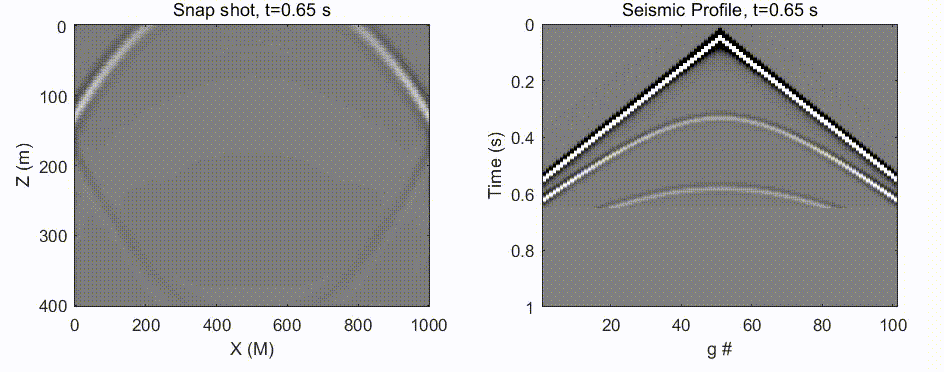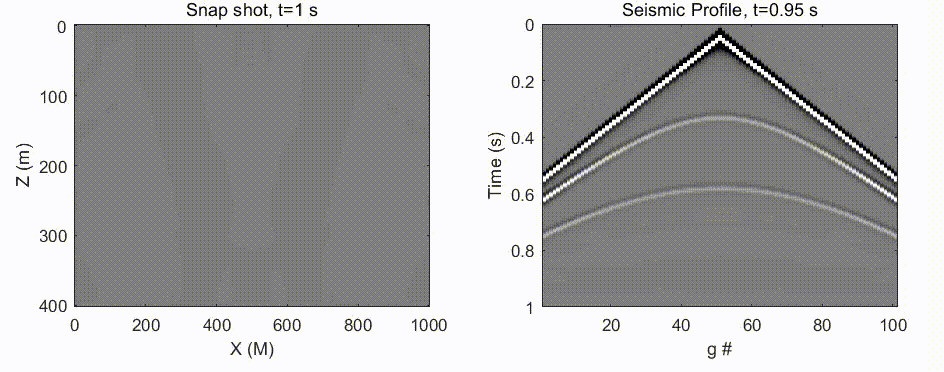
图 6 由张星移同学给出. 振源来自于中间顶部, 这符合我们在地球表面放炮的设定. 如左图所示, 波场快照开始的时候是一个半圆, 然后到深度 200 左右的时候遇到地层速度变化 (可能从泥土层到达花岗石层), 出现在反射、干涉等. 右图则记录了检波器 (均匀布置在地面上) 所获得的时序信号.
4. 小结
正演模拟看起来高大上, 但入门也没那么困难. 当然, 你要做深入了, 还是高大上!