计算机组成原理复习重点笔记
第三篇 中央处理器
- 第6章 计算机的运算方法
- 第7章 指令系统
- 第8章 CPU的结构和功能
第6章 计算机的运算方法
6.1 无符号数和有符号数
6.2 数的定点表示和浮点表示
6.3 定点运算
6.4 浮点四则运算
6.5 算术逻辑单元
6.1 定点数的表示
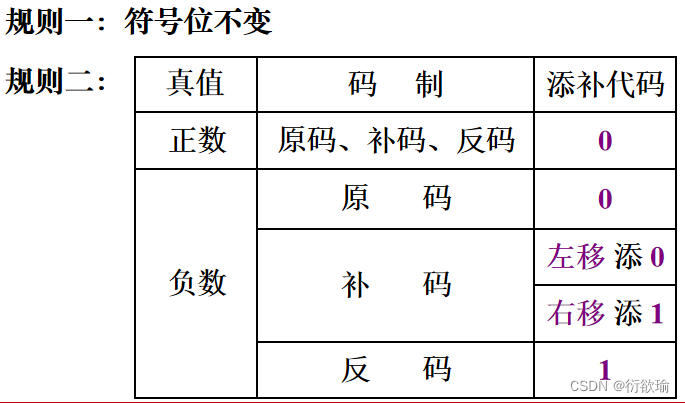
- 真值:正负号加绝对值表示的数值,如5,-3等。
- 机器数:计算机内部使用的,连同数符一起数码化了的数。
- 计算机常用的数值数据表示格式有两种:
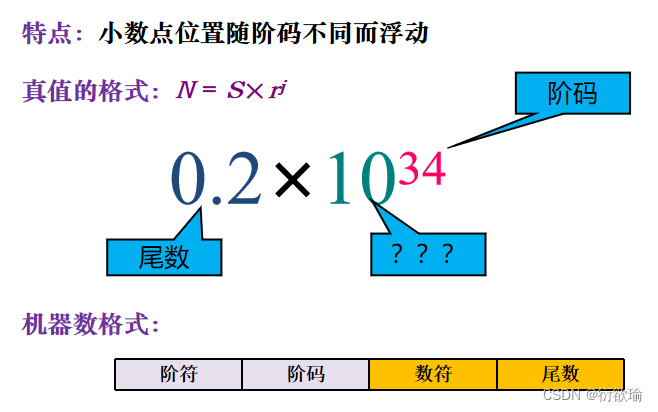
定点表示:小数点位置固定
浮点表示:小数点位置不固定 - 定点表示法
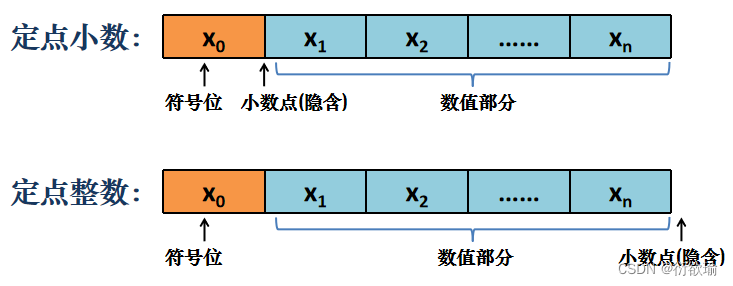
所有数据的小数点位置固定不变
小数点不用“.”表示,而是约定它的位置
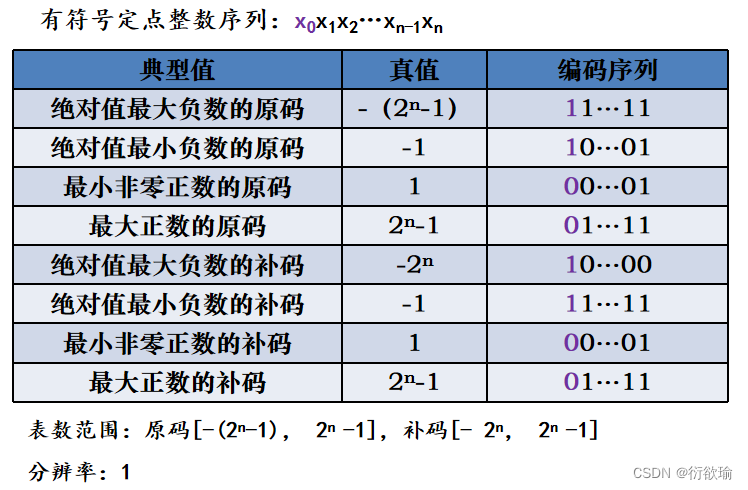
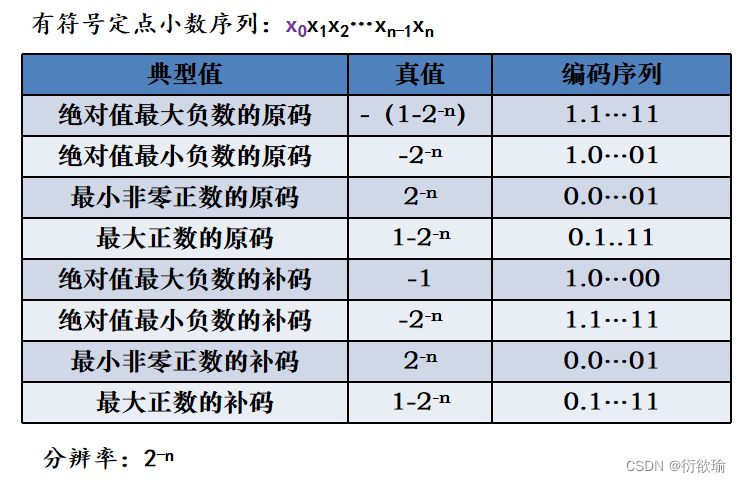
纯小数:小数点的位置在符号位之后最高有效位之前
纯整数:小数点位置在最低位之后
一、无符号数

二、有符号数
-
原码表示法


-
补码表示法
(1) 补的概念
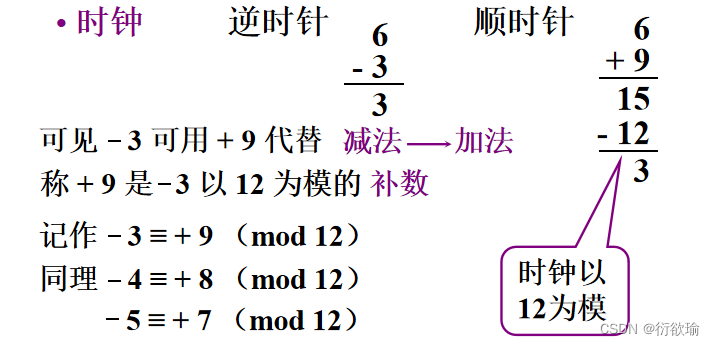
- 一个负数可用它的正补数来代替
- 正补数可以由模加上负数本身得到
- 一个正数和一个负数互为补数时,它们绝对值之和即为模数
- 正数的补码就是正数本身
- 计算机运算受字长限制,属于有模运算.

(2) 补码定义
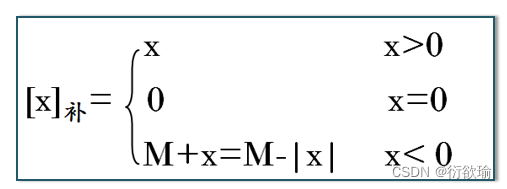
(3) 求补码的快捷方式(方法一)

(3) 求补码的快捷方式(方法二)

- 反码表示法

- 移码表示法

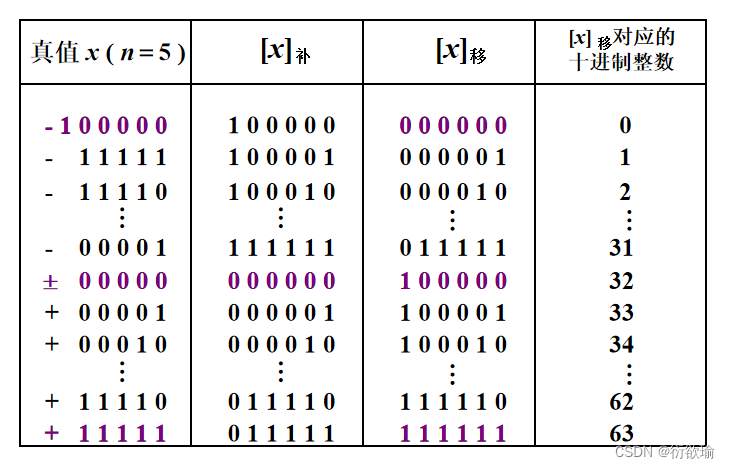
补码与移码只差一个符号位。
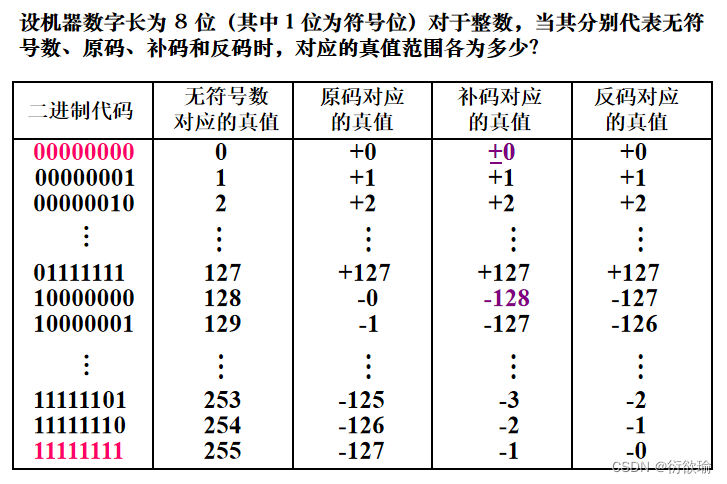
(3) 真值、补码和移码的对照表
6.2 数的浮点表示
2. 浮点数的表示范围(了解)
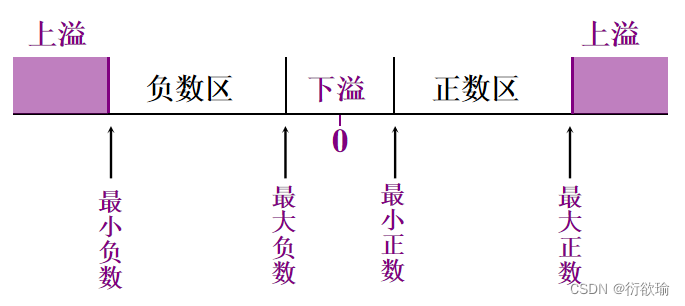
3. 浮点数据表示——IEEE754标准
- 1985年,IEEE(Institute of Electrical and Electronics Engineers,美国电气和电子工程师协会)提出了IEEE-754标准,目前几乎所有的计算机都支持该标准,从而方便了程序的移植。
- 标准规定了单精度(32)和双精度(64)的基本格式.
- 标准规定,尾数用原码,指数用移码(便于对阶和比较)
- 尾数域最左位(最高有效位)总是1, 故这一位经常不予存储,而认为隐藏在小数点的左边。
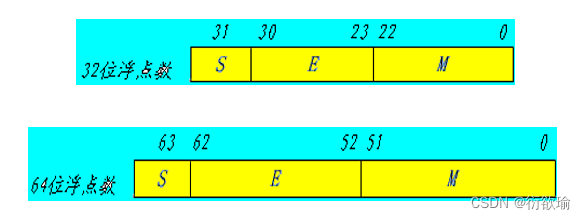
① - 基数R=2,基数固定,采用隐含方式来表示它。
- S:数的符号位,1位,在最高位。
- M:是尾数, 23位,在低位部分,采用纯小数表示
- E:是阶码,8位,采用移码表示。移码比较大小方便。
- 采用这种方式时,将浮点数的指数真值e变成阶码E时,应将指数e加上一个固定的偏移值127(01111111),即E=e+127。
- 一个规格化的32位浮点数x的真值表示为:
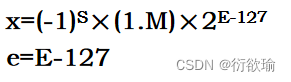
② - 基数R=2,基数固定,采用隐含方式来表示它。
- S:数的符号位,1位,在最高位。
- M:是尾数, 52位,在低位部分,采用纯小数表示
- E:是阶码,11位,采用移码表示。移码比较大小方便。
- 指数偏移值是1023。
- 因此规格化的64位浮点数x的真值为:
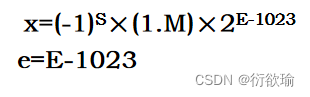
数据格式
- 当阶码E全0,尾数M全0时,表示真值0,结合符号位S为0或1,有正零和负零之分。
- 当阶码E全1,尾数M全0时,表示无穷大,结合符号位S为0或1,也有+∞和-∞之分。
- 这样在32位浮点数表示中,要除去E用全0和全1表示零和无穷大的特殊情况,指数的偏移值不选128(10000000),而选127(01111111)。对于规格化浮点数,E的范围变为1到254,真正的指数值e则为-126到+127。因此32位浮点数表示的绝对值的范围是10-38~1038。
6.3.1 移位运算
算术移位规则(P235)
带符号数的移位称为算术移位。
- 算术移位和逻辑移位的区别

6.3.2 加减法运算
- 补码加减运算公式(设机器字长为n+1)
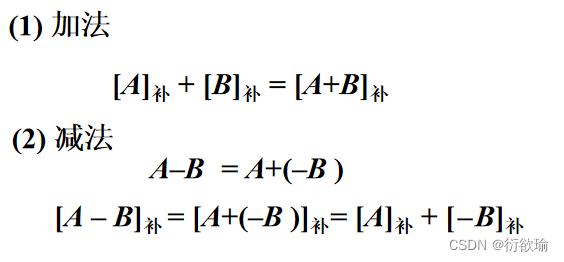
连同符号位一起相加,符号位产生的进位自然丢掉
- 溢出的检测


检测方法二:单符号位法
- 符号位的进位和最高数据位的进位相同,正确。
- 符号位的进位和最高数据位的进位不同,溢出。
6.3.3 乘法运算
- 分析笔算乘法

- 笔算乘法改进

- 改进后的笔算乘法过程(竖式)
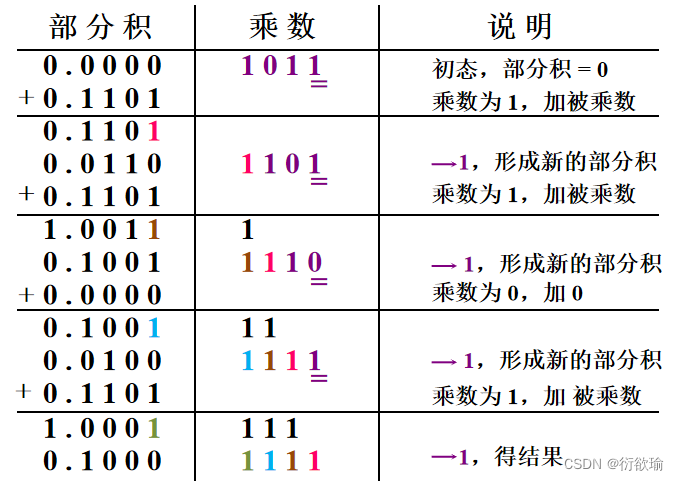
- 乘法 运算可用 加和移位实现
- n = 4,加 4 次,移 4 次
- 由乘数的末位决定被乘数是否与原部分积相加, 然后右移1 位形成新的部分积,同时 乘数右移1 位末位移丢,空出高位存放部分积的低位。
- 被乘数只与部分积的高位相加
- 原码乘法
(1) 原码一位乘运算规则

(2) 原码一位乘递推公式

原码一位乘法总结

5. 补码乘法
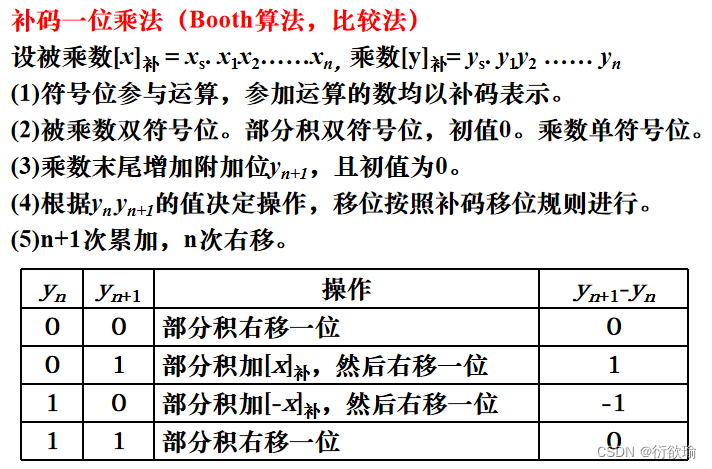
乘法小结
- 整数乘法与小数乘法完全相同,可用逗号代替小数点。
- 原码乘法,符号位单独处理,逻辑移位。
- 补码乘法,符号位参与运算、自然形成,补码右移。
- 不同的乘法运算需有不同的硬件支持。
6.3.4 除法运算
- 分析笔算除法

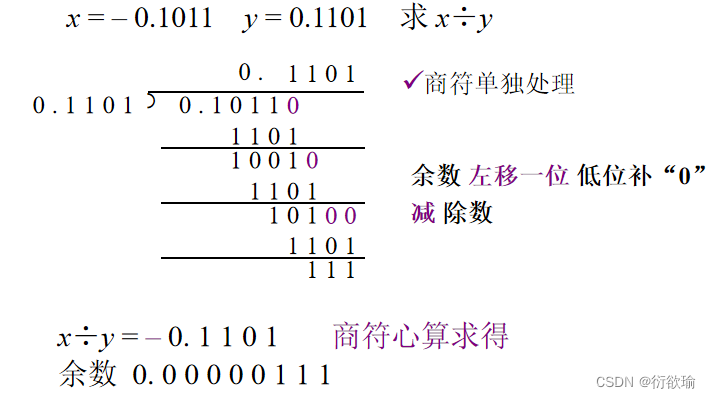
- 笔算除法和机器除法的比较

- 原码除法(不恢复余数法,也叫加减交替法)

- 补码除法(p264)

x 与 y 异号

② 商值的确定——末位恒置“1”法
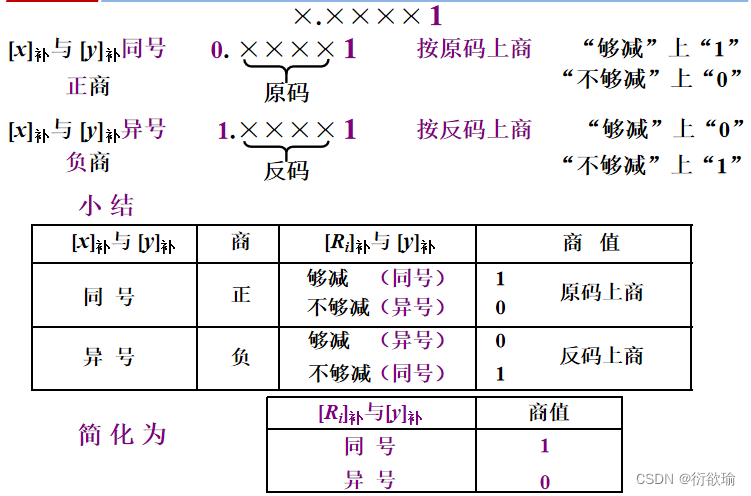 (2) 商符的形成
(2) 商符的形成

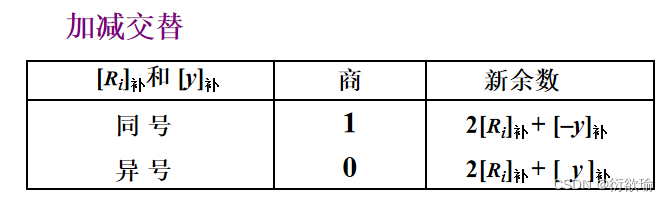
(3) 新余数的获得
- 补码除法(p264)
补码除法(加减交替法)
1.符号位与数值位一起参加运算,商符自然形成。
2.第一步,若X和Y同号,算X-Y;若X和Y异号,算X+Y。
3.若余数R与Y同号,上商1,2[Ri]补 + [–y]补。
若余数R与Y异号,上商0 ,2[Ri]补 + [y]补。
4.重复执行第3步n次。
5.一般采用末尾置1法。
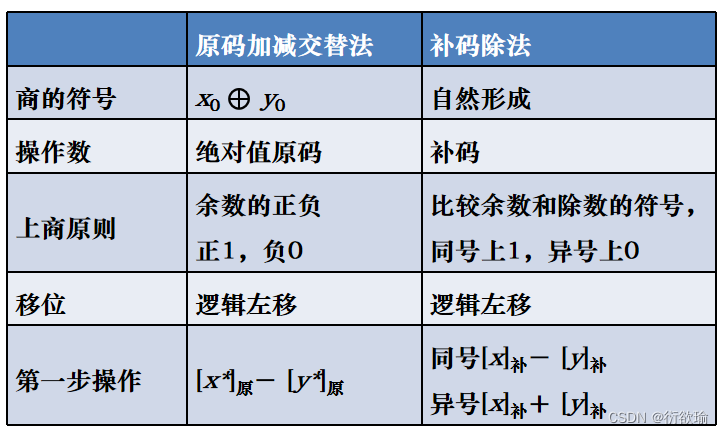
(5) 补码除和原码除(加减交替法)比较
6.4 浮点四则运算
一、浮点加减运算

2. 尾数求和
- 规格化


4. 舍入


6.5 算术逻辑单元(了解)
- 一位全加器
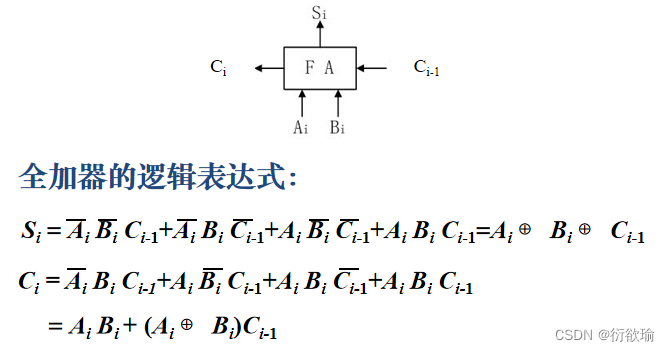
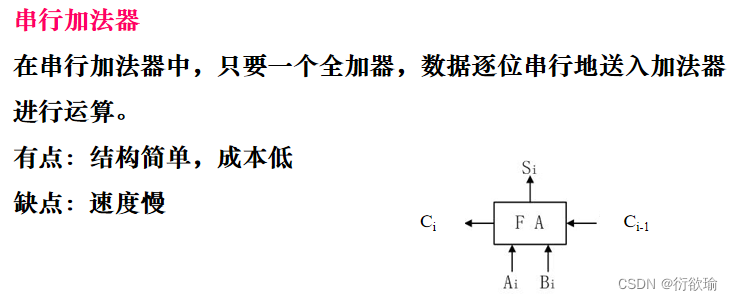
- 并行加法器
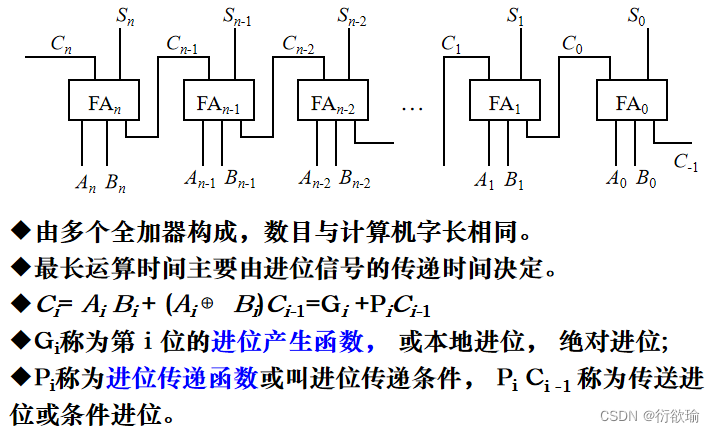

- 串行进位链
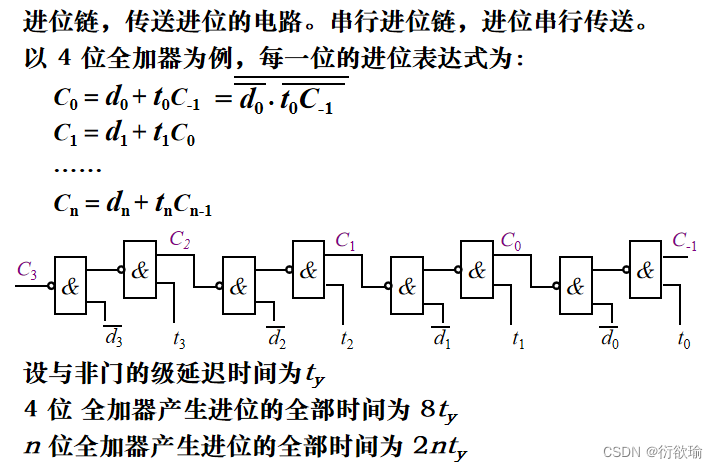
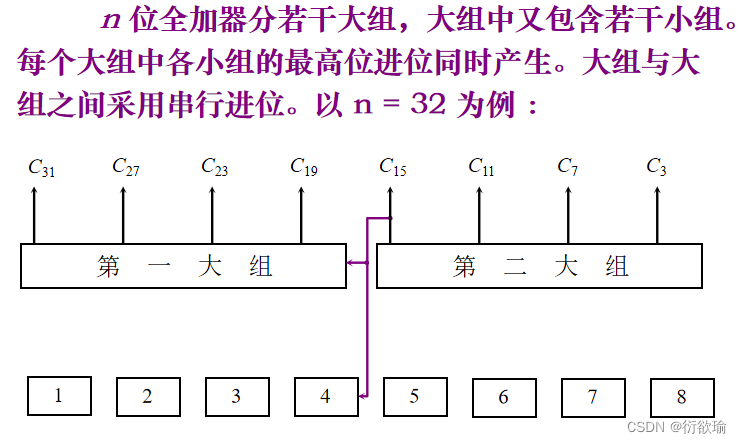
- 并行进位链(先行进位,跳跃进位)
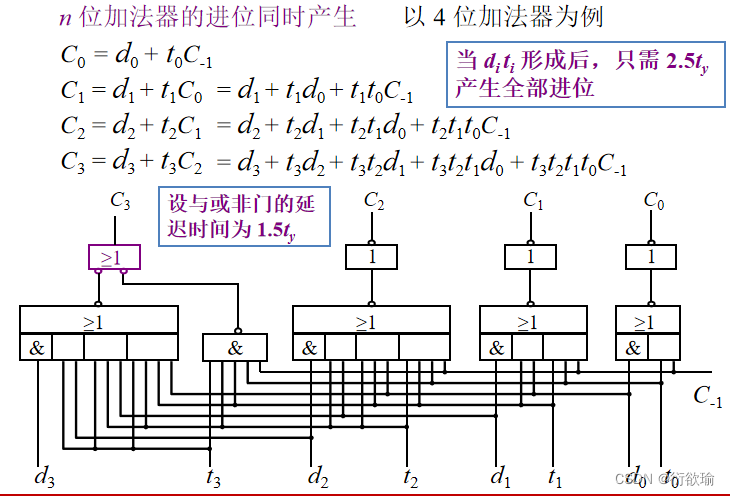
(1) 单重分组跳跃进位链
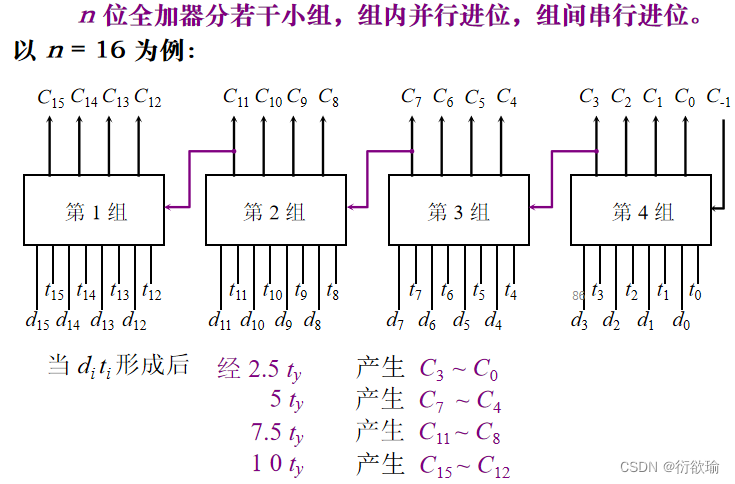
(2) 双重分组跳跃进位链

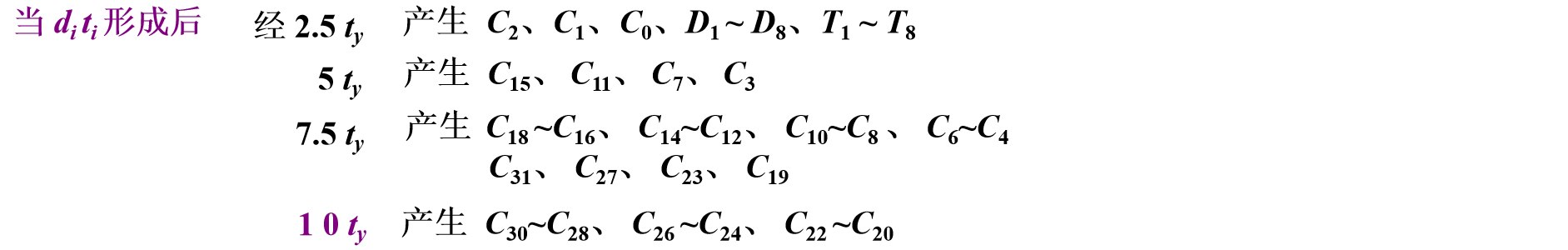
编辑于2022/12/15日;
距离考试还有一周+不满一天。


![【简单项目实战】用C++实现学生成绩管理系统 | [面向对象]](https://img-blog.csdnimg.cn/698820809eb842a5bbf531258e2713e7.png)