查找算法在我们的面试和开发中,是很常见的一种算法,今天我就给大家介绍几个常用的查找算法。
一. 线性查找
1.概念
线性查找也叫顺序查找,这是最基本的一种查找方法。该算法是从给定的值中进行搜索,从一端开始逐一检查每个元素,直到找到所需的元素为止。在线下查找中,元素序列的排列可以有序,也可以无序。
2.代码实现
public class Test01 {
public static void main(String[] args) {
//线性查找
int[] arr = {45, 62, 15,62, 78, 30};
int index = sequentialSearch01(arr, 62);
System.out.println("指定元素首次出现的下标位置:" + index);
List<Integer> indexList = sequentialSearch02(arr, 62);
System.out.println("指定元素出现的下标位置的集合:" + Arrays.toString(indexList.toArray()));
}
/**
* 顺序查找
* 返回指定元素首次出现的下标位置
*/
public static int sequentialSearch01(int[] arr,int value){
for (int i = 0; i < arr.length; i++) {
if(arr[i] == value){
return i;
}
}
return -1;
}
/**
* 顺序查找
* 返回指定元素出现的下标位置的集合
*/
public static List<Integer> sequentialSearch02(int[] arr,int value){
List<Integer> list = new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
if(arr[i] == value){
list.adds(i);
}
}
return list;
}
}二. 二分法查找
1.概念
二分查找(Binary Search)算法,也叫折半查找算法。当要从一个序列中查找一个元素的时候,二分查找是一种非常快速的查找算法。二分查找是针对有序数据集合的查找算法,如果是无序数据集合就遍历查找。
二分查找之所以快速,是因为它在匹配不成功的时候,每次都能排除剩余元素中一半的元素。因此可能包含目标元素的有效范围就收缩得很快,而不像顺序查找那样,每次仅能排除一个元素。
2.原理
比如有一个有序表数组[1,3,5,7,9,11,13,15,17,19,21],它是按照从小到大的顺序来进行排列的,现在需要在该有序表中查找元素19,步骤如下:
1.首先设置两个指针low和high,分别指向数据集合的第一个数据元素1(位序为0)和最后一个数据元素21(位序为10)。
2.然后把整个数据集合长度分成两半,并用一个指针指向它们的临界点,所以定义指针mid指向了中间元素11(位序5),也就是说mid=(high+low)/2,其中high和low都代表所指向的元素的位序,如下图:
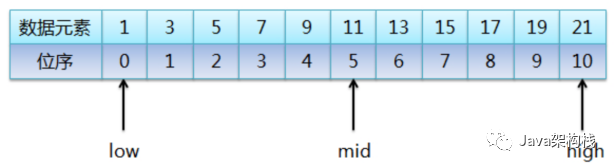
3.接着,将mid所指向的元素(11)与待查找元素(19)进行比较。因为19大于11,说明待查找的元素(19)一定位于mid和high之间。所以继续折半,则low = mid+1,而mid = (low+high)/2,结果如下图:
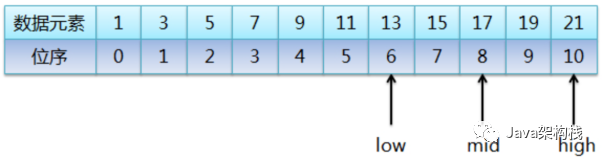
4.接着,又将mid所指向的元素(17)与待查找元素(19)进行比较,由于19大于17,所以继续折半,则low = mid+1,而mid = (low+high)/2,结果如下图:
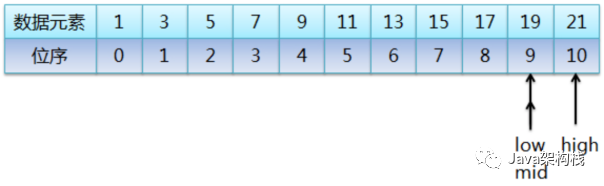
5.最后,又将mid所指向的元素(19)与待查找元素(19)进行比较,结果相等,则查找成功,返回mid指针指向的元素的位序。
如果查找的元素值不是19,而是20,那么在最后一步之前还得继续折半查找,最后出现的情况如下图:

3.代码实现
public class Test01 {
public static void main(String[] args) {
//二分法查找
int[] arr = {1,2,3,4,5,6,7,8,9,11,11,11,11,11,11};
int index = binarySearch01(arr, 11);
System.out.println("指定元素出现的下标位置:" + index);
List<Integer> indexList = binarySearch02(arr, 11);
System.out.println("指定元素出现的下标位置的集合:" + Arrays.toString(indexList.toArray()));
index = recursionbinarySearch01(arr, 0, arr.length-1, 11);
System.out.println("递归方式 - 指定元素出现的下标位置:" + index);
indexList = recursionbinarySearch02(arr, 0, arr.length-1, 11);
System.out.println("递归方式 - 指定元素出现的下标位置的集合:" + Arrays.toString(indexList.toArray()));
}
/**
* 有序的数组中查找某个元素出现的下标位置
* 不使用递归的二分查找
* 返回出现的下标位置
*/
public static int binarySearch01(int[] arr,int val){
int low = 0;
int high = arr.length-1;
while(low <= high){
int mid = (low + high)/2;
if(val > arr[mid]){
//目标在右侧
low = mid+1;
}else if(val < arr[mid]){
//目标在左侧
high = mid-1;
}else{
return mid;
}
}
return -1;
}
/**
* 有序的数组中查找某个元素首次出现的下标位置
* 不使用递归的二分查找
* 返回下标集合
*/
public static List<Integer> binarySearch02(int[] arr,int val){
int low = 0;
int high = arr.length-1;
while(low <= high){
int mid = (low + high)/2;
if(val > arr[mid]){
//目标在右侧
low = mid+1;
}else if(val < arr[mid]){
//目标在左侧
high = mid-1;
}else{
// 定义放置索引下标的集合
List<Integer> list = new ArrayList<>();
// 将首次查找的位置放入集合
list.add(mid);
// 判断是否还有重复值
int index = mid + 1;
while(index < arr.length){
if(arr[index] == val){
list.add(index);
}else{
break;
}
index++;
}
index = mid-1;
while(index >= 0){
if(arr[index] == val){
list.add(index);
}else{
break;
}
index--;
}
return list;
}
}
return null;
}
/**
* 有序的数组中查找某个元素出现的下标位置
* 使用递归的二分查找
* 返回出现的下标位置
*/
public static int recursionbinarySearch01(int[] arr,int low,int high,int val){
if(val < arr[low] || val > arr[high] || low > high){
return -1;
}
int mid = (low + high)/2;
if(val > arr[mid]){
//目标在右侧
return recursionbinarySearch01(arr, mid+1, high, val);
}else if(val < arr[mid]){
//目标在左侧
return recursionbinarySearch01(arr, low, mid-1, val);
}else{
return mid;
}
}
/**
* 有序的数组中查找某个元素首次出现的下标位置
* 使用递归的二分查找
* 返回下标集合
*/
public static List<Integer> recursionbinarySearch02(int[] arr,int low,int high,int val){
if(val < arr[low] || val > arr[high] || low > high){
return null;
}
int mid = (low + high)/2;
if(val > arr[mid]){
//目标在右侧
return recursionbinarySearch02(arr, mid+1, high, val);
}else if(val < arr[mid]){
//目标在左侧
return recursionbinarySearch02(arr, low, mid-1, val);
}else{
// 定义放置索引下标的集合
List<Integer> list = new ArrayList<>();
// 将首次查找的位置放入集合
list.add(mid);
// 判断是否还有重复值
int index = mid + 1;
while(index < arr.length){
if(arr[index] == val){
list.add(index);
}else{
break;
}
index++;
}
index = mid-1;
while(index >= 0){
if(arr[index] == val){
list.add(index);
}else{
break;
}
index--;
}
return list;
}
}
}4.优缺点
优点:速度快,不占空间,不开辟新空间缺点:必须是有序的数组,数据量太小没有意义
三. 插值查找
1.概念
从折半查找中可以看出,折半查找的查找效率还是不错的。可是为什么要折半呢?为什么不是四分之一、八分之一呢?
举个例子,如果我们要在英语词典中查找“hello”这个单词,会首先翻开字典的中间部分,然后继续折半吗?肯定不会,对于查找单词“hello”,我们肯定是下意识的往字典的最前部分翻去,而查找单词“zero”则相反,我们会下意识的往字典的最后部分翻去。
所以在折半查找法的基础上进行改造就出现了插值查找法,也叫做按比例查找。所以插值查找与折半查找唯一不同的是在于mid的计算方式上,它的计算方式为:
int mid = low + (high - low) * (val- arr[low]) / (arr[high] - arr[low])
这样就能快速定位目标数值所在的索引,比二分查找可以更快速实现查找。
自适应获取mid,也就是自适应查找点。
2.代码实现
public class Test01 {
public static void main(String[] args) {
//插值查找
int[] arr = {1,2,3,4,5,6,7,8,9,11,11,11,11,11,11};
int index = insertSearch01(arr, 11);
System.out.println("指定元素出现的下标位置:" + index);
List<Integer> indexList = insertSearch02(arr, 11);
System.out.println("指定元素出现的下标位置的集合:" + Arrays.toString(indexList.toArray()));
index = recursionInsertSearch01(arr, 0, arr.length-1, 11);
System.out.println("递归方式 - 指定元素出现的下标位置:" + index);
indexList = recursionInsertSearch02(arr, 0, arr.length-1, 11);
System.out.println("递归方式 - 指定元素出现的下标位置的集合:" + Arrays.toString(indexList.toArray()));
}
/**
* 有序的数组中查找某个元素出现的下标位置
* 不使用递归的二分查找
* 返回出现的下标位置
*/
public static int insertSearch01(int[] arr,int val){
int low = 0;
int high = arr.length-1;
while(low <= high){
int mid = low + (high - low) * (val - arr[low])/(arr[high] - arr[low]);
if(val > arr[mid]){
//目标在右侧
low = mid+1;
}else if(val < arr[mid]){
//目标在左侧
high = mid-1;
}else{
return mid;
}
}
return -1;
}
/**
* 有序的数组中查找某个元素首次出现的下标位置
* 不使用递归的二分查找
* 返回下标集合
*/
public static List<Integer> insertSearch02(int[] arr,int val){
int low = 0;
int high = arr.length-1;
while(low <= high){
int mid = low + (high - low) * (val - arr[low])/(arr[high] - arr[low]);
if(val > arr[mid]){
//目标在右侧
low = mid+1;
}else if(val < arr[mid]){
//目标在左侧
high = mid-1;
}else{
// 定义放置索引下标的集合
List<Integer> list = new ArrayList<>();
// 将首次查找的位置放入集合
list.add(mid);
// 判断是否还有重复值
int index = mid + 1;
while(index < arr.length){
if(arr[index] == val){
list.add(index);
}else{
break;
}
index++;
}
index = mid-1;
while(index >= 0){
if(arr[index] == val){
list.add(index);
}else{
break;
}
index--;
}
return list;
}
}
return null;
}
/**
* 有序的数组中查找某个元素出现的下标位置
* 使用递归的二分查找
* 返回出现的下标位置
*/
public static int recursionInsertSearch01(int[] arr,int low,int high,int val){
if(val < arr[low] || val > arr[high] || low > high){
return -1;
}
int mid = low + (high - low) * (val - arr[low])/(arr[high] - arr[low]);
if(val > arr[mid]){
//目标在右侧
return recursionInsertSearch01(arr, mid+1, high, val);
}else if(val < arr[mid]){
//目标在左侧
return recursionInsertSearch01(arr, low, mid-1, val);
}else{
return mid;
}
}
/**
* 有序的数组中查找某个元素首次出现的下标位置
* 使用递归的二分查找
* 返回下标集合
*/
public static List<Integer> recursionInsertSearch02(int[] arr,int low,int high,int val){
if(val < arr[low] || val > arr[high] || low > high){
return null;
}
int mid = low + (high - low) * (val - arr[low])/(arr[high] - arr[low]);
if(val > arr[mid]){
//目标在右侧
return recursionInsertSearch02(arr, mid+1, high, val);
}else if(val < arr[mid]){
//目标在左侧
return recursionInsertSearch02(arr, low, mid-1, val);
}else{
// 定义放置索引下标的集合
List<Integer> list = new ArrayList<>();
// 将首次查找的位置放入集合
list.add(mid);
// 判断是否还有重复值
int index = mid + 1;
while(index < arr.length){
if(arr[index] == val){
list.add(index);
}else{
break;
}
index++;
}
index = mid-1;
while(index >= 0){
if(arr[index] == val){
list.add(index);
}else{
break;
}
index--;
}
return list;
}
}
}四. 斐波那契查找
1.概念
斐波那契查找也叫做黄金分割法查找,这种查找法其实也是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找,提高查找效率。同样地,斐波那契查找也属于一种有序查找算法。
2.原理
对于斐波那契数列:1、1、2、3、5、8、13、21、34、55、89……(也可以从0开始),前后两个数字的比值随着数列的增加,越来越接近黄金比值0.618。比如元素个数为89的有序列表,89在斐波那契数列中是34和55相加所得。
把元素个数为89的有序列表分成:前55个数据元素组成的前半段和34个数据元素组成的后半段。那么前半段元素个数和整个有序表长度的比值接近黄金比值0.618,而前后两段长度的比值也接近黄金比值0.618。
假如要查找的元素在前半段,那么继续按照斐波那契数列来看,55 = 34 + 21,所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段,继续查找,如此反复,直到查找成功或失败。这样斐波那契数列就被应用到查找算法中了。
总长度=f[k],前半段长度=f[k-1],后半段长度=f[k-2]
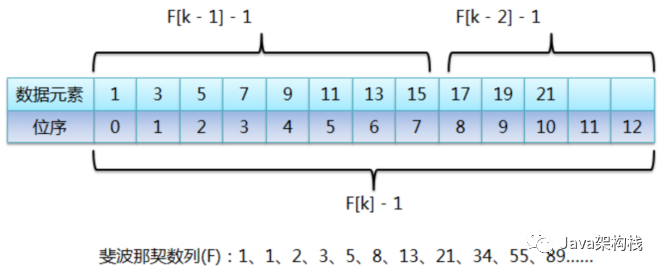
有序列表的元素个数不是斐波那契数列中的数字时该如何处理呢?
当有序表的元素个数不是斐波那契数列中的某个数字时,需要把有序列表的长度补齐,让它成为斐波那契数列中的一个数值。
如果不是补齐,而是将多余的截掉是否可行?把原有序列表截断肯定是不可行的,因为可能把要查找的目标值截掉。
每次取斐波那契数列中的某个值时(f[k]),都会进行-1操作,这是因为数组下标从0开始。
3.代码实现
public class Test01 {
public static void main(String[] args) {
int[] arr = {1,13,25,37,49,51,62,68,70,80,80};
List<Integer> fiboSearchList = fiboSearchList(arr, 80);
System.out.println(Arrays.toString(fiboSearchList.toArray()));
}
public static List<Integer> fiboSearchList(int[] arr, int val) {
int low = 0;
int high = arr.length-1;
// 斐波那契的索引下标。数组长度的数值在斐波那契数列中对应的索引下标
int[] fiboArray = getFiboArray(10);//[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
// 斐波那契的索引下标。数组长度的数值在斐波那契数列中对应的索引下标
int k = 0;
// 斐波那契的索引下标。数组长度的数值在斐波那契数列中对应的索引下标
while(arr.length > fiboArray[k]){
k++;
}
System.out.println("k = " + k);//6
System.out.println("fiboArray = " + Arrays.toString(fiboArray));//[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
// 利用Java工具类Arrays 构造新数组并指向 数组 arr[]
int[] temp = Arrays.copyOf(arr, fiboArray[k]);
System.out.println("temp=" + Arrays.toString(temp));
//[1, 13, 25, 37, 49, 51, 62, 68, 70, 80, 80, 0, 0]
//对新构造的数组进行元素补充,补充为最高位的数值
for (int i = high+1; i < temp.length; i++) {
temp[i] = arr[high];
}
System.out.println("补充数值的temp=" + Arrays.toString(temp));
//[1, 13, 25, 37, 49, 51, 62, 68, 70, 80, 80, 80, 80]
while(low <= high){
//数列左侧有f[k-1]个元素
int mid = low + fiboArray[k-1] - 1;
if(val < temp[mid]){
// 目标值小于mid所在元素,在左侧查找
high = mid-1;
/*全部元素=前部元素+后部元素
* f[k]=f[k-1]+f[k-2]
* 因为左侧有f[k-1]个元素,所以可以继续拆分f[k-1]=f[k-2]+f[k-3]
* 即在f[k-1]的前部继续查找 所以k-=1
* 即下次循环 mid=f[k-1-1]-1
*/
k-=1;
}else if(val > temp[mid]){
// 目标值大于mid所在元素,在右侧查找
low = mid+1;
/*全部元素=前部元素+后部元素
* f[k]=f[k-1]+f[k-2]
* 因为右侧有f[k-2]个元素,所以可以继续拆分f[k-2]=f[k-3]+f[k-4]
* 即在f[k-2]的前部继续查找 所以k-=2
* 即下次循环 mid=f[k-1-2]-1
*/
k -= 2;
}else{
// 定义放置索引下标的集合
ArrayList<Integer> list = new ArrayList<>();
list.add(mid);
int index = mid+1;
while(index < arr.length){
if(arr[index] == val){
list.add(index);
index++;
}else{
break;
}
}
index = mid-1;
while(index > 0){
if(arr[index] == val){
list.add(index);
index--;
}else{
break;
}
}
return list;
}
}
return null;
}
public static int[] getFiboArray(int maxSize){
int[] fiboArray = new int[maxSize];
fiboArray[0] = 1;
fiboArray[1] = 1;
for (int i = 2; i < fiboArray.length; i++) {
fiboArray[i] = fiboArray[i-1] + fiboArray[i-2];
}
return fiboArray;
}
}







![[力扣] 剑指 Offer 第二天 - 从尾到头打印链表](https://img-blog.csdnimg.cn/1352715ade8749edae88dc29d5c73125.png)