原题
给你一棵根为 root 的二叉树,请你返回二叉树中好节点的数目。
「好节点」X 定义为:从根到该节点 X 所经过的节点中,没有任何节点的值大于 X 的值。
示例 1:
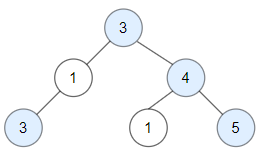
输入:root = [3,1,4,3,null,1,5] 输出:4 解释:图中蓝色节点为好节点。 根节点 (3) 永远是个好节点。 节点 4 -> (3,4) 是路径中的最大值。 节点 5 -> (3,4,5) 是路径中的最大值。 节点 3 -> (3,1,3) 是路径中的最大值。
示例 2:
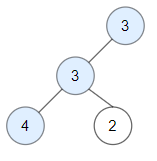
输入:root = [3,3,null,4,2] 输出:3 解释:节点 2 -> (3, 3, 2) 不是好节点,因为 "3" 比它大。
示例 3:
输入:root = [1] 输出:1 解释:根节点是好节点。
提示:
- 二叉树中节点数目范围是
[1, 10^5]。 - 每个节点权值的范围是
[-10^4, 10^4]。
解题思路
显然我们需要遍历每个节点,并且将当前路径上最大值一起往下传,是一个和路径深度有关系的问题,考虑使用DFS实现遍历:
class Solution {
public:
int goodNodes(TreeNode* root) {
return dfs(root);
}
void dfs(TreeNode* root) {
if(root == nullptr){
return;
}
visit(root);
dfs(root->left);
dfs(root->right);
}
};假设我们当前有一个节点root和路径上传下来的最大值path_max。如果当前节点值小于path_max,那我们继续把path_max传给它的左右节点。如果当前节点值大于path_max,则把path_max设为当前节点值,并且把path_max传给它的左右节点。而当前节点的好节点数,等于左右节点的号节点数之和,加上1,如果当前节点是好节点,否则不加。考虑到根节点一定是好节点,我们可以用INT_MIN作为path_max的初始值。于是我们得到完整的实现:
class Solution {
public:
int goodNodes(TreeNode* root) {
return dfs(root,INT_MIN);
}
void dfs(TreeNode* root, int path_max) {
if(root == nullptr){
return 0;
}
int res = 0;
if(root->val >= path_max){
res++;
path_max = root->val;
}
res += dfs(root->left, path_max);
res += dfs(root->right, path_max);
return res;
}
};