目录
1 矩阵
1.1 1维的矩阵
1.2 2维的矩阵
1.3 没有3维的矩阵---3维的是3阶张量
1.4 下面本文总结的都是各种特殊效果矩阵特例
2 方阵: 正方形矩阵
3 单位矩阵
3.1 单位矩阵的定义
3.2 单位矩阵的特性
3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]
3.4 零矩阵
3.4 看下这个矩阵 [0,1;1,0]
3.5 看下这个矩阵 [1,1;1,1]
4 镜像矩阵
5 旋转矩阵
5.1 定义
5.2 以下是选择矩阵的原理（转载）
5.3 旋转矩阵应用转移点： 旋转矩阵右乘其他矩阵才可以
6 伸缩矩阵
7 剪切矩阵
8 平移矩阵？？？
待补充：其他特殊矩阵
1 矩阵
1.1 1维的矩阵
- 行向量，αT
- 列向量，α
行向量
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
\end{matrix}
\right]
$$
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
\end{matrix}
\right]
$$
列向量
$$
\left[
\begin{matrix}
1 \\
4 \\
7
\end{matrix}
\right]
$$
1.2 2维的矩阵
- 一般2维表都可以看作矩阵。
- 矩阵的每个维度可以是1个数字，也可以是多个数字组成的数组/向量
- 比如 An*m就是n 行 m列的矩阵
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{matrix}
\right] \tag{1}
$$
1.3 没有3维的矩阵---3维的是3阶张量
- 比如3个坐标轴
1.4 下面本文总结的都是各种特殊效果矩阵特例
- 单位矩阵
- 零矩阵
- 等等
2 方阵: 正方形矩阵
- 行数和列数相等的矩阵即方阵
- 比如 An*n就是n 行 n列的矩阵
- 方阵有很多特殊的属性
- 比如虽然并不是，方阵一定有逆矩阵，但是可逆矩阵必须是方阵
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix}
\right]
$$
3 单位矩阵
3.1 单位矩阵的定义
- 单位矩阵，一定是这样的[1,0;0,1]
- 单位矩阵的作用，矩阵A*I=A
- 矩阵 [1,0;0,1] 代表将其他矩阵 原样进行映射，不做任何改变
- 也就是单位矩阵，既不改变矩阵方向，也不改变伸缩矩阵的长短，完全不变
$$
\left[
\begin{matrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}
\right]
$$
3.2 单位矩阵的特性
- 单位矩阵的特性
- A*I=A
- A*A-=I
3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]
- 因为 矩阵 [1,0;0,1] 代表将其他矩阵 原样进行映射，不做任何改变
- 而[1,1;1,1] 没有啥意义
- 可比较下面的结果，实际理解
3.4 零矩阵
- [0,0;0,0]
- 所有的列向量，都坍缩回原点
$$
\left[
\begin{matrix}
0 & 0 \\
0 & 0 \\
\end{matrix}
\right]
$$
3.4 看下这个矩阵 [0,1;1,0]
- [0,1;1,0]
- 这个矩阵，和单位矩阵形式恰好相反
- 从几何效果来看，是镜像矩阵（列向量互换了）
$$
\left[
\begin{matrix}
0 & 1 \\
1 & 0 \\
\end{matrix}
\right]
$$
3.5 看下这个矩阵 [1,1;1,1]
- [1,1;1,1]
- 几何效果是，矩阵的列向量会被变成完全相等（方向，长度都相等）
$$
\left[
\begin{matrix}
1 & 1 \\
1 & 1 \\
\end{matrix}
\right]
$$
4 镜像矩阵
- [0,1;1,0]
- 这个矩阵，和单位矩阵形式恰好相反
- 从几何效果来看，是镜像矩阵（列向量互换了）
$$
\left[
\begin{matrix}
0 & 1 \\
1 & 0 \\
\end{matrix}
\right]
$$
5 旋转矩阵
5.1 定义
- 经典的旋转矩阵及其变形
- cos(θ) -sin(θ)
sin(θ) cos(θ) - 可以实现，逆时针旋转效果
$$
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
$$
$$
\left[
\begin{matrix}
1 & 0 & 0 \\
0 & cos(θ) & -sin(θ) \\
0 & sin(θ) & cos(θ) \\
\end{matrix}
\right]
$$
5.2 以下是选择矩阵的原理（转载）
旋转变换（一）旋转矩阵_csxiaoshui的博客-CSDN博客本文主要介绍了计算机图形学中的旋转的概念和矩阵的描述方式，包括二维和三维旋转矩阵的推导过程_旋转矩阵https://blog.csdn.net/csxiaoshui/article/details/65446125
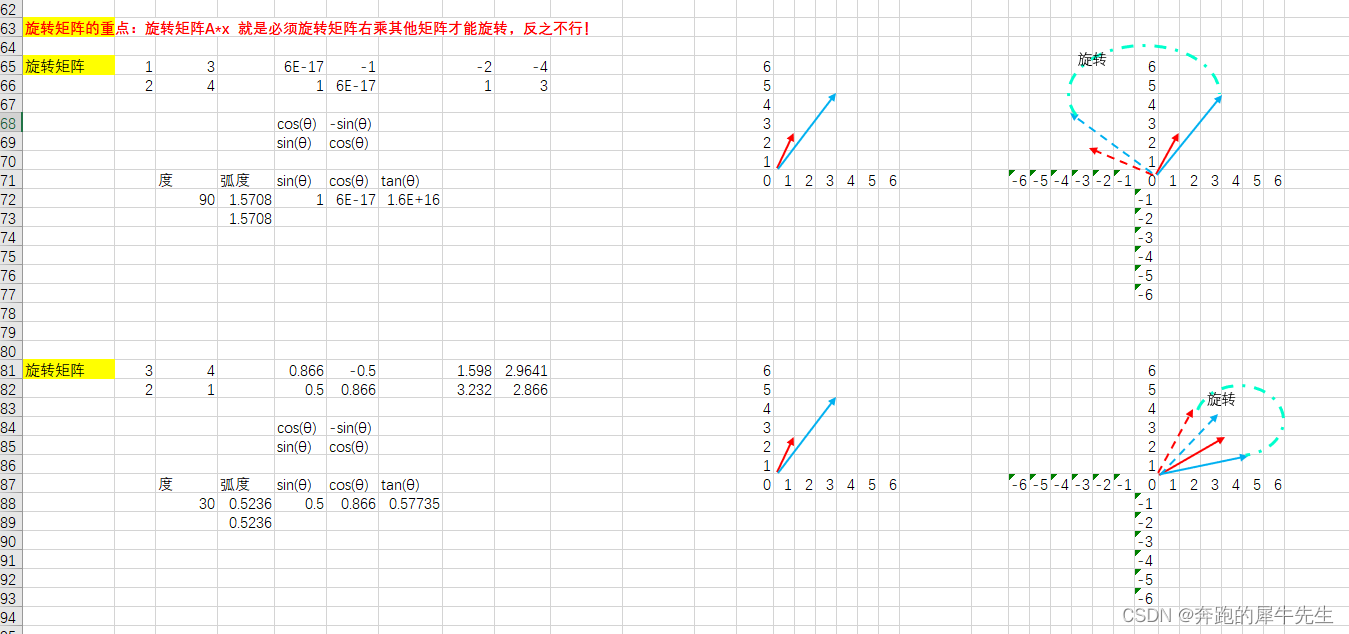
5.3 旋转矩阵应用转移点： 旋转矩阵右乘其他矩阵才可以
- 旋转矩阵的重点：旋转矩阵A*x 就是必须旋转矩阵右乘其他矩阵才能旋转，反之不行！
6 伸缩矩阵
放大缩小倍数矩阵
- 把[1,0;0,1] 变成[2,0;0,1]，即可实现伸缩效果
- 比如变成[2,0;0,1]，是第1个列向量变长2倍
- 比如变成[1,0;0,-2]，是第2个列向量变长2倍，且方向要相反（向原点的另外一边）
- 正负号实现，同方向，或反方向
- 数值大小>1实现放大效果，反之<1是缩小效果
$$
\left[
\begin{matrix}
2 & 0 \\
0 & 1 \\
\end{matrix}
\right]
$$
7 剪切矩阵
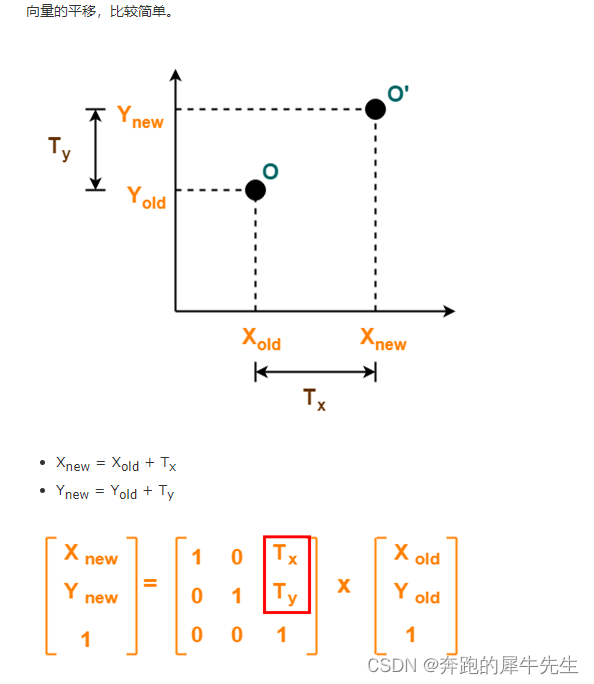
8 平移矩阵？？？
https://www.cnblogs.com/meteoric_cry/p/7987548.html
https://www.cnblogs.com/meteoric_cry/p/7987548.html
