二叉堆
- 二叉堆自我调整
- 插入节点(上浮)
- 删除节点(下沉)
- 构建二叉堆(所有非叶子节点依次“下沉”)
二叉堆本质上是一种完全二叉树,它分为两个类型。
- 最大堆
- 最小堆
最大堆的任何一个父节点的值,都大于或等于它左、右孩子\节点的值
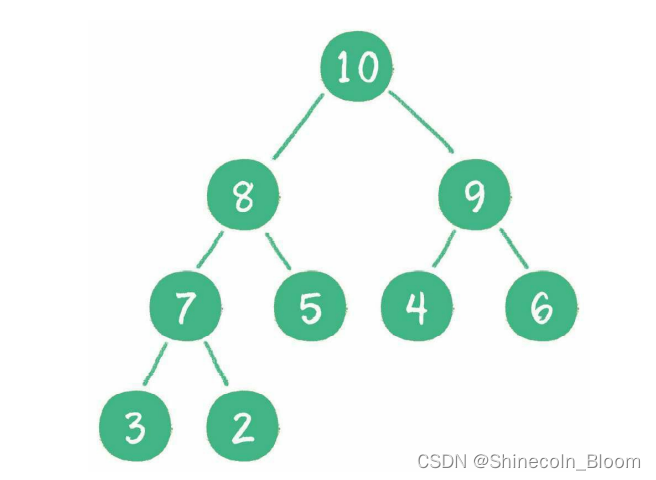
最小堆的任何一个父节点的值,都小于或等于它左、右孩子节点的值。
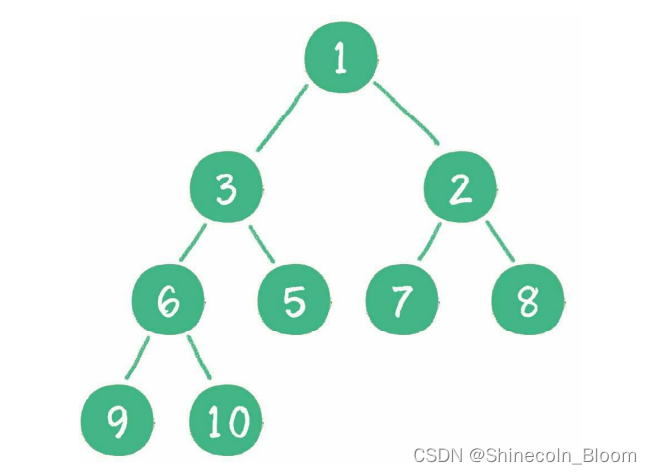
二叉堆的根节点叫作堆顶。
最大堆和最小堆的特点决定了:最大堆的堆顶是整个堆中的最大元素;最小堆的堆顶是整个堆中的最小元素。
二叉堆自我调整
堆的自我调整,就是把一个不符合堆性质的完全二叉树,调整成一个堆。
- 插入节点
- 删除节点
- 构建二叉堆
插入节点(上浮)
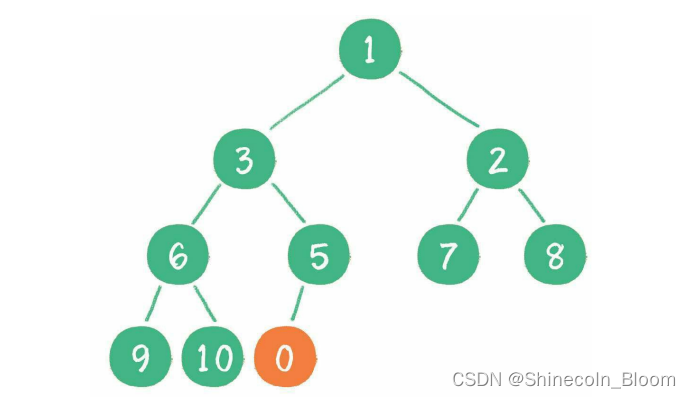
当二叉堆插入节点时,插入位置是完全二叉树的最后一个位置。
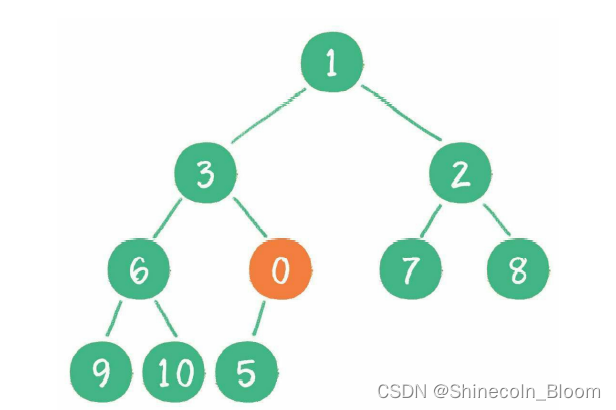
这时,新节点的父节点5比0大,显然不符合最小堆的性质。于是让新节点“上浮”,和父节点交换位置。
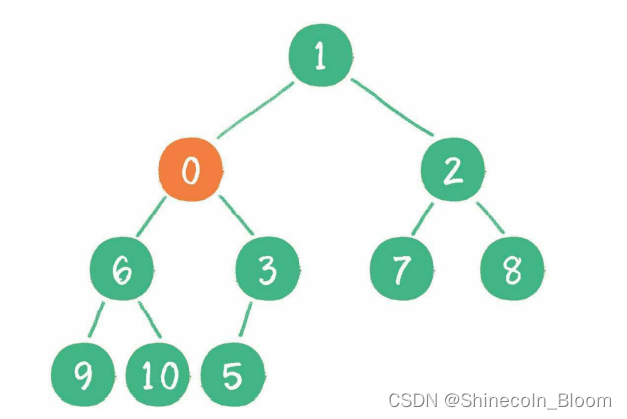
继续用节点0和父节点3做比较,因为0小于3,则让新节点继续“上浮”。
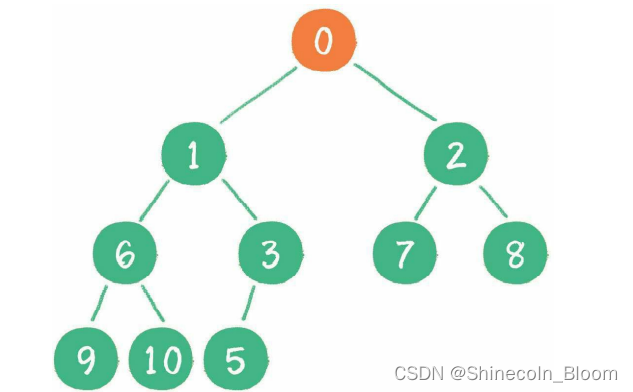
继续比较,最终新节点0“上浮”到了堆顶位置。
/**
* 插入元素的位置是数组的最后一个位置。
* 插入(上浮)
* @param array
*/
public static void upAdjust(int[] array){
//插入位置都是在数组的末尾,所以array.length-1就是当前插入位置的数组下标.
int childIndex = array.length-1;
//左孩子的父节点下标
int parentIndex = (childIndex-1)/2;
//temp 保存插入的叶子节点值,用于最后的赋值
int temp = array[childIndex];
while (childIndex>0&&temp<array[parentIndex]){
//无须真正交换,单向赋值即可
array[childIndex] = array[parentIndex];
//在和上一个父节点比较。。。
childIndex = parentIndex;
//不管上一个节点是左孩子还是右孩子,通过(parentIndex-1)/2都可找到父节点的父节点。。
parentIndex = (parentIndex-1)/2;
}
//找到childIndex,把值temp插入
array[childIndex] = temp;
}
删除节点(下沉)
所删除的是处于堆顶的节点。
把堆的最后一个节点10临时补到原本堆顶的位置。
/**
* 删除(下沉)
* @param array 待调整的堆
* @param parentIndex 要“下沉”的父节点
* @param length 堆的有效大小
*/
public static void downAdjust(int[] array,int parentIndex,int length){
//temp 保存需要下沉的父节点值,用于最后的赋值
int temp = array[parentIndex];
//找到父节点的左孩子
int childIndex = 2*parentIndex+1;
while (childIndex<length){
// 如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子(需要和左右孩子中最小的交换)
if(childIndex+1<length&&array[childIndex+1]<array[childIndex]){
//定位右孩子
childIndex++;
}
// 如果父节点小于的任何一个孩子的值,则直接跳出(没有交换的必要了)
if(temp<=array[childIndex]){
break;
}
无须真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
//在基于现在往下找。。
parentIndex = childIndex;
childIndex = 2*childIndex+1;
}
//最后在将下沉的父节点赋值进去
array[parentIndex] = temp;
}
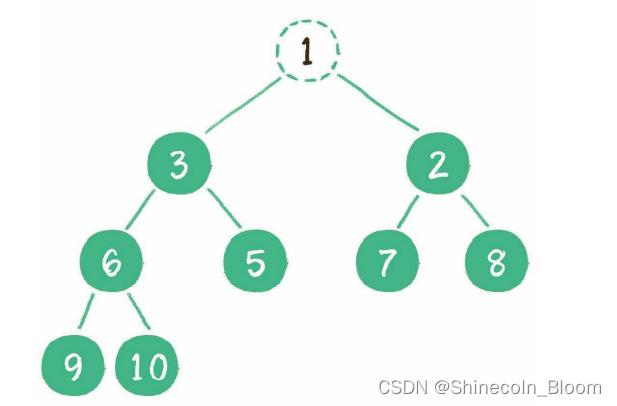
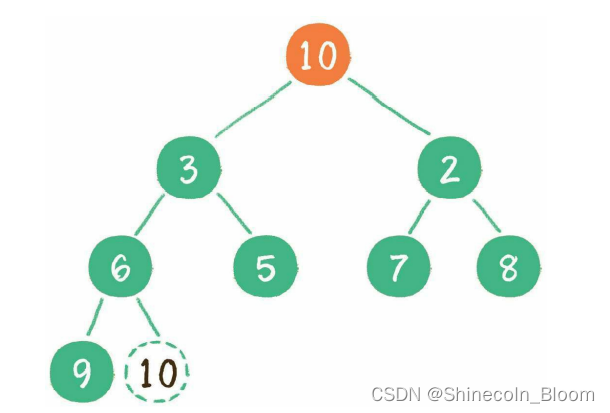
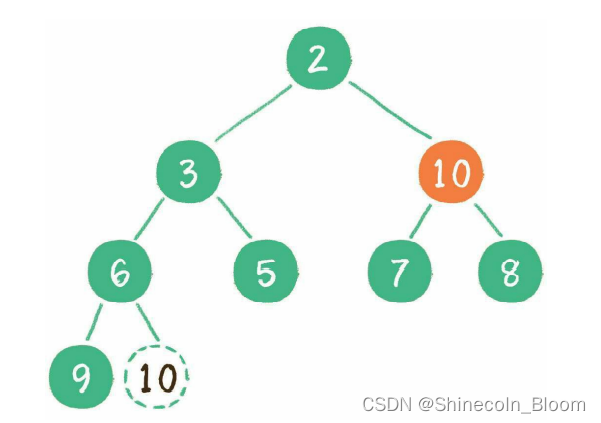
让暂处堆顶位置的节点10和它的左、右孩子进行比较,如果左、右孩子节点中最小的一个(显然是节点2)比节点10小,那么让节点10“下沉”。
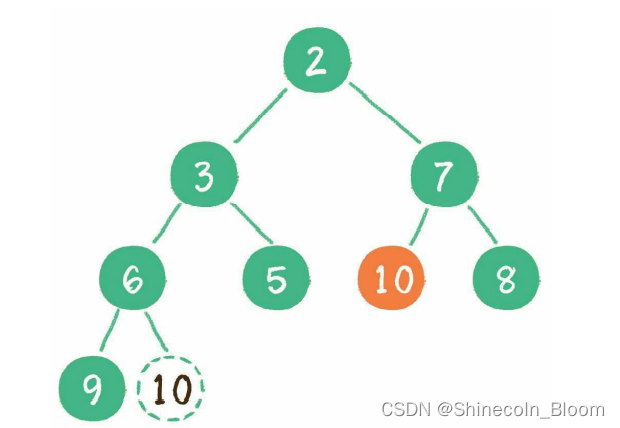
构建二叉堆(所有非叶子节点依次“下沉”)
构建二叉堆,也就是把一个无序的完全二叉树调整为二叉堆,本质就是让所有非叶子节点依次“下沉”。
public static void buildHeap(int[] array){
// 从最后一个非叶子节点(array.length-2)/2)开始,依次做“下沉”调整
for (int i = (array.length-2)/2;i>=0;i--){
downAdjust(array,i,array.length);
}
}
其中:
/**
* 删除(下沉)
* @param array 待调整的堆
* @param parentIndex 要“下沉”的父节点
* @param length 堆的有效大小
*/
public static void downAdjust(int[] array,int parentIndex,int length){
//temp 保存需要下沉的父节点值,用于最后的赋值
int temp = array[parentIndex];
//找到父节点的左孩子
int childIndex = 2*parentIndex+1;
while (childIndex<length){
// 如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子(需要和左右孩子中最小的交换)
if(childIndex+1<length&&array[childIndex+1]<array[childIndex]){
//定位右孩子
childIndex++;
}
// 如果父节点小于的任何一个孩子的值,则直接跳出(没有交换的必要了)
if(temp<=array[childIndex]){
break;
}
无须真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
//在基于现在往下找。。
parentIndex = childIndex;
childIndex = 2*childIndex+1;
}
//最后在将下沉的父节点赋值进去
array[parentIndex] = temp;
}
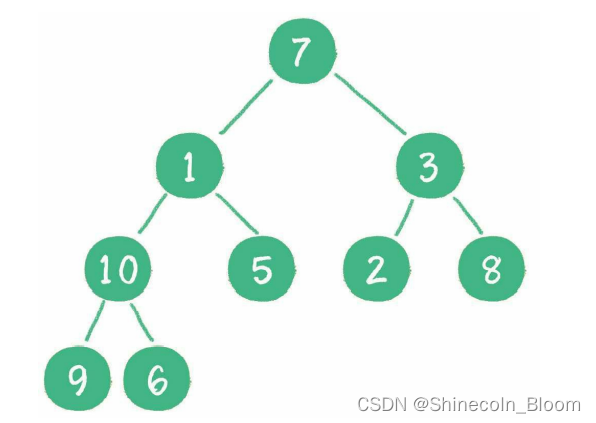
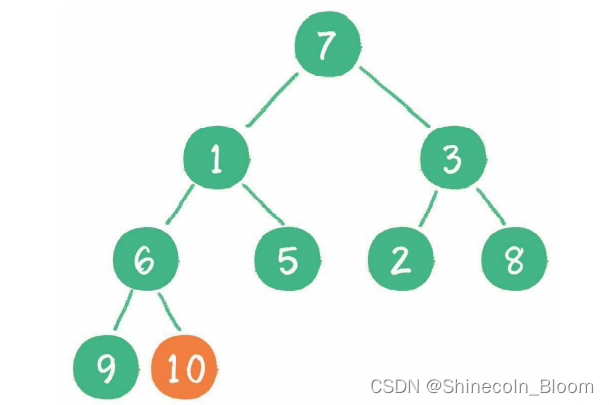
从最后一个非叶子节点开始,也就是从节点10开始。
接下来轮到节点3,
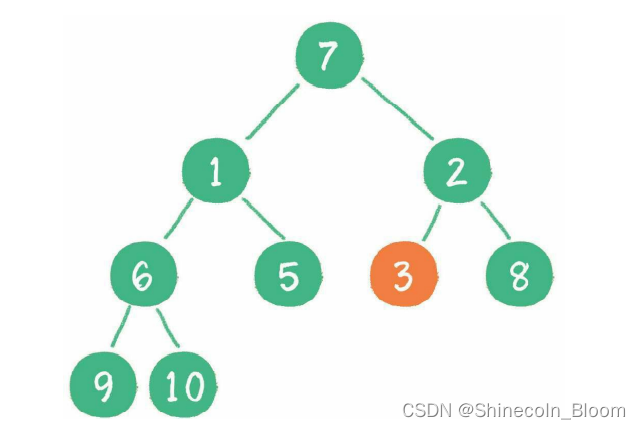
然后轮到节点1,
接下来轮到节点7,
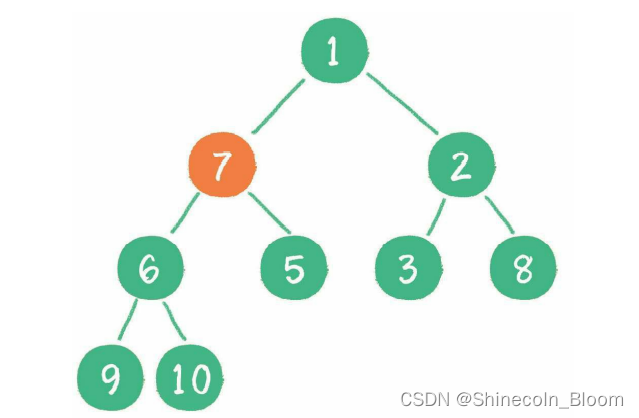
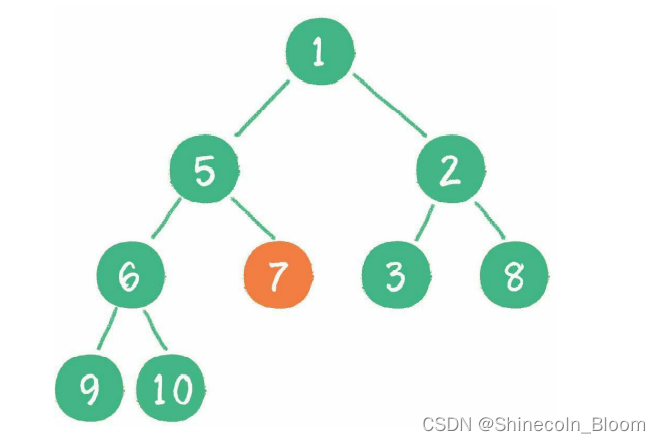
经过上述几轮比较和“下沉”操作,最终每一节点都小于它的左、右孩子节点,一个无序的完全二叉树就被构建成了一个最小堆。
总结:
堆的插入操作是单一节点的“上浮”,堆的删除操作是单一节点的“下沉”,这两个操作的平均交换次数都是堆高度的一半,所以时间复杂度是O(logn)。
至于堆的构建,需要所有非叶子节点依次“下沉”,所以我觉得时间复杂度是O(n)。
二叉堆虽然是一个完全二叉树,但它的存储方式并不是链式存储,而是顺序存储。换句话说,二叉堆的所有节点都存储在数组中。
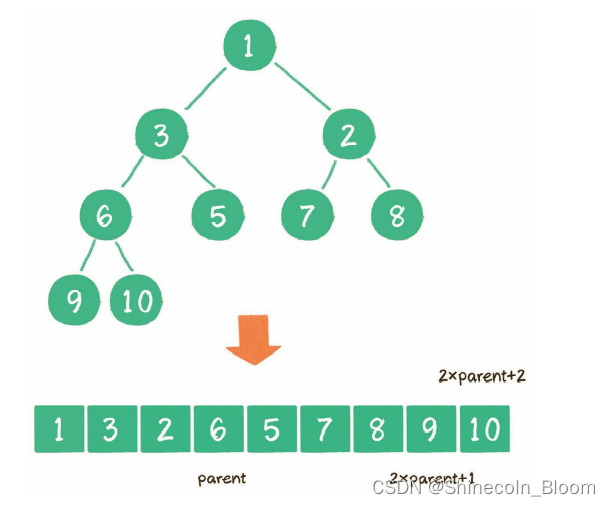
类似于层序遍历。。。。。
父节点的下标是parent,那么它的左孩子下标就是 2×parent+1;右孩子下标就是2×parent+2。
在父节点和孩子节点做连续交换时,并不一定要
真的交换,只需要先把交换一方的值存入temp变量,做单向覆盖,循环结束后,再
把temp的值存入交换后的最终位置即可。
二叉堆是实现堆排序及优先队列的基础