作为拿破仑的老师和“法国牛顿”，拉普拉斯在数学和天体力学中贡献颇多，但其实在图像处理中也会发现拉普拉斯的身影。怎么它又可以用来检测斑点，又可以检测边缘，又可以金字塔重建，还可以平滑，还可以增强细节。

其实很多拉普拉斯出现的地方都归结于拉普拉斯算子，如果没有深刻地理解拉普拉斯算子，就容易一头雾水，容易“着相”，现在我们就尝试将它”打回原形“。

拉普拉斯算子Laplace operator

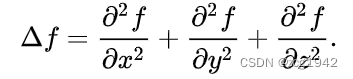
看着很简单，就是三维函数在三个方向的二阶导数之和。但其为什么说它是梯度的散度？当它等于0时意味着什么？ 

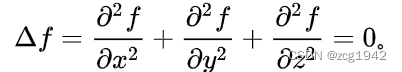
首先要清楚什么是梯度Gradient。梯度是函数“最陡”，变化最快的方向（所以有梯度下降法）。这表明它其实是一个vector operator，对平面二维图像，分布求x,y方向的梯度，然后梯度大小和正交基就可以得到一个梯度场。

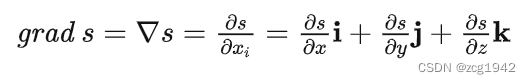
散度Divergence 是形容向量场的，从通量的角度理解，是形容一个点是否有“溢出”。因为内积表示投影，那么将向量函数与单位向量做内积，就得到该处溢出的大小。所以散度可以将由向量得到一个标量。

如果向量函数和单位向量用一套正交基，内积的结果就是各个维度的大小之和：

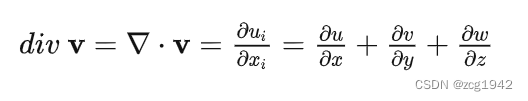
 那么，对梯度构成的向量场求散度，需要再求导一次（二阶导），就得到：

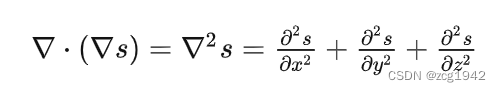
现在再回过头来看拉普拉斯算子，它是将梯度场看作一个向量场，然后求它的散度，所以描述的是这一点梯度“溢出”的大小。求散度的过程需要再进行一次微分，所以这就是为什么把拉普拉斯算子比做加速度的原因。

拉普拉斯边缘检测

下面是一个渐变的边缘检测示意图，分别可以用一阶和二阶算子计算边缘。

一阶的话，可以使用梯度的极值表示边缘；一阶导数通常会产生较宽的边缘。

二阶的话，可以使用拉普拉斯响应的过零点表示边缘

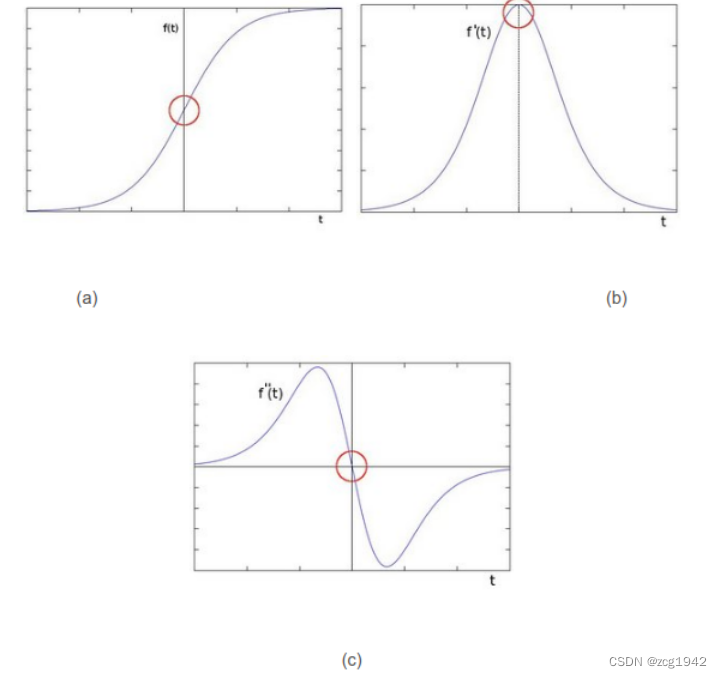
 现在尝试从散度的角度理解。梯度场方向都是向右，但是强度先是渐强，然后减弱。渐强的过程中二阶导数为正，流出大于流入，所以散度是正的；减弱的过程正好相反。

拉普拉斯斑点检测

刚才只是沿着边缘垂直方向的情况，当把边缘替换成斑点时，从各个方向上的移动时拉普拉斯响应都会像是刚才一样变化，这时的波峰波谷就形成了山峰和山谷。所以当使用拉普拉斯极值点的时候就可以实现斑点检测。

下图可以看到峰谷对应的散度值。可以理解为什么拉普拉斯算子的极值点是斑点，零点又可以做边缘检测。

拉普拉斯边缘检测模板

将拉普拉斯算子看作是二阶导在多维的拓展，那么拉普拉斯算子的过零点就可以用来做边缘检测。

有限差分算子，可以由二阶导定义或者泰勒展开推导出。

需要说明的是，拉普拉斯滤波器模板与图像的卷积是拉普拉斯响应，结果有正负之分，为了显示还需要归一化到0~255。但归一化之后反而不太好找过零点了。

拉普拉斯滤波器本质是一个带通滤波器，因为平坦处响应为0，高频处响应也为0（过零点）。

高斯拉普拉斯LoG

因为二阶导对噪声敏感，所以一般会先使用高斯模糊，然后再在平滑后的结果上使用拉普拉斯算子。高斯和拉普拉斯都是算子，根据卷积的结合律，可以提前计算高斯滤波的拉普拉斯响应，这样节约了计算量。

画出图像是墨西哥草帽：

墨西哥草帽和图像做相关就可以实现斑点检测（结合极大值的寻找），这就是SIFT检测的基本原理。结合离散拉普拉斯滤波算子可以看出，极大值处对应高亮背景中的黑点，极小值对应暗黑背景中的高亮点。LoG中的sigma则表示了斑点中的scale。

差分高斯金字塔

LoG可以使用DoG近似。DoG是不同的尺度因子，所以两个高斯滤波核中心会错位，二者做差就类似拉普拉斯中的左右或者上下做差。因为高斯滤波是低通，两个低通做差来近似拉普拉斯滤波器，也解释了拉普拉斯滤波器带通的性质。

拉普拉斯金字塔

在拉普拉斯金字塔中，每层是图像做差得到的结果。看到图像之差，就很自觉地联系到拉普拉斯算子的近似了。

拉普拉斯用于图像重建，重建的意义是恢复到原始状态，而一旦有了下采样再上采样就会有信息丢失，所以拉普拉斯其实提前记录了这一损失，这样就可以放心去下采样了。

除了重建，拉普拉斯金字塔又进一步用在图像融合。其实就是在重建的过程中同时使用两个图像的拉普拉斯金字塔，因为在多尺度上进行，所以一般可以得到较好的融合效果。

融合多通道图时不能分通道融合，因为不同通道的频率信息不完全一致，融合结果会破坏颜色比例，导致最终的结果出现色差。同时在融合的过程中，差分图像的精度可能损失，在底图融合时mask精度不够会在融合极大值极小值的工程中插值出预期之外的值，在之后的融合过程中继续放大误差。

reference：

https://www.plymouth.ac.uk/uploads/production/document/path/3/3744/PlymouthUniversity_MathsandStats_the_Laplacian.pdf

三大偏微分方程之首：拉普拉斯方程(1) - 知乎

基础篇2: 梯度、散度与旋度 - 知乎

高斯拉普拉斯算子（Laplacian of Gaussian, LoG） - 知乎

DoG和LoG算子 - 知乎

https://www.cse.psu.edu/~rtc12/CSE486/lecture11.pdf

Spatial Filters - Laplacian/Laplacian of Gaussian

https://www.cnblogs.com/imageshop/p/10620935.html