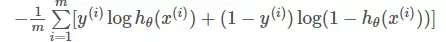一、Matlab编程 微分方程、SS模型、TF模型、ZPK模型的关系

以最简单的单自由度振动模型为例：


以上表示u(t)线性组合输入系统（这里是3u(t)）时求系统的响应（即输出函数y(t)）
SS模型也可转成TF模型：
tf(ss(A,B,C,D))
TF转零极点增益ZPK模型
[z p k]=tf2zp([3],[1 0 4])
z =
Empty matrix: 0-by-1
p =
0 + 2.0000i
0 - 2.0000i
k =
3
即

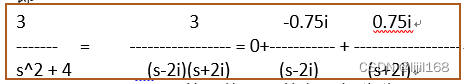
还可以用residue函数将传递函数变成部分分式展开式
[z p k]=residue([3],[1 0 4])
z =
0 - 0.7500i
0 + 0.7500i
p =
0 + 2.0000i
0 - 2.0000i
k =
[]

二、对系统输出进行微分计算

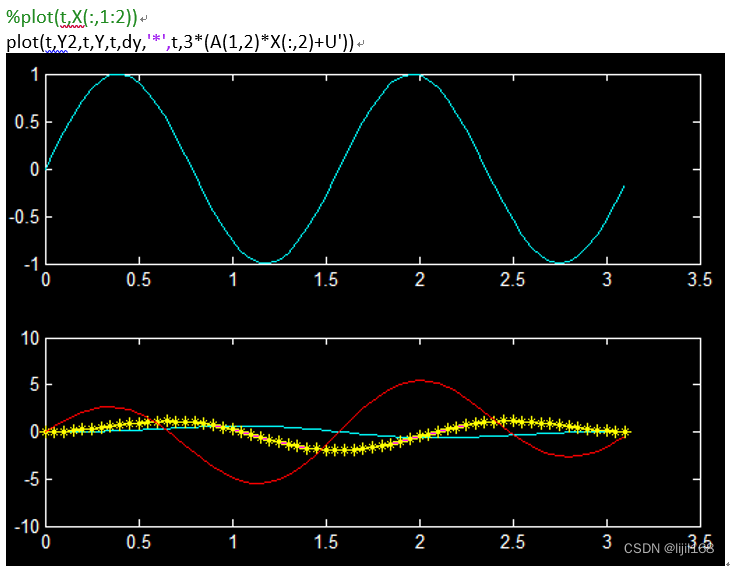
三、对系统输出进行积分计算

2.设原系统输出为y1(t),怎么求其积分y1_(t)?


所以对原系统而言，相当于多了个积分状态参数。
其输出函数为y1_(t)=3x3
Matlab编程验证：
subplot(4,1,3)
[A2,B2,C2,D2]=tf2ss([3],[1 0 4])
Sys=ss(A2,B2,C2,D2);
tf(ss(A2,B2,C2,D2))
[Y,t,X]=lsim(Sys,U,t,[0 0]);
plot(t,Y,t,3X(:,1))
[A2,B2,C2,D2]=tf2ss([3],[1 0 4 0])
Sys=ss(A2,B2,C2,D2);
tf(ss(A2,B2,C2,D2))
[Y,t,X]=lsim(Sys,U,t,[0 0 0]);
subplot(4,1,4)
plot(t,Y,t,3*X(:,1:2))

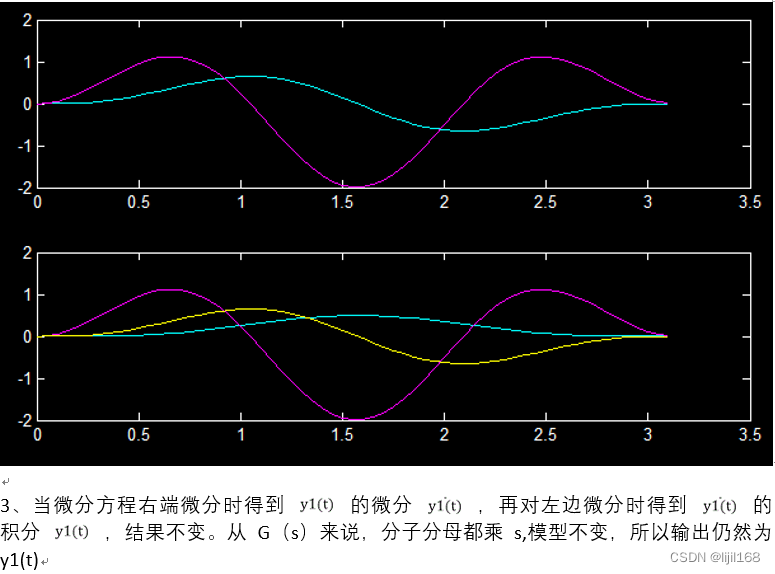
四、总结

对系统求微分，传递函数乘s，对系统求积分 ，传递函数乘1/s。

五、系统的零点与极点的物理意义参考 ：https://www.zhihu.com/question/22031360/answer/3073452777