题目描述

原题链接

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释： 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

提示：

2 <= numbers.length <= 3 * 104
-1000 <= numbers[i] <= 1000
numbers 按 非递减顺序 排列
-1000 <= target <= 1000
仅存在一个有效答案

双指针法

思路分析

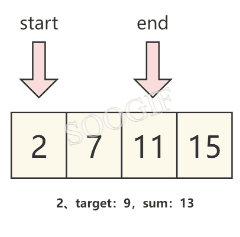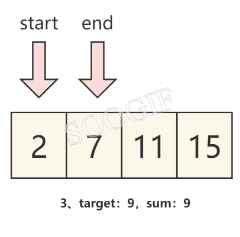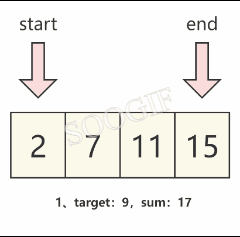
我们观察题目可以发现，数组是已经排好序的，那么我们可以直接定义两个元素来分别指向 数组头 和 数组尾 ，然后循环使两个指针移动，直到最终算出我们需要的结果。

假设左指针为start，右指针为end，并将左右指针所对应的元素的和设为sum，那么我们就可以发现：

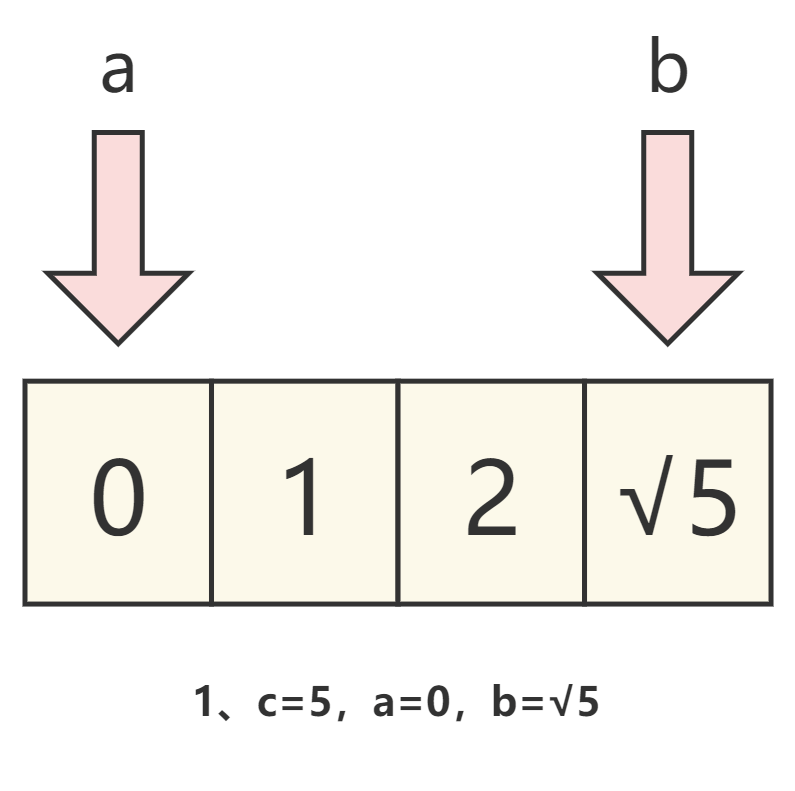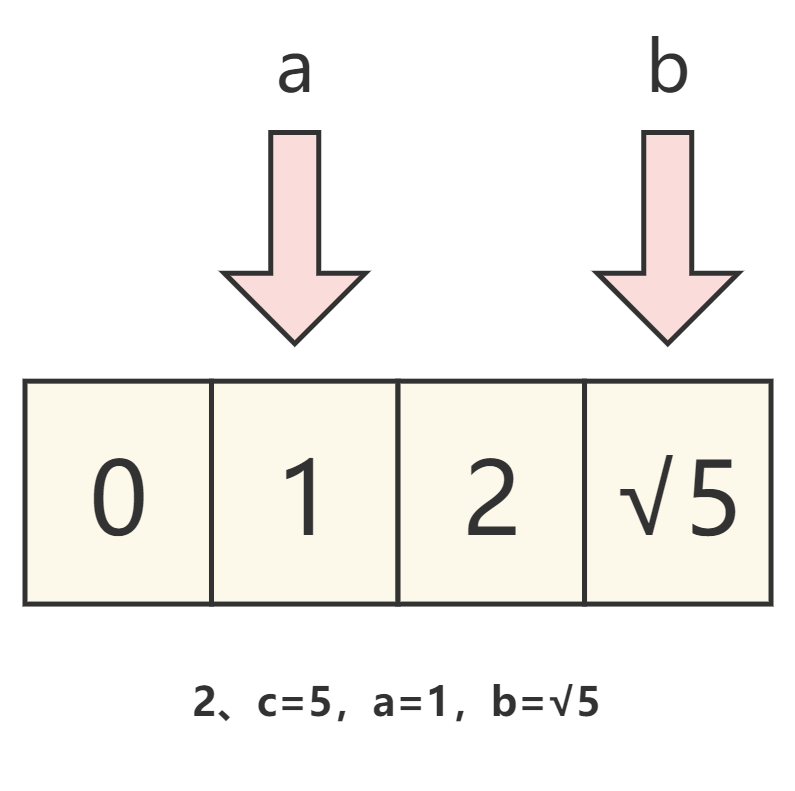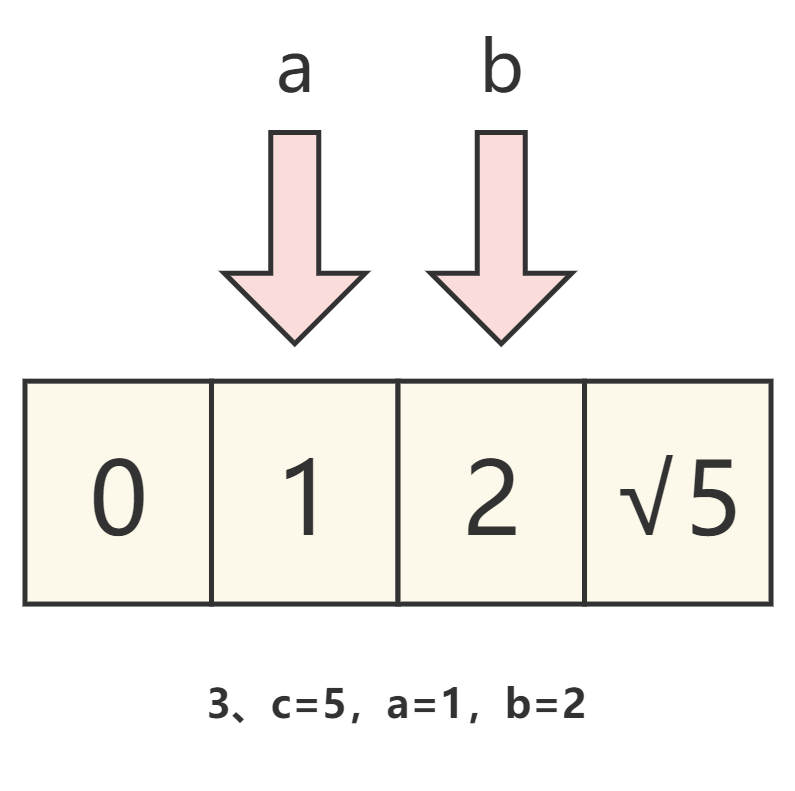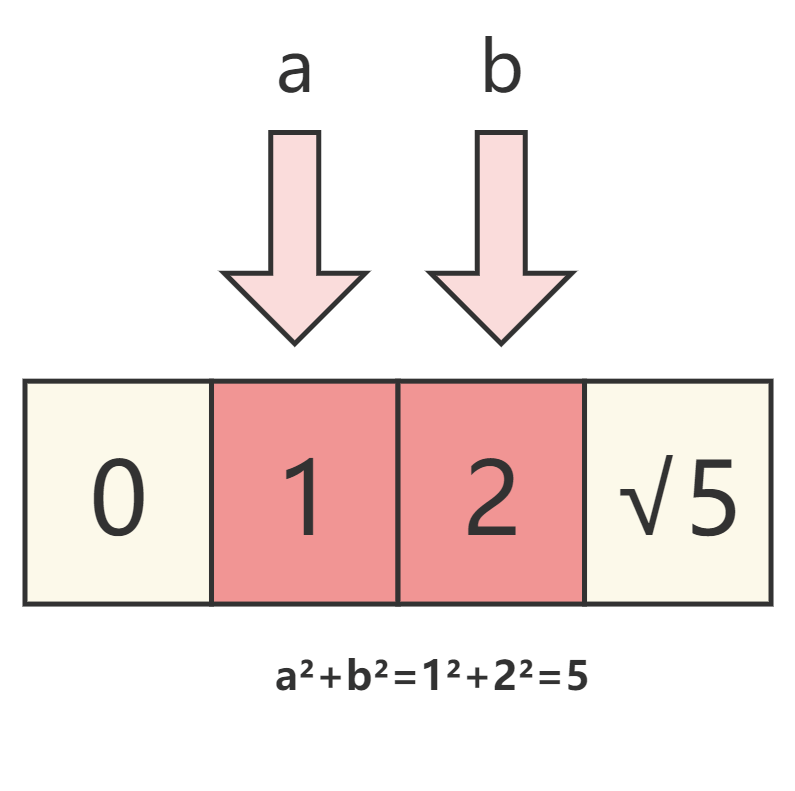
当 sum==target 时，就可以得到我们需要的结果
当 sum>target 时，我们需要将右指针对应的元素变小一些，那么就需要 将右指针向左移动一个元素，也就是 end--
当 sum<target 时，我们需要将左指针对应的元素变大一些，那么就需要 将左指针向右移动一个元素，也就是 start++

我们可以通过下图来理解这个规律。

图解

双指针法.gif

代码实现

public int[] twoSum(int[] numbers, int target) {
    if (null == numbers) {
      return new int[0];
    }
    int start = 0;
    int end = numbers.length - 1;
    while (start < end) {
        int sum = numbers[start] + numbers[end];
        if (sum == target) {
            return new int[]{start + 1, end + 1};
        } else if (sum > target) {
            end--;
        } else {
            start++;
        }
    }
    return new int[0];
}

二分查找法

思路分析

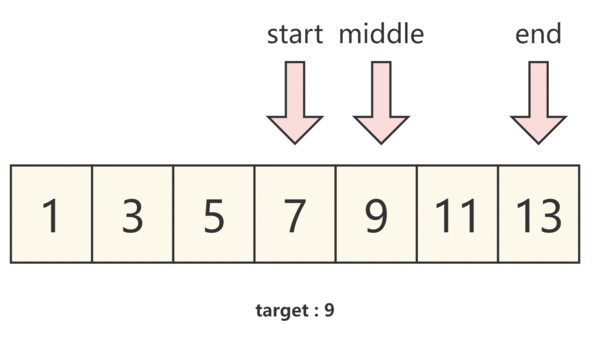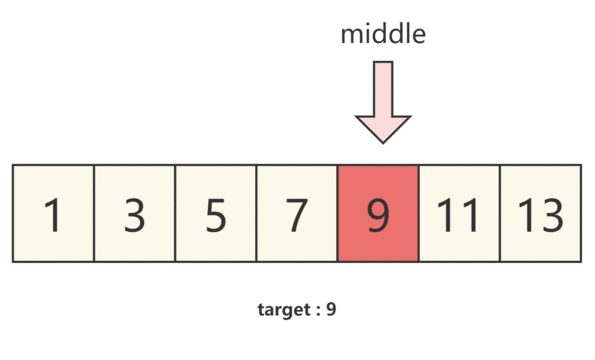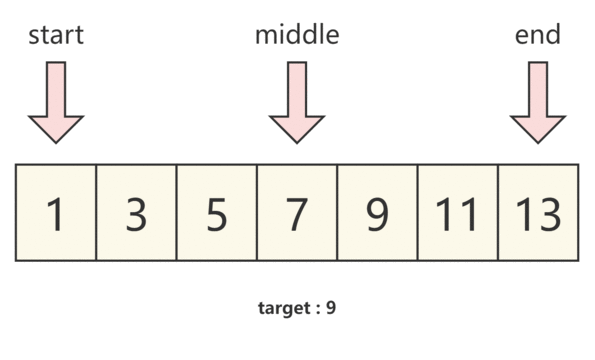
那么我们将题目带入，假设左指针为 start，右指针为 end，并将左右指针中间的下标为 middle，即可得到：

当 numbers[middle]==target 时，我们即可得到需要的结果
当 numbers[middle]>target 时，说明 中间数大于预期结果，结果在左半部分，那么我们需要 将右指针移动至middle的位置，并重新取middle的位置。
当 numbers[middle]<target 时，说明 中间数小于预期结果，结果在右半部分，那么我们需要 将左指针移动至middle的位置，并重新取middle的位置。

我们通过下图来理解。

图解

代码实现

public int[] twoSum(int[] numbers, int target) {
        if (null == numbers) {
            return new int[0];
        }
        for (int i = 0; i < numbers.length; ++i) {
            int start = i + 1;
            int end = numbers.length - 1;
            while (start <= end) {
                int middle = (end - start) / 2 + start;
                if (numbers[middle] == target - numbers[i]) {
                    return new int[]{i + 1, middle + 1};
                } else if (numbers[middle] > target - numbers[i]) {
                    end = middle - 1;
                } else {
                    start = middle + 1;
                }
            }
        }
        return new int[0];
    }