Problem: 283. 移动零

思路

首先我们来讲一下本题的思路

• 本题主要可以归到【数组划分/数组分块】这一类的题型。我们将一个数组中的所有元素划分为两段区间，左侧是非零元素，右侧是零元素

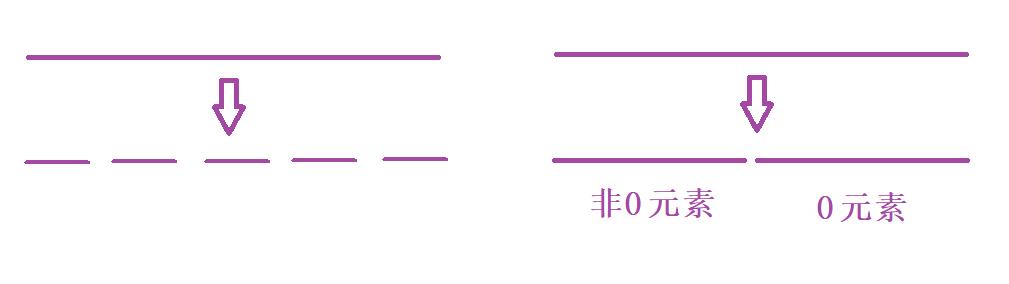
• 那解决这一类的题我们首先想到的就是【双指针算法】，学习过C语言的同学应该就可以知道指针是比较繁琐和复杂，如果有兴趣学习的同学可以看看我的这篇文章 链接
• 不过在这里呢我们不需要去使用int*这种指针，而是直接使用数组下标来充当指针即可

好，那我们就来看看这个双指针到底是怎样的，要如何去使用

• 两个指针的作用
  • 【cur】： 从左往右扫描数组，遍历数组
  • 【dest】：已处理的区间内，非零元素的最后一个位置
• 可以看到，cur是我们用来遍历数组的，从[cur, n - 1]就是还未处理的元素；那么从[0, cur]就是已经处理过的元素，但是呢本题的要求是我们要划分出【零元素】与【非零元素】，所以呢前面的区间我们可以再度划分为[0, dest]和[dest + 1, cur - 1]

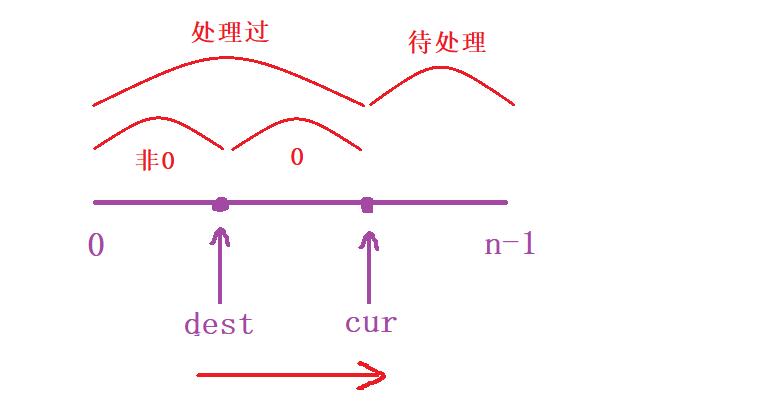
小结一下：

[0, dest] [dest + 1, cur - 1] [cur, n - 1]

• [0, dest] —— 非零元素
• [dest + 1, cur - 1] —— 零元素
• [cur, n - 1] —— 未处理元素

算法图解分析

接下去我们就通过画算法图解的形式来模拟一下解题的过程

• 我们就以题目中所给出的第一个示例为例来进行讲解，因为在一开始我们还没处理过任何的非零元素，所以对于[0, cur - 1]这段区间是没有任何数据的，所以在一开始我们可以将【dest】这个指针置于-1的位置

• 因为我们需要将非0元素移动到前面，所以呢如果遇到了0元素的话，cur++即可，将其留在这个位置上

• 那当我们遇到非0元素时，就需要将其交换到前面去，那我们[0, dest]这个区间就是用来存放非0元素的，此时多了一个元素的话那dest就要加1，原本其是指向-1这个位置，那我们可以使用++dest来完成

• 接下去，当数据交换过来后，我们可以去对照上面的这三个区间，可以发现最左侧是非0元素，中间是0元素，右侧呢则是待处理的元素。接下去我们又碰到了0元素，所以cur++

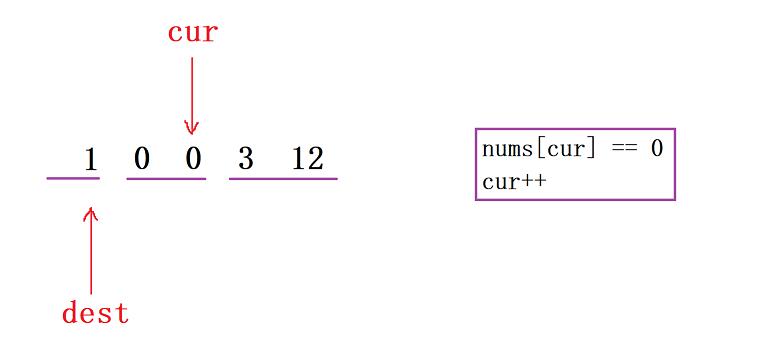
• cur再后移之后呢，我们又碰到了非0元素，继续让dest上来然后交换二者位置上的元素

• 那现在我们再来看这三个区间，左侧还是保持为【非0元素】，中间为【0元素】，右侧的话则是【待处理的元素】

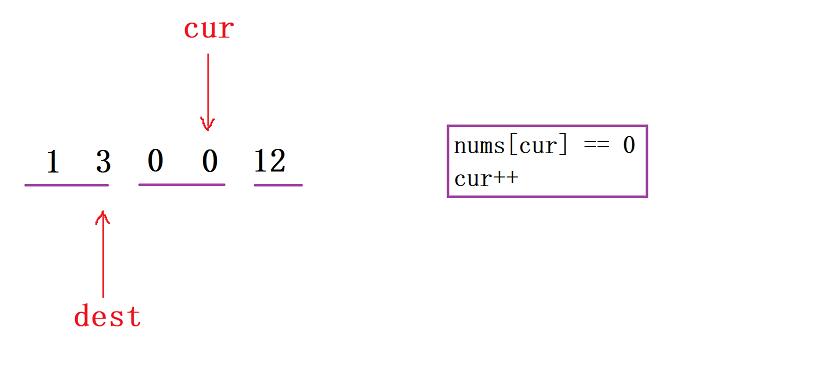
• 然后碰到非0元素后，继续让++dest，然后做交换

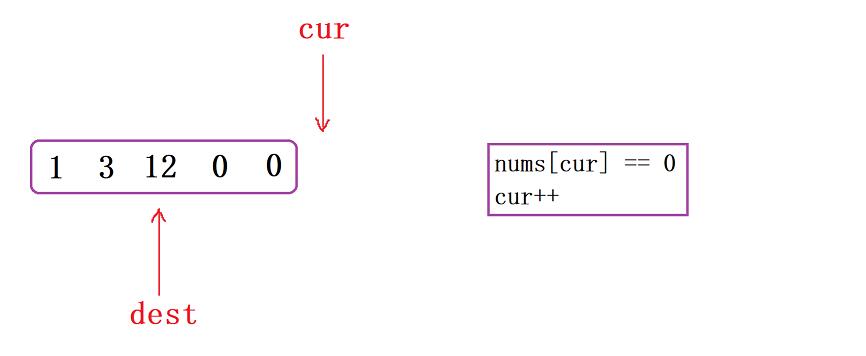
• 最后的话我们来看看这个处理完后的整个区间元素：非0元素都在前面，而0元素则都在后面，[cur, n - 1]的这段区间也不存在了，说明已经没有待处理元素了

复杂度

接下去我们来分析一下本题的时空复杂度

• 时间复杂度:

本算法的核心思路参考的是【快速排序】的区间划分，我们这里就是在不断遍历数组的过程中，以中间的0作为分割，然后左侧是非0元素，右侧是未处理的元素。在处理的过程中我们只是遍历了一次这个数组，所以复杂度为 $O(n)$

• 空间复杂度:

在本题中我们并没有去开出额外的空间，所以复杂度为 $O(1)$

Code

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        for(int dest = -1, cur = 0; cur < nums.size(); ++cur)
        {
            if(nums[cur] != 0)
            {
                swap(nums[++dest], nums[cur]);
            }
        }
    }
};