滤波

  电子设备的功耗信息可以由电路运行时的电压、电流和电路的阻抗联合计算得到，而且纯电阻运行期间的功耗会转换为热能。在研究中，一个器件的功耗与整个加密设备的功耗成正相关；若该期间的功耗增加，则整个加密设备的功耗也成一定比例增加，反之亦然。因此，研究只需要采集一个元器件的功耗，进而观察整个设备的功耗情况。
  功耗曲线采用最为传统而简单有效的方式进行采集，即，在电源端串联一个 $1-15\Omega$ 的采样电阻，当加密设备工作时，使用高精度抗干扰的探测器采集采样电阻两端的电压，则此时的功耗可通过下式计算得到。
$$P=\frac{U^2}{R}$$
其中，$U$ 为运行电压， $R$为采样电阻， $P$为采样电阻的功耗，借此观察整个设备的功耗情况。然而，实际采集到的功耗存在大量的加性噪声，故采集到的功耗曲线可由下式表示：
$$F(n)=S(n)+N(n)$$
其中， $F(n)$为实际采集到的功耗曲线， $S(n)$ 为原始功耗信息，$N(n)$ 为噪声信息。噪声信息可将其详细分为如下部分：
（1）电源噪声
  在实际电路中，给加密设备提供的电源不可能是理想电压源，电源都存在噪声；而采集的功耗曲线与电源信号直接关联，电源噪声对功耗信息有着较大的影响。因此，尽量选择较为稳定的电源作为攻击加密设备的供电电源。
（2）时钟发生器噪声
  侧信道分析攻击中，无论是加密设备的运行，还是采集设备的使用，均离不开时钟信号。如果时钟信号不稳定，可能导致采集到的功耗曲线失调，以及时钟信号可能通过元器件耦合到采集到的功耗曲线中，增加了功耗曲线的处理难度。设备时钟信号来源一般是晶振。
（3）量子化噪声
  量子化噪声是在采集功耗信息时，信号通过模数转换器时产生。采集设备的模数转换器分辨率越高，其采集到的信号越接近实际信号，因其产生的量子化噪声量越小。一般侧信道分析研究中，8位的模数转换器可满足要求。同时模数转换器还需要注意采样率，采集时需满足奈奎斯特采样定理。
（4）环境噪声
  外界环境存在大量的电子设备，其在运行时会向外辐射电磁波，电磁侧信道分析方法便是利用其原理进行分析。当加密设备处于辐射较强的环境时，环境中的电磁波可能与加密设备产生耦合，最后产生感应电场叠加在功耗信息中。因此，在采集功耗曲线时，尽量保证环境对设备的影响较小。
  功耗曲线中原始功耗信息差异性较小，其与密钥相关的特征信息淹没在电子噪声中，对后续的侧信道攻击增加了巨大的难度。例如，对采集到的功耗曲线进行频域分析

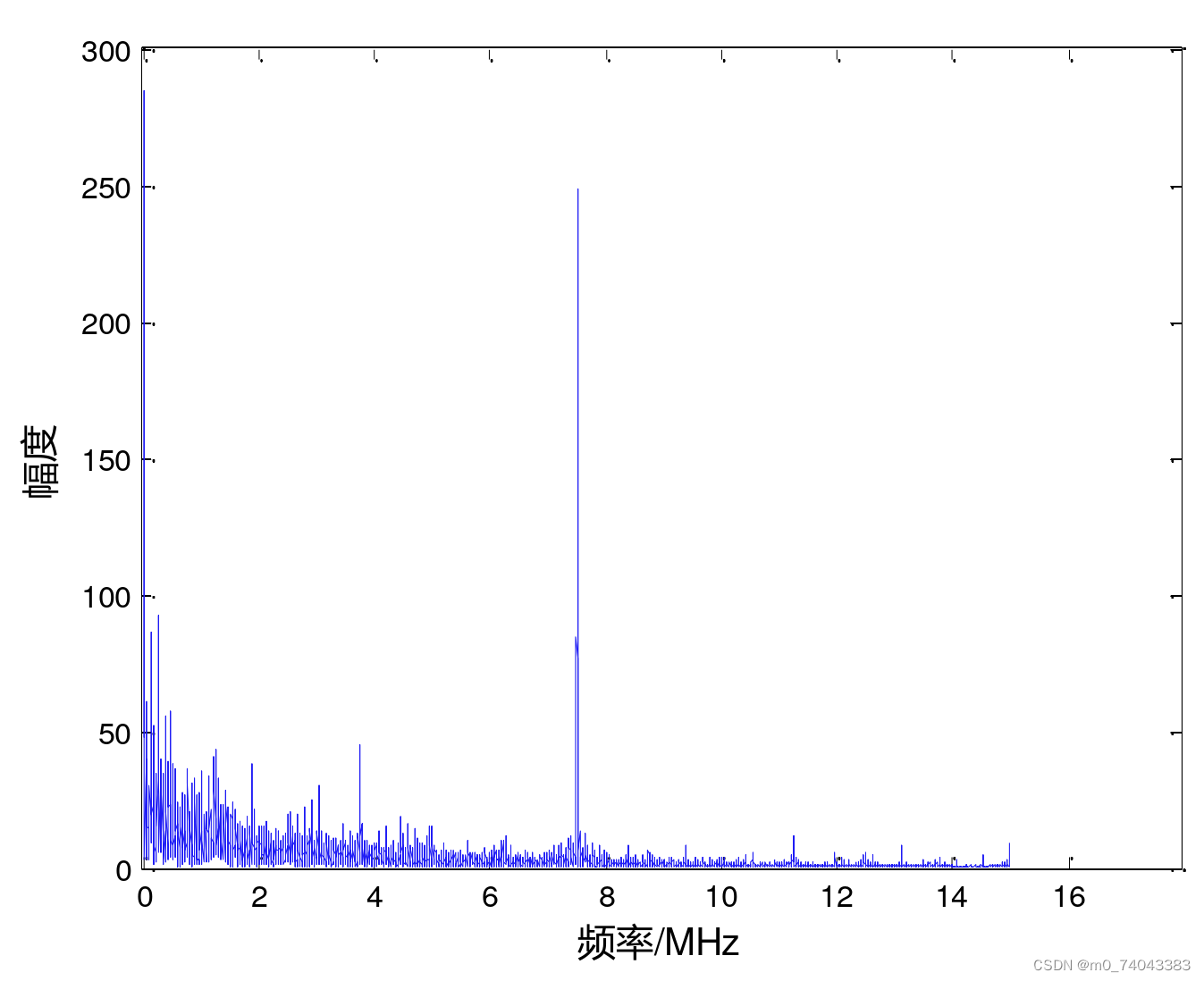
图1. 功耗曲线频谱图

  由上图1看出，频率点在 $7.3MHz$左右，存在较大的能量信息，这与采集设备的工作频率一致。信息点集中于低频部分，噪声因为设备运行频率较高而集中于高频部分，因此可选用低通滤波进行噪声处理，还可采用滑动平均进行滤波，即，通过对窗口大小范围内的波形取平均值达到滤波的效果。

对齐

  在采集功耗曲线时，常常在加密设备运行加密算法或是攻击算法处将触发引脚置于高电平，即触发采集器（如：示波器）开始采集功耗信息；在攻击算法结束处将触发引脚设置为低电平，停止采集功耗信息。由此采集到的功耗曲线不含其他与攻击算法无关的操作所产生的功耗，即可较为完全反映攻击算法运行时的功耗信息。
  然而，加密设备在受到电源不稳定，运行时钟源抖动，或是为了减少功耗信息的泄露，添加的一些与加密算法无关的操作或是数据，如：随机插入伪操作或乱序操作，攻击算法与触发点的偏移不固定，导致采集的功耗曲线错开，即功耗曲线失调。
  为了解决功耗曲线失调的问题，利用功耗曲线对齐技术对每一次迭代功耗曲线进行定位并裁剪特征攻击功耗曲线。
  对齐技术可分为：静态对齐与弹性对齐。静态对齐技术一般用于解决设备未加伪操作等防护措施，采集的功耗曲线因电源抖动等外界因素导致的功耗曲线失调问题。
  静态对齐技术一般使用模板匹配实现，即首先选取具有唯一性、数据依赖性的合适的数据作为模板，然后使用匹配算法进行功耗曲线对齐。
  详细分析步骤为：第一，攻击者选择某一条曲线中出现的一种模式；第二，尝试在所有其他功耗曲线中发现该模式，进行匹配。这意味着攻击者需要在每条曲线中确定最佳匹配选定模式的位置，然后平移各条曲线，使得该模式在曲线集的同一个位置出现。
  常见的功耗曲线对齐算法有：相关系数算法、最小二乘法、最小欧式距离法、余弦系数法以及 Tanimoto 系数法等。
（1）相关系数法
  相关系数算法主要用于计算数据间的线性关系，计算公式为：
$$\rho (X,Y)=\frac{cov(X,Y)}{\sqrt{var(X)var(Y)}}$$
取值范围为[-1,1]，相关系数绝对值越大，数据之间相关性越大，则此处为特恒功耗曲线的可能性就越大。
（2）最下二乘法
  最小二乘法是将目标功耗曲线与处理曲线之间的差值向量的平方和最小的位置作为特征匹配点。其公式为：
$$diff(X,Y)=||X-Y||$$
  为了提高实现程序的通用性，研究最小二乘法进行改进，取最小二乘的倒数为参考依据；为了防止出现除0，其分母加上常数1，公式变为：
$$dist(X,Y)=\frac{1}{1+diff(X,Y)}$$
当 $X$ 与 $Y$的差异越小，其 $dist(X,Y)$值越大，即此时处理曲线为特征功耗曲线的可能性越大。
  弹性对齐是一种动态对齐技术。静态对齐会通过横向平移波形使其在某一位置对齐，而弹性对齐会尝试改变波形每一个位置，从而使它们在所有位置对齐。因此弹性对齐可以有效地消除随机进程中断和随机时钟延时的影响。弹性对齐使用某种策略拉伸和压缩波形达到动态对齐的效果，这个过程通过对波形进行非线性重采样来实现。弹性对齐更适用于难以通过静态对齐得到对齐效果的波形。

压缩

  一个时钟周期，示波器可以采集多次，这取决于示波器的采集频率。根据奈奎斯特采样定理，采样率必须要达到采集的目标信号中最高频分量的两倍至上才能保证信号被无损的采集。而微处理器的信号时钟是由其时钟频率决定的，因此功耗信息中最主要分量频率就是时钟频率，而示波器的采样频率一般是时钟频率信号的几倍以上。基于上述原因，每一个时钟周期就采集了多个采样点，这些冗余的点含有的信息是重复的，过长的功耗曲线往往给功耗分析攻击的计算带来不必要的开销。即可通过压缩技术，可以在不大量损失泄露密钥相关信息的情况下减少功耗曲线的长度，换句话说，功耗曲线压缩技术的作用就是去掉功耗曲线中的冗余。
  为了上述目标，已知功耗曲线中各个点中包含了破解出密钥信息。《能量分析攻击》中 4.3节中关于密钥信息泄露的讨论已经表明在选用的微处理器中，这些信息主要会再能量消耗的尖峰中出现。对相关性尖峰的时钟周期进行分析后发现，功耗曲线的振幅基本正比于该时钟周期中发生的电平转换的次数，而在某一时刻时钟周期内的电平转换次数依赖于正在执行的操作，以及正在被处理的数据。所以，在不考虑高斯分布的电子噪声的情况下，功耗曲线的尖峰包含了实施功耗分析攻击所需要的全部信息。
（1）最大值提取法
  提取功耗曲线每个时钟周期内的最大位置，此时的能量消耗尖峰的值与芯片在当前时钟周期所消耗的能量成正比，因此有理由选取该点作为其所在时钟周期的代表。压缩量取决于采集目标设备时示波器的采样频率与微处理器频率的比。
（2）整合法
  该方法使用功耗曲线中尖峰及其附近的点，而不只是出现的最大尖峰的点。有效性取决于各个点的有效性，同样也依赖于信号分量和噪声分量间的大小关系。将时间间隔的长度称为阈值的话，处理的效果事实上取决于阈值的长短，而这个大小实际上很难掌握。整合方法有：原始整合、绝对值整合、平方和整合。