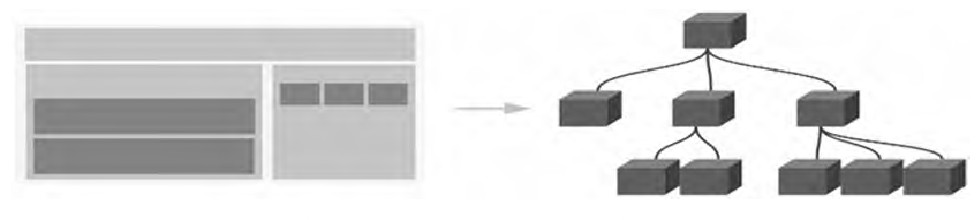
一.二叉树的种类
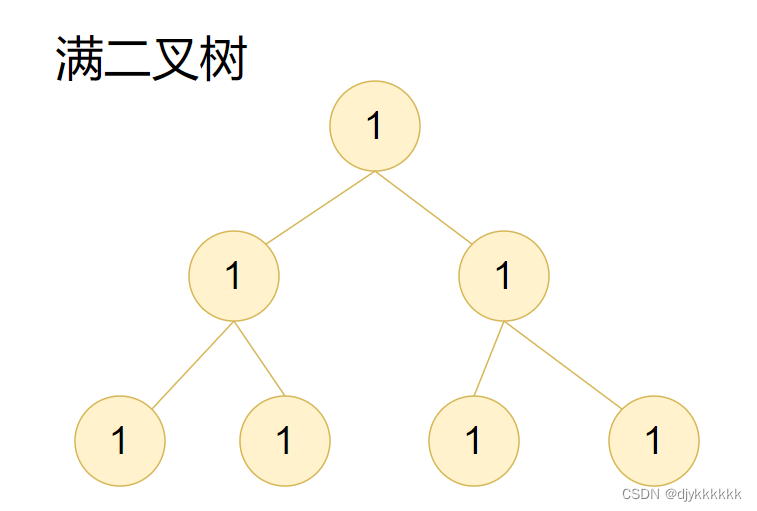
1.满二叉树:就是说每一个非叶子节点的节点都有两个子节点。
2.完全二叉树:此二叉树只有最后一层可能没填满,并且存在的叶子节点都集中在左侧!!!


(满二叉树也是完全二叉树)
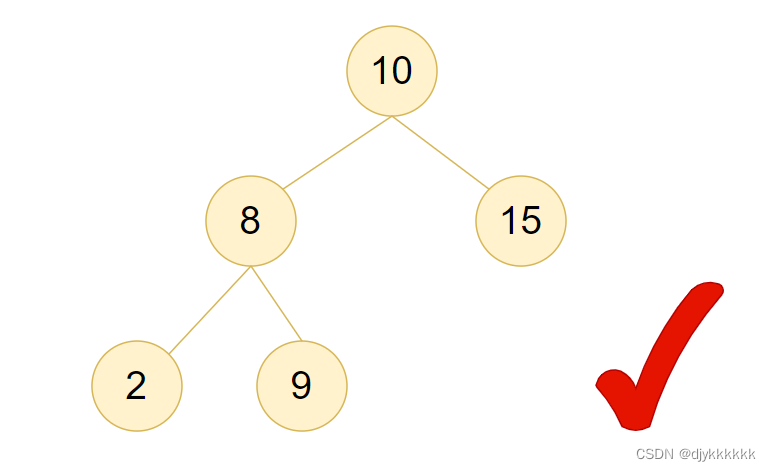
3.二叉搜索树(BST树):顾名思义,搜索是跟值相关联。
-
中间节点的左侧子树的所有节点的元素值小于中间节点的值
-
中间节点的右侧子树的所有节点的元素值大于中间节点的值
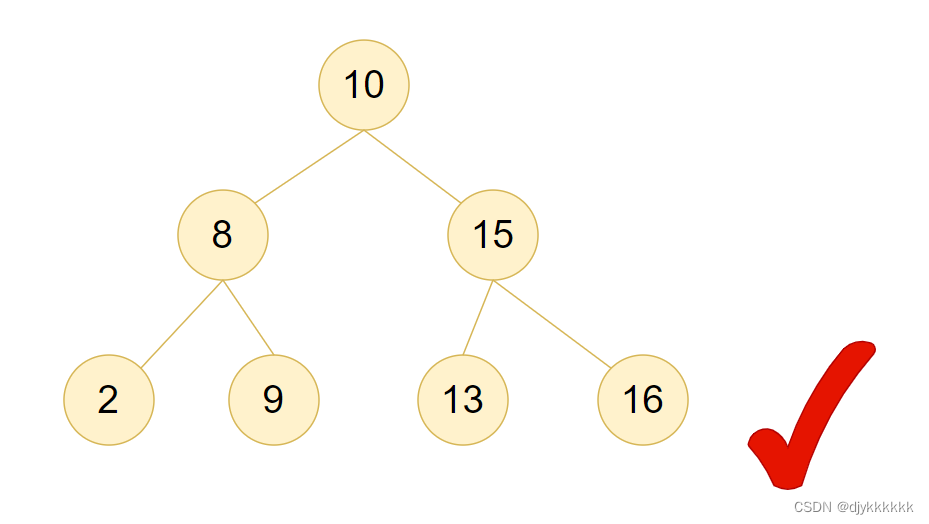
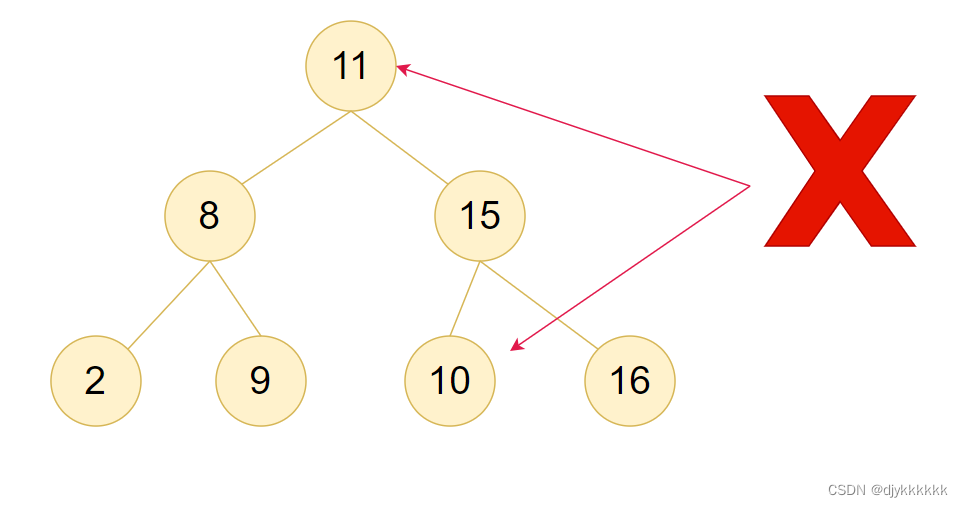
4.平衡二叉搜索树(AVL树):是一种既是平衡二叉树又是二叉搜索树的数据结构。它的每个节点的左子树和右子树的高度差不超过1,并且满足二叉搜索树的性质。
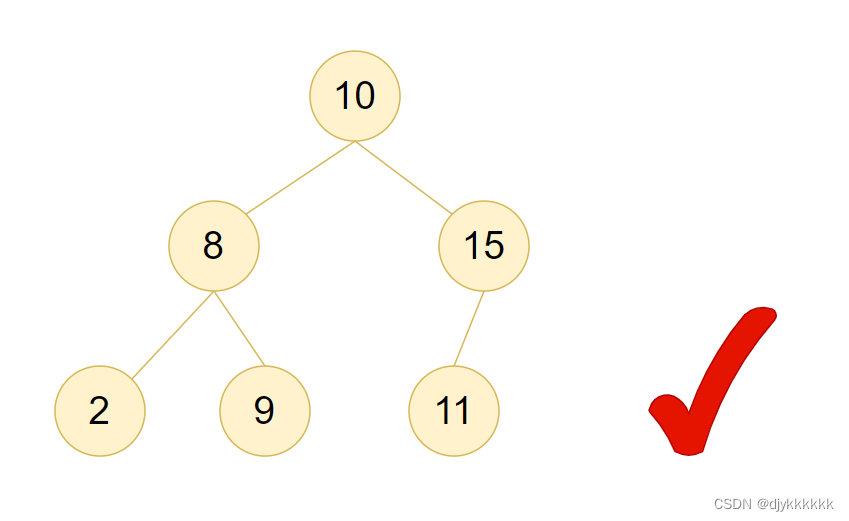
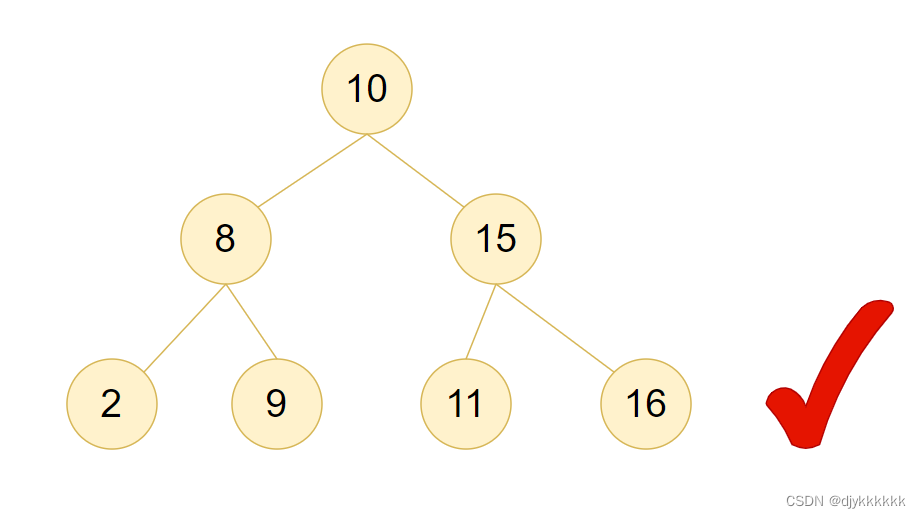

注意:空树是满二叉树、平衡二叉树、二叉搜索树、平衡二叉搜索树的特例。
二.二叉树的存储方式
1.链式存储
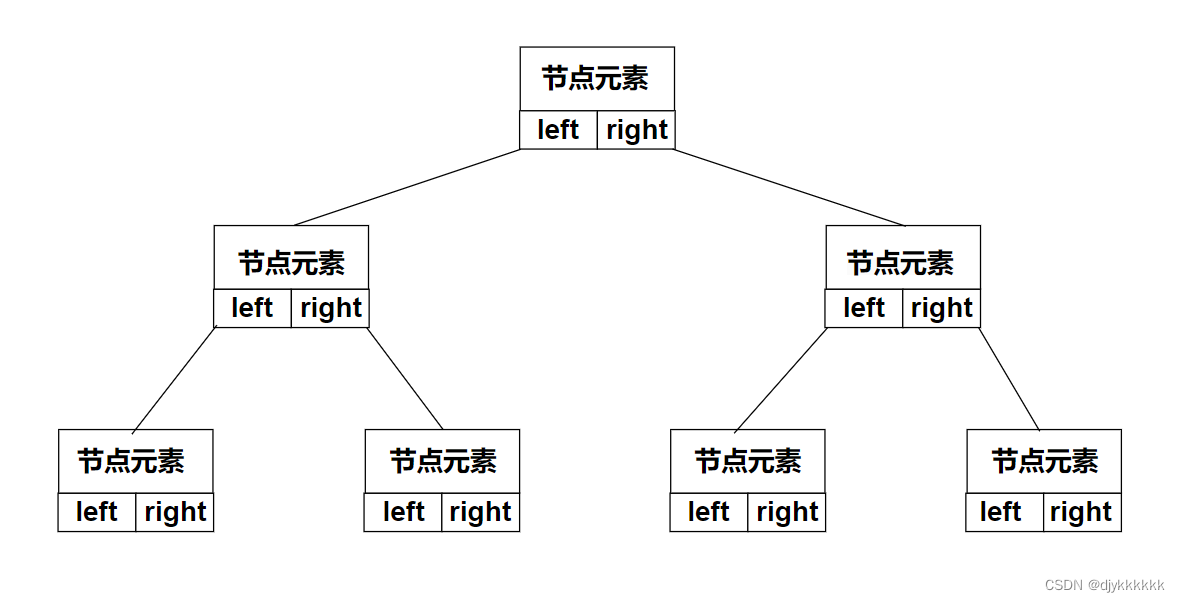
2.数组存储


三.二叉树的遍历方式
1.深度优先遍历
前序遍历(中左右)
中序遍历(左中右)
后序遍历(左右中)
2.广度优先遍历
层序遍历(队列)
四.二叉树的定义
struct TreeNode{
int val;
TreeNode*left;
TreeNode*right;
TreeNode(){
val=0;
left=nullptr;
right=nullptr;
}
TreeNode(int _val){
val=_val;
left=nullptr;
right=nullptr;
}
}
五.总结
- 1.涉及二叉树的问题,首先仔细审题,判断遍历顺序
- 2.其次根据思路写出伪代码
- 3.根据伪代码进行修改