给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

解题思路：回溯+剪枝

 

 

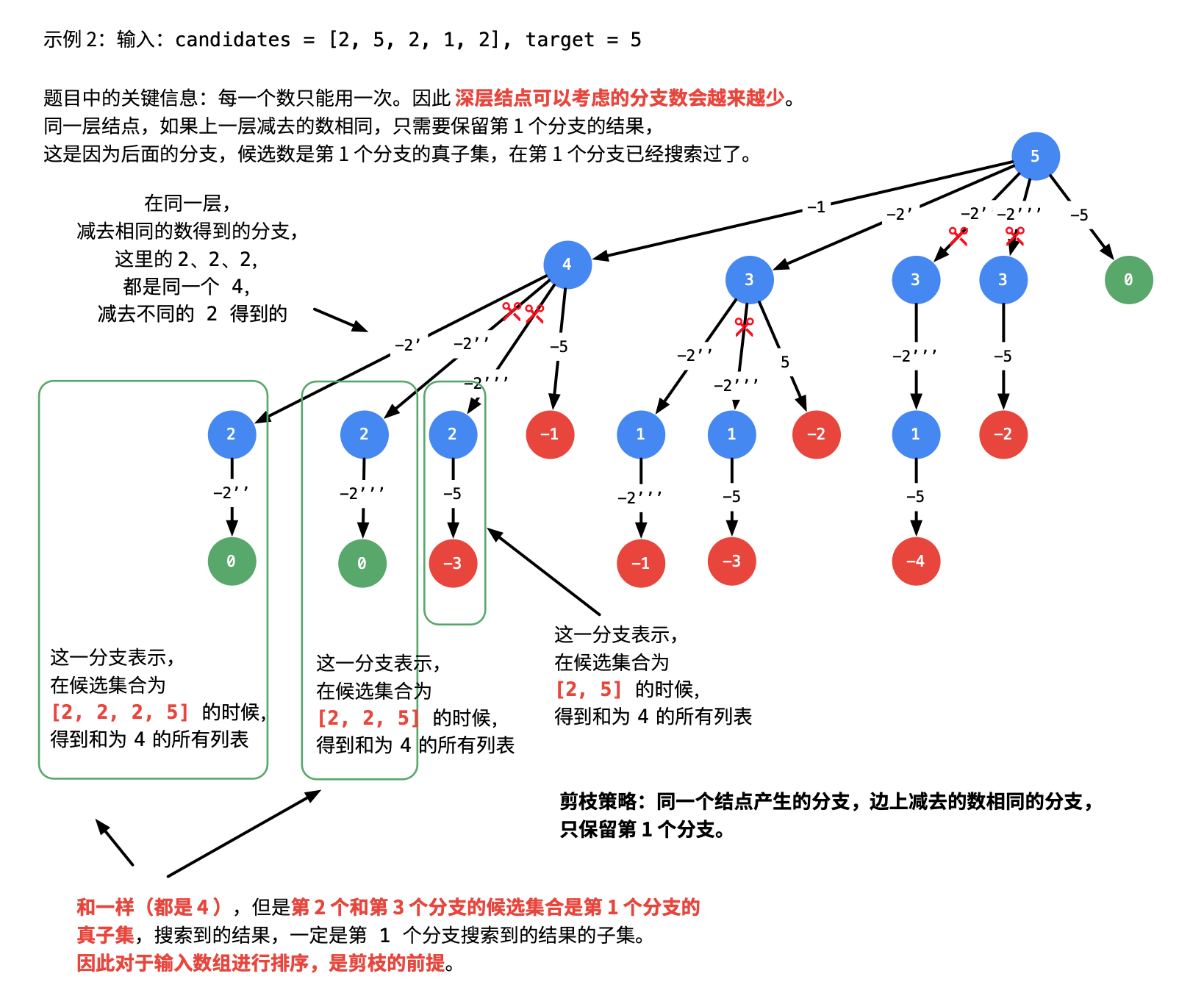
代码：

class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        if(candidates.length == 0){
            return res;
        }
        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates,0,target,path,res);
        return res;
    }
    private void dfs(int[] candidates, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
        if(target == 0){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i = begin; i < candidates.length;i++){
            if(target - candidates[i] < 0){
                break;
            }
            if(i > begin && candidates[i] == candidates[i-1]){
                continue;
            }
            path.addLast(candidates[i]);
            System.out.println("递归之前 => " + path + "，剩余 = " + (target - candidates[i]));
            dfs(candidates,i+1,target - candidates[i],path,res);
            path.removeLast();
             System.out.println("递归之后 => " + path + "，剩余 = " + (target - candidates[i]));
        }
    }
}

 

 [1,1,2,5,6,7,10]

递归之前 => [1]，剩余 = 7
递归之前 => [1, 1]，剩余 = 6
递归之前 => [1, 1, 2]，剩余 = 4
递归之后 => [1, 1]，剩余 = 4
递归之前 => [1, 1, 5]，剩余 = 1
递归之后 => [1, 1]，剩余 = 1
递归之前 => [1, 1, 6]，剩余 = 0
递归之后 => [1, 1]，剩余 = 0
递归之后 => [1]，剩余 = 6
递归之前 => [1, 2]，剩余 = 5
递归之前 => [1, 2, 5]，剩余 = 0
递归之后 => [1, 2]，剩余 = 0
递归之后 => [1]，剩余 = 5
递归之前 => [1, 5]，剩余 = 2
递归之后 => [1]，剩余 = 2
递归之前 => [1, 6]，剩余 = 1
递归之后 => [1]，剩余 = 1
递归之前 => [1, 7]，剩余 = 0
递归之后 => [1]，剩余 = 0
递归之后 => []，剩余 = 7
递归之前 => [2]，剩余 = 6
递归之前 => [2, 5]，剩余 = 1
递归之后 => [2]，剩余 = 1
递归之前 => [2, 6]，剩余 = 0
递归之后 => [2]，剩余 = 0
递归之后 => []，剩余 = 6
递归之前 => [5]，剩余 = 3
递归之后 => []，剩余 = 3
递归之前 => [6]，剩余 = 2
递归之后 => []，剩余 = 2
递归之前 => [7]，剩余 = 1
递归之后 => []，剩余 = 1
输出 => [[1, 1, 6], [1, 2, 5], [1, 7], [2, 6]]