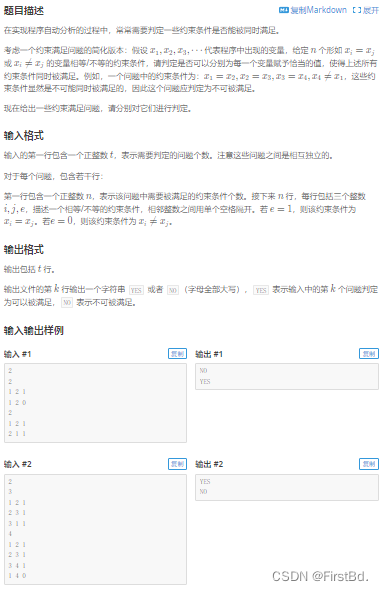
题目

在这里插入图片描述

思路

第一眼：非常简单的并查集

看看标签
在这里插入图片描述
6
为什么离散化会WA+RE呢
首先，并查集是根据f数组来联系两点的，类似于f[x]=y，但是在这个题中我们不能确定x是否为非负整数，而且x过大也会炸内存
那就加一个离散化吧

输入所有元素
排序
去重
把每个元素标号
对标号后的元素进行操作

这样就能保证x为整数且最大为元素的个数了
理论存在，时间开始

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e7+5;
int n,tot;
int f[maxn*2],a[maxn*2];
struct q{
	int x1,x2,if_case;
}qry[maxn];
struct cmp{
	bool operator () (const q& a,const q& b){
		return a.if_case>b.if_case;
	}
};
istream& operator >> (istream& in,q& qr){
	in>>qr.x1>>qr.x2>>qr.if_case;
	return in;
}
void init(int n) { for(int i=0;i<=n;i++) f[i]=i; }
int find(int x) { return f[x]==x?x:f[x]=find(f[x]); }
bool query(int x,int y) { return find(x)==find(y); }
void merge(int x,int y) { f[find(x)]=find(y); }
void read(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>qry[i],a[++tot]=qry[i].x1,a[++tot]=qry[i].x2;//输入每个元素
}
void solve(){
	sort(a+1,a+1+tot);//排序元素
	int res=unique(a+1,a+1+tot)-(a+1);//去重
	for(int i=1;i<=n;i++) qry[i].x1=lower_bound(a+1,a+1+res,qry[i].x1)-(a+1),qry[i].x2=lower_bound(a+1,a+1+res,qry[i].x2)-(a+1);//查找标号，更改元素
	sort(qry+1,qry+1+n,cmp());//先处理1
	init(res);//一定要初始化！
	for(int i=1;i<=n;i++){
		int x1=qry[i].x1,x2=qry[i].x2;
		switch (qry[i].if_case){
			case 1:if(!query(x1,x2)) merge(x1,x2); break;//合并
			case 0:if(query(x1,x2)) { cout<<"NO"<<endl;return; } break;
		}
	}
	cout<<"YES"<<endl;
}
signed main()
{
	int t;cin>>t;
	while(t--) read(),solve();
	return 0;
}