VGG Loss 的基础概念

VGG Loss 是content Loss中的一种。

为了评价图像的perceptual quality，《Perceptual losses for real time style transfer and super-resolution》和《GeneratingImageswithPerceptualSimilarityMetricsbasedonDeepNetworks》将content loss引入到SR中。

Content Loss利用预先训练的图像分类网络来度量图像之间的语义差异。将该网络表示为 $φ$ ，提取的第 $l$ 层high-level representation为 $φ^{(l)}(I)$ ，Content Loss表示为两幅图像high-level representation之间的欧氏距离，如下:
$\mathcal{L}_{\text {content }}(\hat{I}, I ; \phi, l)=\frac{1}{h_l w_l c_l} \sqrt{\sum_{i, j, k}\left(\phi_{i, j, k}^{(l)}(\hat{I})-\phi_{i, j, k}^{(l)}(I)\right)^2},$
其中 $h_l$ 、 $w_l$ 和 $c_l$ 分别为 $l$ 层上表示的高度、宽度和通道数。
Content Loss 本质上是将learned knowledge of hierarchical image features从分类网络 $φ$ 转移到SR网络中。
与像素损失相比，内容损失促使输出图像 $\hat I$ 在感知上与目标图像 $I$ 相似，而不是强迫它们精确匹配像素。因此，它产生的结果在视觉上更加直观，其中VGG和ResNet是最常用的预训练CNN。

VGG 的网络结构

VGG的论文：《Very deep convolutional networks for large-scale image recognition》

VGG网络采用重复堆叠的小卷积核替代大卷积核，在保证具有相同感受野的条件下，提升了网络的深度，从而提升网络特征提取的能力。
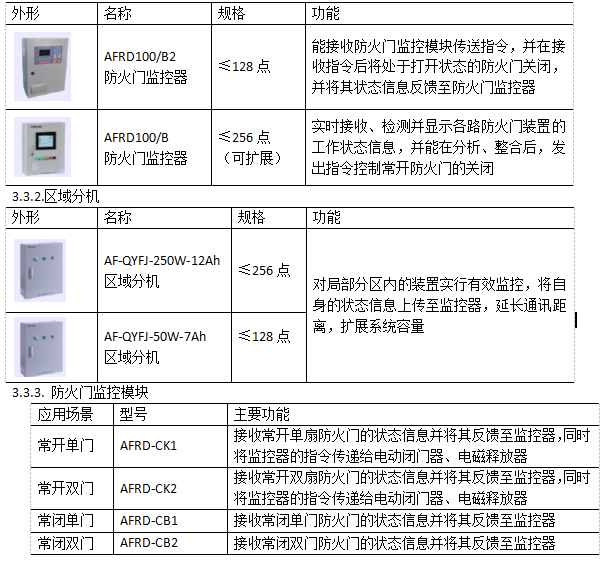
可以把VGG网络看成是数个vgg_block的堆叠，每个vgg_block由几个卷积层+ReLU层，最后加上一层池化层组成。VGG网络名称后面的数字表示整个网络中包含参数层的数量（卷积层或全连接层，不含池化层），如图所示。

在这里插入图片描述

VGG16
5个VGG块的卷积层数量分别为(2, 2, 3, 3, 3)，再加上3个全连接层，总的参数层数量为16，因此命名为VGG16。
VGG19
5个VGG块的卷积层数量分别为(2, 2, 4, 4, 4)，再加上3个全连接层，总的参数层数量为19，因此命名为VGG19。

VGG LOSS 的代码解析

VGG19的代码实现

class VGG19(torch.nn.Module): # VGG19的网络
    def __init__(self, requires_grad=False):
        super().__init__()
        vgg_pretrained_features = torchvision.models.vgg19(pretrained=True).features
        self.slice1 = torch.nn.Sequential()
        self.slice2 = torch.nn.Sequential()
        self.slice3 = torch.nn.Sequential()
        self.slice4 = torch.nn.Sequential()
        self.slice5 = torch.nn.Sequential()
        for x in range(2):
            self.slice1.add_module(str(x), vgg_pretrained_features[x])
        for x in range(2, 7):
            self.slice2.add_module(str(x), vgg_pretrained_features[x])
        for x in range(7, 12):
            self.slice3.add_module(str(x), vgg_pretrained_features[x])
        for x in range(12, 21):
            self.slice4.add_module(str(x), vgg_pretrained_features[x])
        for x in range(21, 30):
            self.slice5.add_module(str(x), vgg_pretrained_features[x])
        if not requires_grad:
            for param in self.parameters():
                param.requires_grad = False

    def forward(self, X):
        h_relu1 = self.slice1(X)
        h_relu2 = self.slice2(h_relu1)
        h_relu3 = self.slice3(h_relu2)
        h_relu4 = self.slice4(h_relu3)
        h_relu5 = self.slice5(h_relu4)
        out = [h_relu1, h_relu2, h_relu3, h_relu4, h_relu5]
        return out

首先我们先打印出vgg_pretrained_features，对应着VGG19中的各个网络层。
在这里插入图片描述

然后分别打印出sclie1,sclie2,sclie3,sclie4, sclie5。可以看出就是把VGG网络的前30层拆分成不同的分组。
在这里插入图片描述

VGG LOSS的代码实现
上文定义的vgg的输出分别是5个sclice输出组成的列表。
假设输入分别是x和y，vgg loss 的值就是分别将x和y将5个sclice输出计算loss，一共有5个loss。然后再将这5个loss按照一定的权重加权求和得到最终的loss 。

# VGG 特征距离损失
class VGGLoss(nn.Module):
    def __init__(self):
        super(VGGLoss, self).__init__()
        self.vgg = VGG19().cuda()
        # self.criterion = nn.L1Loss()
        self.criterion = nn.L1Loss(reduction='sum') # 求和
        self.criterion2 = nn.L1Loss()# 求平均
        self.weights = [1.0 / 32, 1.0 / 16, 1.0 / 8, 1.0 / 4, 1.0] # 各个slice的输出权重

    def forward(self, x, y):
        x_vgg, y_vgg = self.vgg(x), self.vgg(y)
        loss = 0
        for i in range(len(x_vgg)):
            # print(x_vgg[i].shape, y_vgg[i].shape)
            loss += self.weights[i] * self.criterion(x_vgg[i], y_vgg[i].detach()) # 不同slice的loss的加权和
        return loss

    def forward2(self, x, y):
        x_vgg, y_vgg = self.vgg(x), self.vgg(y)
        loss = 0
        for i in range(len(x_vgg)):
            # print(x_vgg[i].shape, y_vgg[i].shape)
            loss += self.weights[i] * self.criterion2(x_vgg[i], y_vgg[i].detach())
        return loss