在七月算法报的班,老师讲的蛮好。好记性不如烂笔头,关键内容还是记录一下吧,课程入口,感兴趣的同学可以学习一下。
-------------------------------------------------------------------------------------------------------------------------------
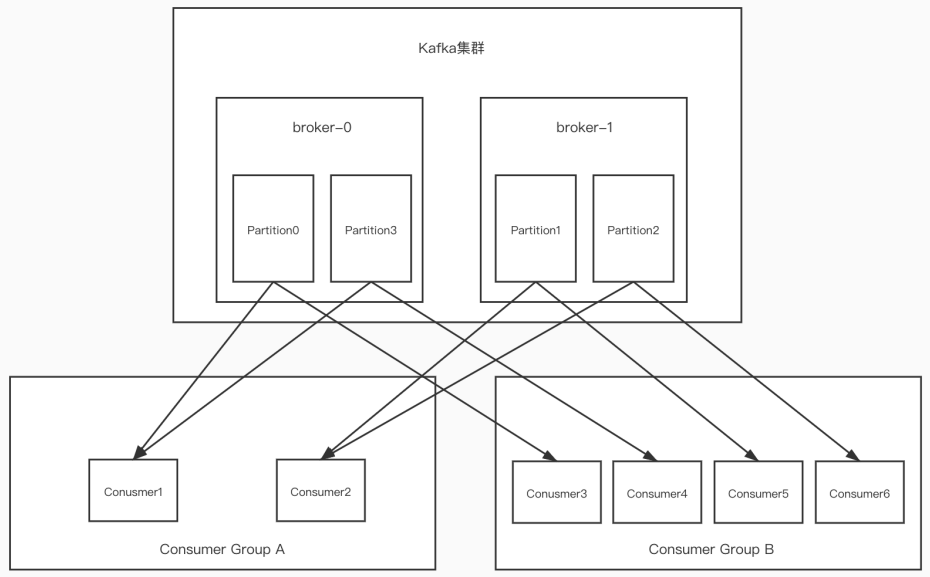
SLAM中的两个关键模型,运动模型与观测模型
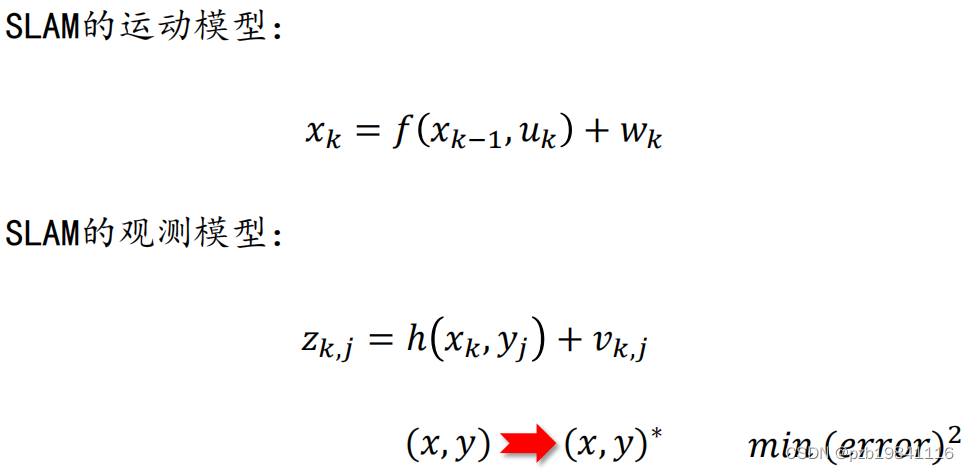
求解有两种方法:批量法与递归法
批量法:一次性给定所有的数据,以此估计所有的变量。
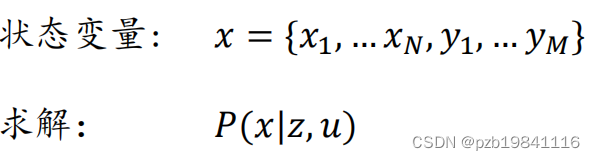
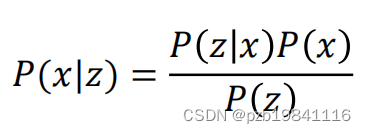

频率学派与贝叶斯学派的区别

贝叶斯学派的做法

最大似然估计的计算方法
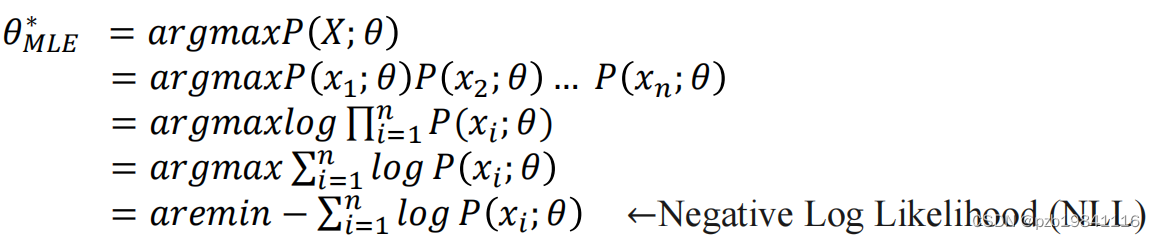
最大后验估计的计算方法
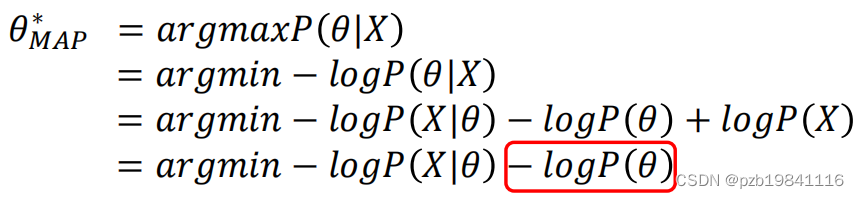
SLAM中最大似然估计与最小二乘法的关系
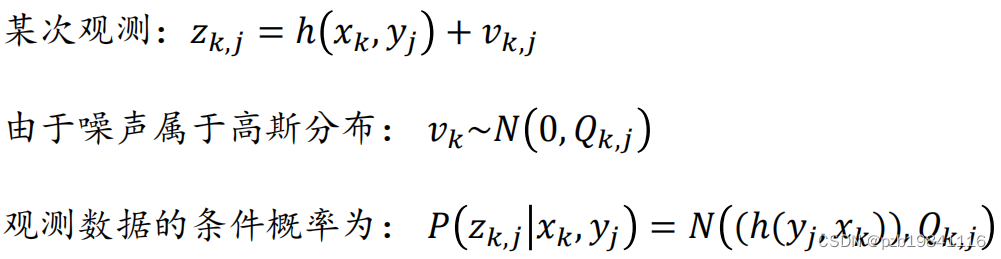



最小二乘法。
首先是用平方和来衡量设计的模型与实际数据之间的差异。
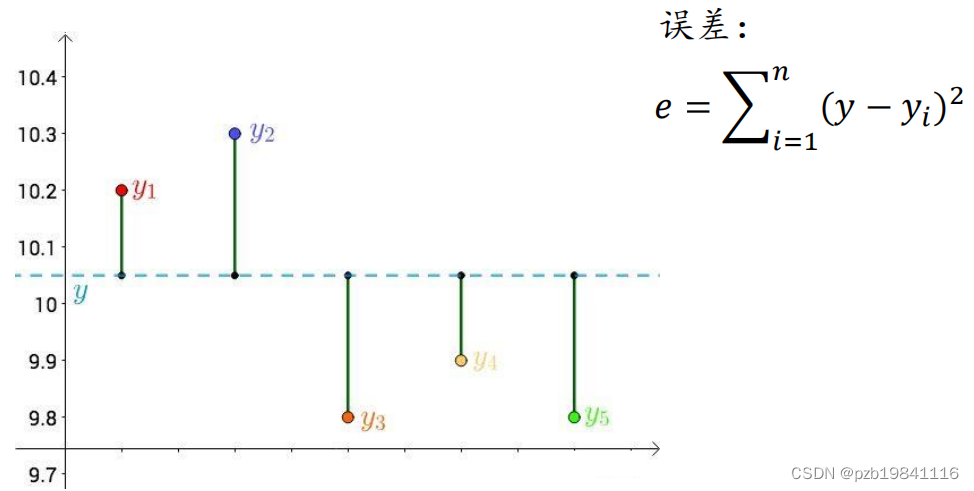
最小二乘就是让这个误差最小
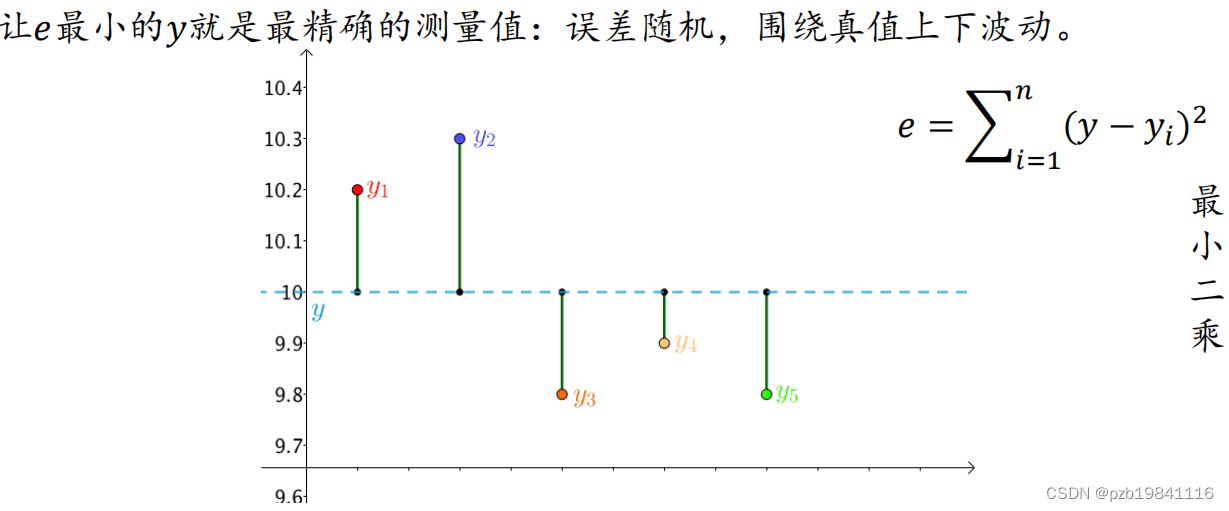
通过计算目标函数的一阶导数,可以找到极值点和鞍点。

迭代法的步骤

求解增量的方法

只保留一阶导数,是梯度下降法

保留二阶导数,是牛顿法

海森矩阵计算量较大,有两种改进方式:Gauss-Newton 和 Levenberg-Marquadt法。
牛顿法与高斯牛顿法的区别在增量方程
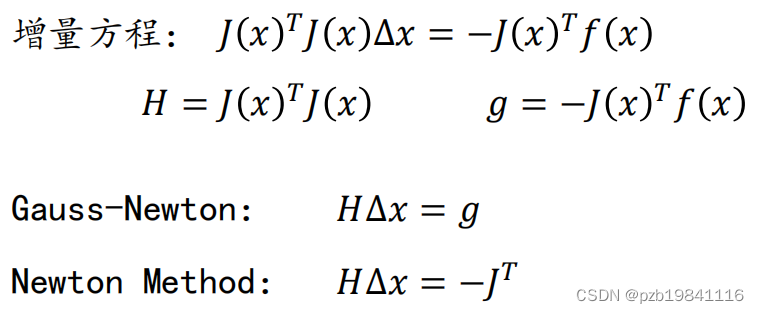
高斯牛顿法的流程:

L-M方法:
高斯牛顿法的弊端是不一定可逆
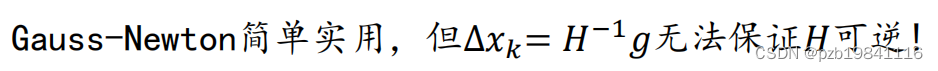
L-M法与高斯牛顿法的区别

L-M法的流程

L-M法的增量方程

图优化理论
所谓的图优化,就是把一个常规的优化问题,以图(Graph)的形式来表述。
比如机器人在空间中移动,并观察几个路标的,可以简化出一个图。
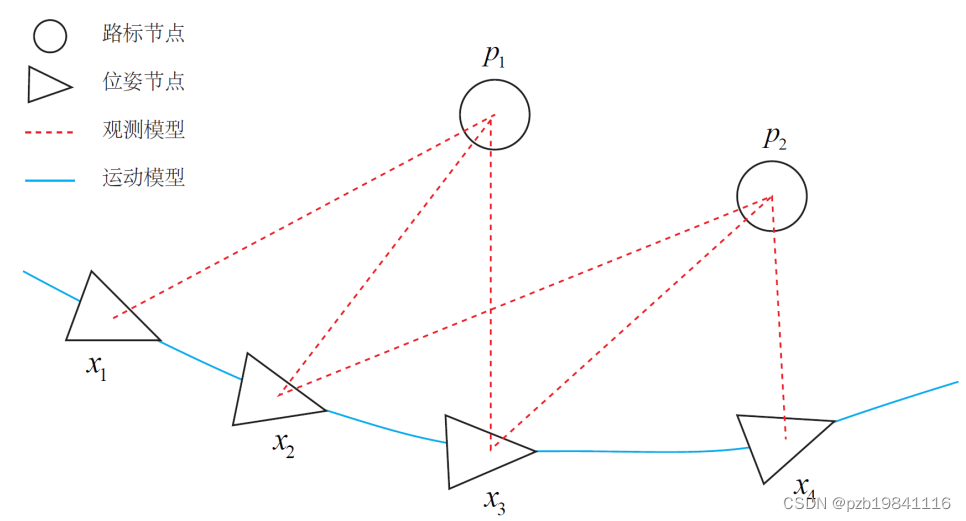
优化的目的就是拟合出最理想的轨迹。
图优化的作用就是将其抽象成一个图结构,用图的形式描述这个问题
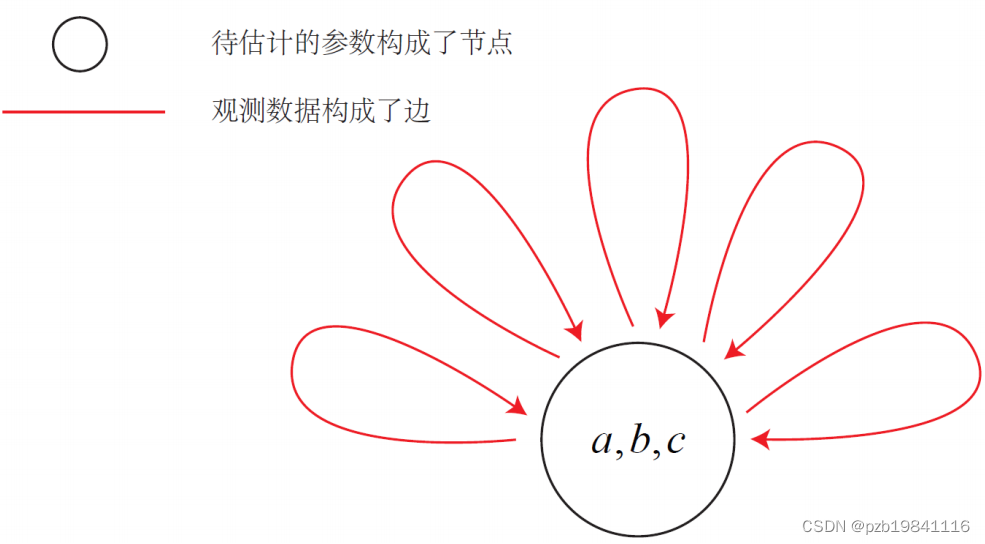
计算过程是:
1.定义顶点和边的类型;
2.构件图;
3.选择优化算法;
4.利用给g2o进行优化,得出结果