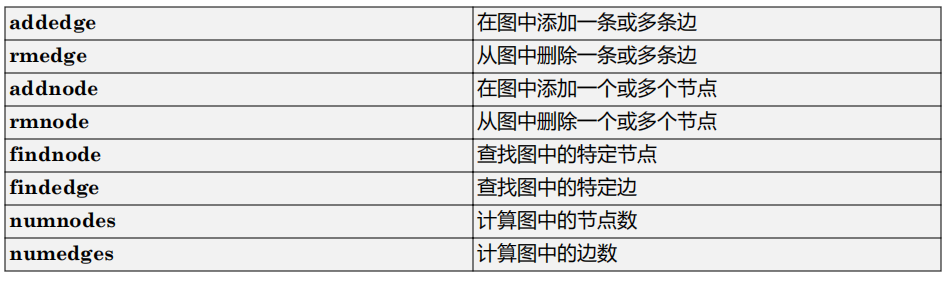
1.有向图和无向图
1.1什么是图?
图是表示各种关系的节点和边的集合:
• 节点
是与对象对应的顶点。
• 边
是对象之间的连接。
• 图的边有时会有权重
,表示节点之间的每个连接的强度(或一些其他属性)。
这些定义是概括性的,因为节点和边在图中的确切含义取决于具体的应用情形。例如,您可以使用图为社交网站中的朋友关系建模。图节点表示人,边表示朋友关系。图与物理对象和各种情况的自然对应关系意味着,您可以使用图对各种系统进行建模。例如:
• 网页链接 - 图节点代表网页,边表示网页之间的超链接。
• 机场 - 图节点代表机场,边表示机场之间的航班。在 MATLAB 中,graph 和
digraph
函数用于构建表示无向图和有向图的对象。
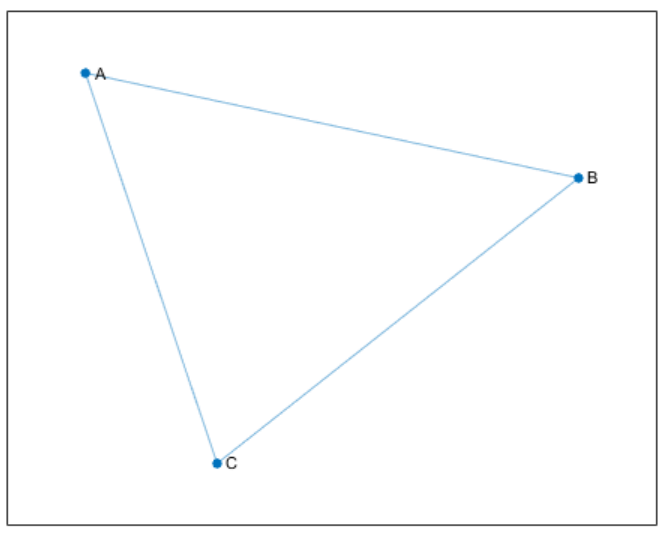
• 无向图的边没有方向。这些边指示双向关系,因为每条边都可以在两个方向上穿过。下图显示了一个包含三个节点和三条边的简单无向图。
• 有向图的边带有方向。这些边指示单向关系,因为每条边只能在单个方向上穿过。下图显示了一个包含三个节点和两条边的简单有向图。
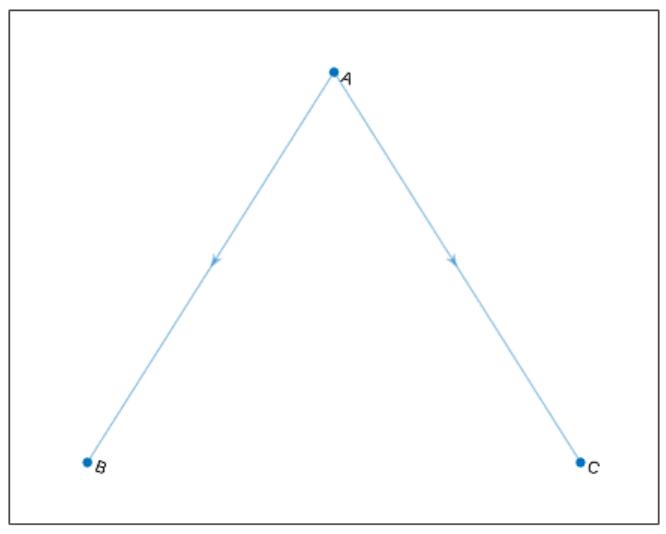
边在图中的确切位置、长度或方向通常没有含义。换言之,只要基础结构不变,就可以通过重新排列节点和/或使边扭曲,以多种不同的方式显示同一个图。
1.2 自环和多重图
使用 graph
和 digraph 创建的图可以有一个或多个自环,自环是指一条边的两端为同一个节点。此外,图可以具有多条有相同源节点和目标节点的边,这样的图称为多重图。多重图可能包含自环,也可能不包含。
对于 MATLAB 中的图算法函数来说,如果图中包含的节点只有一个自环,则不属于多重图。但是,如果图中包含的节点具有多个自环,则属于多重图。
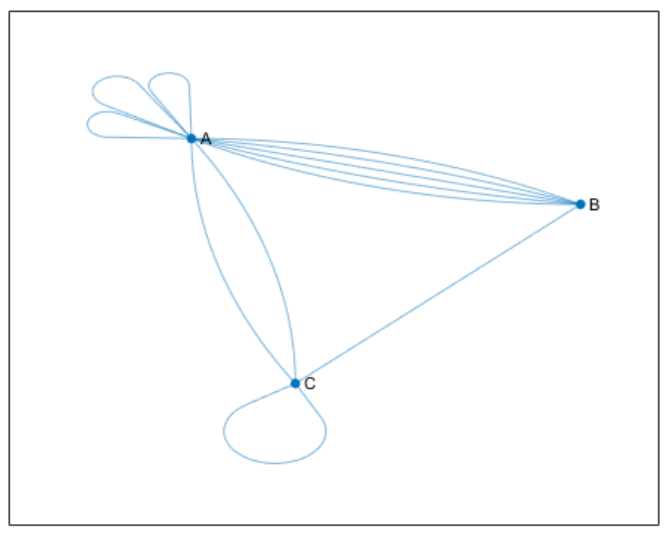
例如,下图显示了具有多个自环的无向多重图。节点 A 有三个自环,节点 C 有一个。该图包含以下三个条件,任何一个条件都满足多重图的条件。
• 节点 A 有三个自环。
• 节点 A 和 B 之间有五条边。
• 节点 A 和 C 之间有两条边。
要确定给定的图是否为多重图,请使用 ismultigraph
函数。
2.创建图
创建图的主要方式包括使用邻接矩阵或边列表。
2.1 邻接矩阵
有一种表示图中信息的方法是使用方形邻接矩阵。邻接矩阵中的非零项表示两个节点之间的边,条目值表示边的权重。邻接矩阵的对角线元素通常为零,但非零对角线元素表示自环或通过边与其自身相连的节点。
• 当您使用 graph 创建无向图时,邻接矩阵必须对称。但在实践中,为避免重复,这些矩阵通常为三角形。要仅使用邻接矩阵的上三角或下三角构建无向图,请使用
graph(A,'upper')
或
graph(A,'lower')
。
• 当您使用 digraph
创建有向图时,邻接矩阵不需要对称。
• 对于大型图,邻接矩阵包含许多零并且通常为稀疏矩阵。
• 您不能从邻接矩阵创建多重图。
例如,考虑创建如下无向图。
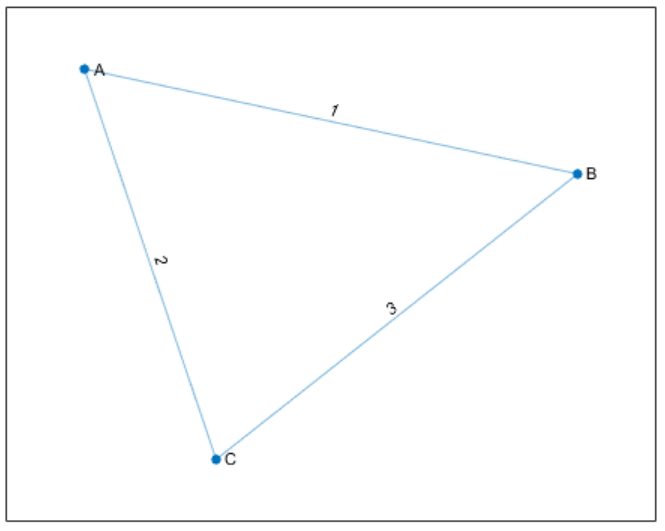
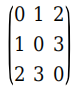
可以通过下面的邻接矩阵表示该图:
要在 MATLAB 中构建该图,请输入:
A = [0 1 2; 1 0 3; 2 3 0];
node_names = {
'A'
,
'B'
,
'C'
};
G = graph(A,node_names)
G =
graph with properties:
Edges: [3×2 table]
Nodes: [3×1 table]
您可以使用邻接矩阵通过 graph
或
digraph
函数来创建图,也可以使用
adjacency 函数求预先存在的图的加权或未加权的稀疏邻接矩阵。
2.2 边列表
表示图信息的另一种方法是列出所有边。例如,考虑创建与上面相同的无向图。现在用边列表来表示该图

从边列表中很容易得出以下结论:该图包含三个唯一节点 A
、B 和 C,这三个节点通过三条列出的边相连。如果该图有断开的节点,边列表中将不会列出这些节点,您需要单独指定它们。 在 MATLAB 中,边列表按列划分为源节点和目标节点。对于有向图,边的方向(从源到目标)很重要;但对于无向图,源节点和目标节点是可以互换的。使用边列表构建该图的一种方法是,对源节点、目标节点和边权重使用单独的输入:
source_nodes = {
'A'
,
'A'
,
'B'
};
target_nodes = {
'B'
,
'C'
,
'C'
};
edge_weights = [1 2 3];
G = graph(source_nodes, target_nodes, edge_weights);
graph 和
digraph
都允许使用边列表构造简单图或多重图。构建图
G
后,可以使用命令
G.Edges 查看边(及其属性)。这些边在 G.Edges 中的顺序首先按源节点(第一列)排列,其次按目标节点(第二列)排列。对于无向图,索引较小的节点列为源节点,索引较大的节点列为目标节点。由于
graph
和
digraph 的底层实现取决于稀疏矩阵,因此许多相同的索引创建成本均适用。使用前述方法之一基于三元对组
(source,target,weight) 一次性构建图比先创建空图再以迭代方式添加更多节点和边要快。为获得最佳性能,请尽量减少对
graph、
digraph、
addedge、
addnode、
rmedge 和
rmnode 的调用次数。
3.图节点 ID
默认情况下,系统会对使用 graph
或 digraph 创建的图的所有节点进行编号。因此,您始终可以通过数值节点索引来引用它们。如果图具有节点名称(即
G.Nodes
包含变量
Name),则您还可以使用节点名称来表示图中的节点。因此,可以通过节点索引或节点名称来表示图中的已命名节点。例如,可以调用节点
1:'A'。术语节点 ID 同时包含节点标识的两个方面的内容。节点 ID 既表示节点索引,也表示节点名称。为方便起见,MATLAB 会记住您在调用大多数图函数时使用的节点 ID 的类型。因此,如果您使用节点索引表示图中的节点,则大多数图函数返回的数值答案也会通过节点索引来表示这些节点。
A = [0 1 1 0; 1 0 1 0; 1 1 0 1; 0 0 1 0];
G = graph(A,{
'a'
,
'b'
,
'c'
,
'd'
});
p = shortestpath(G,1,4)
p =
1 3 4
但是,如果使用节点名称来表示节点,则大多数图函数返回的答案也会通过节点名称来表示这些节点(包含在字符向量元胞数组或字符串数组中)。
p1 = shortestpath(G,
'a'
,
'd'
)
p1 =
1×3 cell array
{'a'} {'c'} {'d'}
使用 findnode 查找给定的节点名称的数值节点 ID。反过来,对于给定的数值节点 ID,请创建指向G.Nodes.Name
的索引以确定对应的节点名称。
4.修改或查询现有图
构造 graph
或
digraph 对象后,您可以使用各种函数来修改图结构或确定图有多少个节点或多少条边。下表列出了一些可用于修改或查询
graph
和
digraph
对象的函数。