【算法题解】53. 计封闭岛屿的数目

news2025/10/31 15:38:10

这是一道 中等难度 的题

https://leetcode.cn/problems/number-of-closed-islands/

题目

二维矩阵 grid 由 $0$ （土地）和 $1$ （水）组成。岛是由最大的 $4$ 个方向连通的 $0$ 组成的群，封闭岛是一个完全由 $1$ 包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

示例 1：

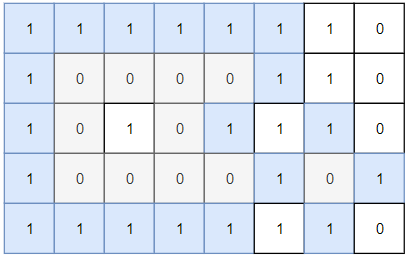
输入：grid =[
    		[1,1,1,1,1,1,1,0],
            [1,0,0,0,0,1,1,0],
            [1,0,1,0,1,1,1,0],
            [1,0,0,0,0,1,0,1],
            [1,1,1,1,1,1,1,0]
		   ] 
输出：2 
解释： 灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

示例 2：

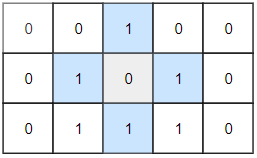
输入：grid = [
    		 [0,0,1,0,0],
    		 [0,1,0,1,0],
    		 [0,1,1,1,0]
			] 
输出：1

示例 3：

输入：grid = [
    		 [1,1,1,1,1,1,1],              
    		 [1,0,0,0,0,0,1],              
             [1,0,1,1,1,0,1],              
             [1,0,1,0,1,0,1],              
             [1,0,1,1,1,0,1],              
             [1,0,0,0,0,0,1],              
             [1,1,1,1,1,1,1]
            ] 
输出：2

提示：

$1 <= g r i d . l e n g t h$ , $g r i d [0] . l e n g t h <= 100$
$0 <= g r i d [i] [j] <= 1$

题解

求岛屿数量也就是求数值为 0 的连通块。思路为遍历二维数组中的每一个元素，如果遇到 0 ，就说明遇到了岛屿，答案计数加一，然后一定要记得将这个岛屿覆盖到的所有 0 设置为 1 或其他 非0 的值，以免导致重复计数。

还有一点需要注意的是，题目要求的是 封闭岛屿，也就是不能包含挨着边界的外部连通块，所以在求内部连通块个数前可以先将外部连通块清除掉，清除方式同样是将所有 0 设置为 1 。

如何将岛屿覆盖到的所有 ‘0’ 设置为 ‘1’ 呢?

首先将当前位置 $g r i d [i] [j]$ 的 0 设置为 1，然后再将挨着这个位置的 上下左右 4个位置的 0 设置为 1，重复此步骤，每一步的处理逻辑都是一样的，又是典型的递归的思路。

递归函数： 将当前位置 $g r i d [i] [j]$ 的 0 设置为 1，然后再递归上下左右4个位置。

边界条件： 有两种可能，分别是：

$i$ 或者 $j$ 出界，返回。
$g r i d [i] [j] = 1$ ，返回。

翻译成代码，以 Java 为例

// 递归函数，i 和 j 为当前位置的坐标
private void resetZero(int[][] grid, int i, int j){

    // 边界条件
    if(i < 0 || i >= grid.length){
        return;
    }
    if(j < 0 || j >= grid[0].length){
        return;
    }
    if(grid[i][j] == 1){
        return;
    }
        
	// 将当前位置设置为1
    grid[i][j] = 1;

    // 递归 上下左右 4个位置
    resetZero(grid, i + 1, j, m, n);
    resetZero(grid, i - 1, j, m, n);
    resetZero(grid, i, j + 1, m, n);
    resetZero(grid, i, j - 1, m, n);
}

综上，总体思路为：

循环遍历 4 条边，遇到 0 就使用递归函数 $rese tZ ero$ 将这个 0 所属于的外部连通块清除掉。
循环遍历 4 条边以内的所有点，遇到 0 就将答案 ans 加一，并将这个 0 所属于的内部连通块清除掉。

Java 代码实现

class Solution {
    public int closedIsland(int[][] grid) {
        // 先把边上的0和其联通的消除掉
        
        int m = grid.length;
        int n = grid[0].length;
        
        for(int i = 0; i < m; i++){
            // i = 0 或者 i = m - 1 或者 j = 0 或者 j = n - 1 时是边
            int step =  i == 0 || i == m - 1 ? 1 : n - 1;
            for(int j = 0; j < n; j += step){
                resetZero(grid, i, j);
            }
        }

        int ans = 0;
        for(int i = 1; i < m - 1; i++){
            for(int j = 1; j < n - 1; j++){
                // 遇到 0，答案就+1；
                // 然后将这个岛清除掉
                if(grid[i][j] == 0){
                    ans++;
                    resetZero(grid, i, j);
                }
            }
        }
        return ans;
    }

    private void resetZero(int[][] grid, int i, int j){

        if(i < 0 || i >= grid.length){
            return;
        }
        if(j < 0 || j >= grid[0].length){
            return;
        }
        if(grid[i][j] == 1){
            return;
        }
        

        grid[i][j] = 1;
        resetZero(grid, i + 1, j);
        resetZero(grid, i - 1, j);
        resetZero(grid, i, j + 1);
        resetZero(grid, i, j - 1);
    }
}

Go 代码实现

func closedIsland(grid [][]int) int {
    m, n := len(grid), len(grid[0])

    for i := 0; i < m; i++ {
        step := 1
        if i != 0 && i != m - 1 {
            step = n - 1
        }
        for j := 0; j < n; j += step {
            resetZero(grid, i, j)
        }
    }

    ans := 0
    for i := 1; i < m - 1; i++ {
        for j := 1; j < n - 1; j++ {
            if grid[i][j] == 0 {
                ans++
            }
            resetZero(grid, i, j)
        }
    }

    return ans
}

func resetZero(grid [][]int, i int, j int) {
    m, n := len(grid), len(grid[0])
    if i < 0 || i >= m || j < 0 || j >= n {
        return
    }
    if grid[i][j] == 1 {
        return
    }

    grid[i][j] = 1

    resetZero(grid, i + 1, j)
    resetZero(grid, i - 1, j)
    resetZero(grid, i, j - 1)
    resetZero(grid, i, j + 1)

}