目录
索引堆及其优化
一、概念及其介绍
二、适用说明
三、结构图示
四、Java 实例代码
src/runoob/heap/IndexMaxHeap.java 文件代码：
索引堆及其优化
一、概念及其介绍
索引堆是对堆这个数据结构的优化。
索引堆使用了一个新的 int 类型的数组，用于存放索引信息。
相较于堆，优点如下：
- 优化了交换元素的消耗。
- 加入的数据位置固定，方便寻找。
二、适用说明
如果堆中存储的元素较大，那么进行交换就要消耗大量的时间，这个时候可以用索引堆的数据结构进行替代，堆中存储的是数组的索引，我们相应操作的是索引。
三、结构图示
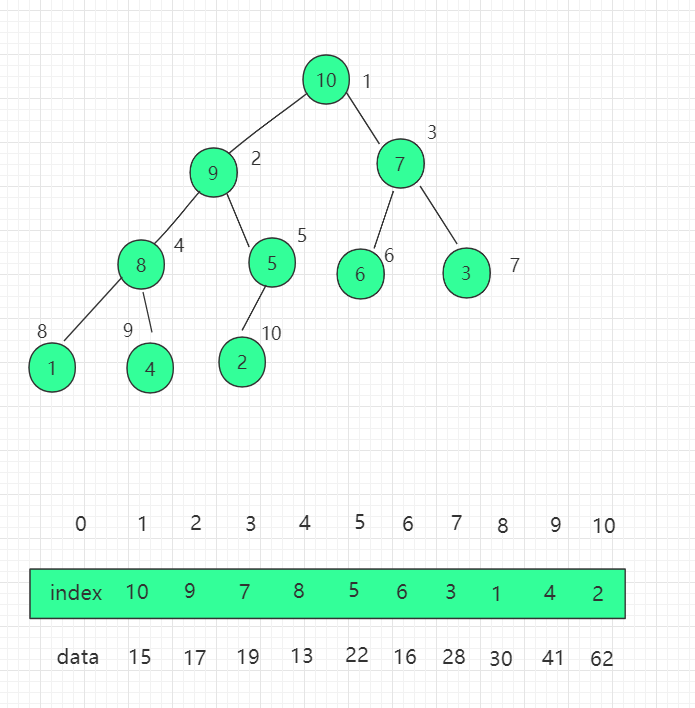
我们需要对之前堆的代码实现进行改造，换成直接操作索引的思维。首先构造函数添加索引数组属性 indexes。
protected T[] data; // 最大索引堆中的数据
protected int[] indexes; // 最大索引堆中的索引
protected int count;
protected int capacity;
相应构造函数调整为，添加初始化索引数组。
...
public IndexMaxHeap(int capacity){
data = (T[])new Comparable[capacity+1];
indexes = new int[capacity+1];
count = 0;
this.capacity = capacity;
}
...
调整插入操作，indexes 数组中添加的元素是真实 data 数组的索引 indexes[count+1] = i。
...
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
public void insert(int i, Item item){
assert count + 1 <= capacity;
assert i + 1 >= 1 && i + 1 <= capacity;
i += 1;
data[i] = item;
indexes[count+1] = i;
count ++;
shiftUp(count);
}
...
调整 shift up 操作：比较的是 data 数组中父节点数据的大小，所以需要表示为 data[index[k/2]] < data[indexs[k]]，交换 index 数组的索引，对 data 数组不产生任何变动，shift down 同理。
...
//k是堆的索引
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
private void shiftUp(int k){
while( k > 1 && data[indexes[k/2]].compareTo(data[indexes[k]]) < 0 ){
swapIndexes(k, k/2);
k /= 2;
}
}
...
从索引堆中取出元素，对大元素为根元素 data[index[1]] 中的数据，然后再交换索引位置进行 shift down 操作。
...
public T extractMax(){
assert count > 0;
T ret = data[indexes[1]];
swapIndexes( 1 , count );
count --;
shiftDown(1);
return ret;
}
...
也可以直接取出最大值的 data 数组索引值
...
// 从最大索引堆中取出堆顶元素的索引
public int extractMaxIndex(){
assert count > 0;
int ret = indexes[1] - 1;
swapIndexes( 1 , count );
count --;
shiftDown(1);
return ret;
}
...
修改索引位置数据
...
// 将最大索引堆中索引为i的元素修改为newItem
public void change( int i , Item newItem ){
i += 1;
data[i] = newItem;
// 找到indexes[j] = i, j表示data[i]在堆中的位置
// 之后shiftUp(j), 再shiftDown(j)
for( int j = 1 ; j <= count ; j ++ )
if( indexes[j] == i ){
shiftUp(j);
shiftDown(j);
return;
}
}
...
四、Java 实例代码
源码包下载：Download
https://www.runoob.com/wp-content/uploads/2020/09/runoob-algorithm-IndexMaxHeap.zip
src/runoob/heap/IndexMaxHeap.java 文件代码：
package runoob.heap;
import java.util.Arrays;
/**
* 索引堆
*/
// 最大索引堆，思路：元素比较的是data数据,元素交换的是索引
public class IndexMaxHeap<T extends Comparable> {
protected T[] data; // 最大索引堆中的数据
protected int[] indexes; // 最大索引堆中的索引
protected int count;
protected int capacity;
// 构造函数, 构造一个空堆, 可容纳capacity个元素
public IndexMaxHeap(int capacity){
data = (T[])new Comparable[capacity+1];
indexes = new int[capacity+1];
count = 0;
this.capacity = capacity;
}
// 返回索引堆中的元素个数
public int size(){
return count;
}
// 返回一个布尔值, 表示索引堆中是否为空
public boolean isEmpty(){
return count == 0;
}
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
public void insert(int i, T item){
assert count + 1 <= capacity;
assert i + 1 >= 1 && i + 1 <= capacity;
i += 1;
data[i] = item;
indexes[count+1] = i;
count ++;
shiftUp(count);
}
// 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
public T extractMax(){
assert count > 0;
T ret = data[indexes[1]];
swapIndexes( 1 , count );
count --;
shiftDown(1);
return ret;
}
// 从最大索引堆中取出堆顶元素的索引
public int extractMaxIndex(){
assert count > 0;
int ret = indexes[1] - 1;
swapIndexes( 1 , count );
count --;
shiftDown(1);
return ret;
}
// 获取最大索引堆中的堆顶元素
public T getMax(){
assert count > 0;
return data[indexes[1]];
}
// 获取最大索引堆中的堆顶元素的索引
public int getMaxIndex(){
assert count > 0;
return indexes[1]-1;
}
// 获取最大索引堆中索引为i的元素
public T getItem( int i ){
assert i + 1 >= 1 && i + 1 <= capacity;
return data[i+1];
}
// 将最大索引堆中索引为i的元素修改为newItem
public void change( int i , T newItem ){
i += 1;
data[i] = newItem;
// 找到indexes[j] = i, j表示data[i]在堆中的位置
// 之后shiftUp(j), 再shiftDown(j)
for( int j = 1 ; j <= count ; j ++ )
if( indexes[j] == i ){
shiftUp(j);
shiftDown(j);
return;
}
}
// 交换索引堆中的索引i和j
private void swapIndexes(int i, int j){
int t = indexes[i];
indexes[i] = indexes[j];
indexes[j] = t;
}
//********************
//* 最大索引堆核心辅助函数
//********************
//k是堆的索引
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
private void shiftUp(int k){
while( k > 1 && data[indexes[k/2]].compareTo(data[indexes[k]]) < 0 ){
swapIndexes(k, k/2);
k /= 2;
}
}
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
private void shiftDown(int k){
while( 2*k <= count ){
int j = 2*k;
if( j+1 <= count && data[indexes[j+1]].compareTo(data[indexes[j]]) > 0 )
j ++;
if( data[indexes[k]].compareTo(data[indexes[j]]) >= 0 )
break;
swapIndexes(k, j);
k = j;
}
}
// 测试 IndexMaxHeap
public static void main(String[] args) {
int N = 1000000;
IndexMaxHeap<Integer> indexMaxHeap = new IndexMaxHeap<Integer>(N);
for( int i = 0 ; i < N ; i ++ )
indexMaxHeap.insert( i , (int)(Math.random()*N) );
}
}
上述修改索引位置在查找索引位置我们使用了遍历，效率不高。我们还可以再优化一遍，维护一组 reverse[i] 数组，表示索引 i 在 indexes(堆) 中的位置，把查找的时间复杂度降为 O(1)。
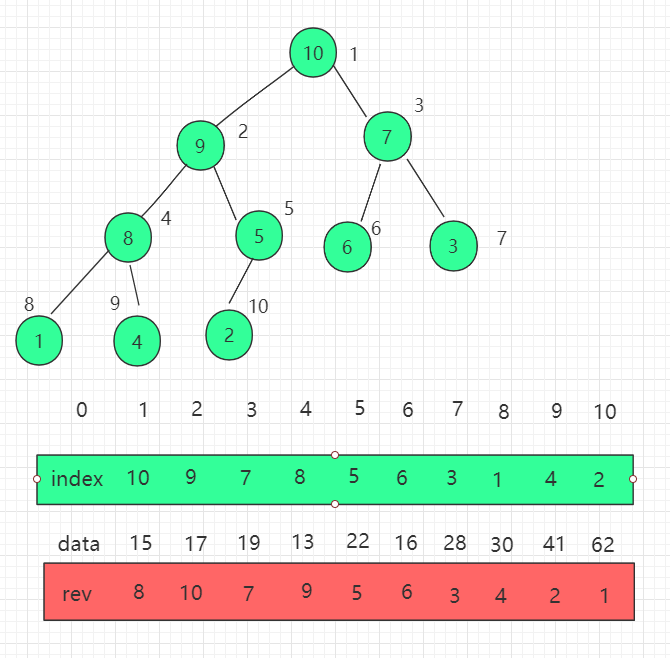
有如下性质：
indexes[i] = j reverse[j] = i indexes[reverse[i]] = i reverse[indexes[i]] = i
