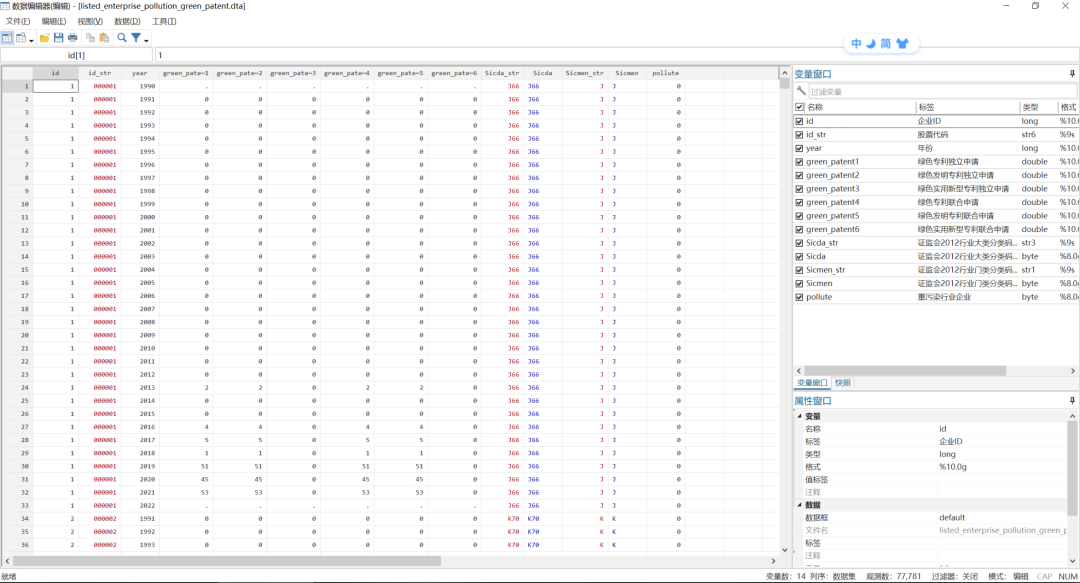
思路：

（1）每个人有一个开心值，并且人物关系呈树形分布。

（2）我们所求为根部人物及其下属的总开心值，显然存在某种递归关系；注意到要求是不能直系父子同时出现，于是考虑树形dp递推，关键在于本元素出现或者不出现，以此利用性质对集合进行划分，构建f[u][0]与f[u][1]分别描述不用u与用u的最佳方案，那么对于f[ufather][0] = max(f[u][0],f[u][1]) + happy[ufather];f[ufather][1] = f[u][0];

（3）最后对f[uzuzong][0]与f[uzuzong][1]取最大即为整体最值。

代码：

#include<bits/stdc++.h>

using namespace std;

const int N = 6e3 + 10;

int st[N],ha[N];
int h[N],e[N],ne[N],idx;
int f[N][2];

void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}

void dfs(int u)
{
    f[u][1] = ha[u];
    
    for(int i = h[u];i != -1;i = ne[i])
    {
        int j = e[i];
        dfs(j);
        
        f[u][1] += f[j][0];
        f[u][0] += max(f[j][1],f[j][0]);
    }
    return;
}

int main()
{
    int n;
    cin >> n;
    for(int i = 1;i <= n;i ++)
        cin >> ha[i];
    
    memset(h,-1,sizeof h);
    for(int i = 1;i <= n - 1;i ++)
    {
        int l,k;
        cin >>l >> k;
        
        add(k,l);
        st[l] = 1; 
    }
    
    int fa;
    for(int i = 1;i <= n;i ++)
        if(st[i] == 0)
        {
           fa = i;
           break;
        }
    
    dfs(fa);
    
    cout << max(f[fa][0],f[fa][1]);
    
    return 0;
}