一、题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例1：

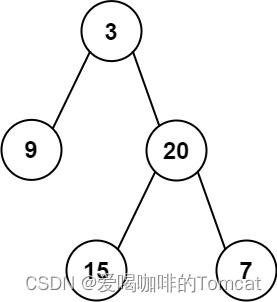
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例2：

输入: preorder = [-1], inorder = [-1]
输出: [-1]

二、代码思路

中序遍历是左根右，前序遍历是根左右，以下面为例：

前序：[1,2,3,4] ---------------- 中序： [2,1,3,4]

前序的第一个元素 1 为根节点，找到根节点在中序遍历中的位置就是中序中的位置1，然后我们就能把中序遍历序列分成两半。2 与 3 4，这代表左右两棵子树的中序遍历序列。同理，我们也能找到2 与 3 4，这里代表左右两棵子树的先序遍历序列。

由于树是一种递归的数据机构，所以针对子树，我们通过其中序序列与前序序列也能推断出其数据结构。

语言描述不够生动，结合代码理解，不过总结来说就是两点：

• 通过树的前序遍历和中序遍历能确定一棵树。
• 树的数据结构是递归的，所以我们找到子树的前序序列和中序序列便可以确定子树，如此我们递归确定即可。

三、代码题解

package leetcode.lc20221213;

import java.util.HashMap;

/*
 * @author lzy
 * @version 1.0
 * */
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

public class Solution01 {
    private HashMap<Integer, Integer> map;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        //边界值处理
        if (preorder.length == 0) {
            return null;
        }
        map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        int n = inorder.length;
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }

    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preLeft, int preRight, int inLeft, int inRight) {
        //递归退出条件
        if (preLeft == preRight) {
            return new TreeNode(preorder[preLeft]);
        }
        //针对1 2  | 2 1 的情况
        //假如右子树为空的情况，此时会出现left > right的现象
        if (preLeft > preRight) {
            return null;
        }
        //前序遍历的第一个节点就是根节点
        TreeNode root = new TreeNode(preorder[preLeft]);
        //从中序遍历中找出左子树的长度
        //拿到根节点在中序遍历的索引
        int rootIndex = this.map.get(preorder[preLeft]);
        int leftLength = rootIndex - inLeft;
        //从中序遍历中找出右子树的长度
        int rightLength = inRight - rootIndex;
        //获取新的左子树的前序遍历左右边界
        //1 2 3 4 前
        //2 1 3 4 中
        //1为根 2为新的左子树，在中序遍历中左子树的范围是 preL + 1， preL + leftLength
        int newPreLeft = preLeft + 1;
        int newPreRight = preLeft + leftLength;
        int newInleft = inLeft;
        int newInRight = rootIndex - 1;
        root.left = myBuildTree(preorder, inorder, newPreLeft, newPreRight, newInleft, newInRight);
        //拿到右子树的中序遍历与先序遍历的左右边界
        newInleft = rootIndex + 1;
        newInRight = inRight;
        newPreLeft = preLeft + leftLength + 1;
        newPreRight = preLeft + leftLength + rightLength;
        root.right = myBuildTree(preorder, inorder, newPreLeft, newPreRight, newInleft, newInRight);
        return root;
    }
}