目录
双向循环链表
力扣 426. 将二叉搜索树转化为排序的双向链表
十字交叉双向循环链表(dancing links)
精确覆盖问题
dancing links
X算法(V1递归版)
POJ 3740 Easy Finding
数独
X算法优化
X算法(V2非递归版)
X算法(V3非递归版)
X算法(V4递归版)
X算法(V5非递归版)
X算法加速(V6非递归版)
X算法(V7基于尾递归的非递归版)
X算法(V8最终版)
X算法应用
拼接覆盖问题
二维非重复块拼接覆盖
三维重复块拼接覆盖
匹配问题
对称之美
分组数字搜索算法
标准数独
不规则数独
分组定和数字搜索算法
满覆盖杀手数独
非满覆盖杀手数独
双向循环链表
力扣 426. 将二叉搜索树转化为排序的双向链表
将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。
对于双向循环列表,你可以将左右孩子指针作为双向循环链表的前驱和后继指针,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
特别地,我们希望可以 就地 完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。
示例 1:
输入:root = [4,2,5,1,3]

输出:[1,2,3,4,5]
解释:下图显示了转化后的二叉搜索树,实线表示后继关系,虚线表示前驱关系。

示例 2:
输入:root = [2,1,3]
输出:[1,2,3]
示例 3:
输入:root = []
输出:[]
解释:输入是空树,所以输出也是空链表。
示例 4:
输入:root = [1]
输出:[1]
提示:
-1000 <= Node.val <= 1000
Node.left.val < Node.val < Node.right.val
Node.val 的所有值都是独一无二的
0 <= Number of Nodes <= 2000
//创建单节点双向循环链表
Node* getList(int val = 0)
{
Node* p = new Node;
p->left = p, p->right = p, p->val = val;
return p;
}
//合并双向循环链表
void merge2list(Node* p1, Node* p2)
{
if (!p1 || !p2)return;
p1->left->right = p2, p2->left->right = p1;
Node* tmp = p2->left;
p2->left = p1->left;
p1->left = tmp;
}
class Solution {
public:
Node* treeToDoublyList(Node* root) {
if (!root)return NULL;
Node* n1 = getList(root->val);
if (root->left) {
Node* n2 = treeToDoublyList(root->left);
merge2list(n2, n1);
n1 = n2;
}
if (root->right) {
Node* n3 = treeToDoublyList(root->right);
merge2list(n1, n3);
}
return n1;
}
};十字交叉双向循环链表(dancing links)
dancing links是双向循环链表的拓展,用于高效解决精确覆盖问题。
精确覆盖问题
给定一个m行n列的0-1矩阵,选出若干行,使得选出的每2行之间没有在同一列的1,所有选出的1的总数为n。
换句话说就是给定m个数,选出若干个,使得选出的数中每2个的且运算都是0,所有选出的数的或运算结果是2^n-1
X算法就是把0-1矩阵转化成dancing links,基于此进行DFS搜索。
dancing links
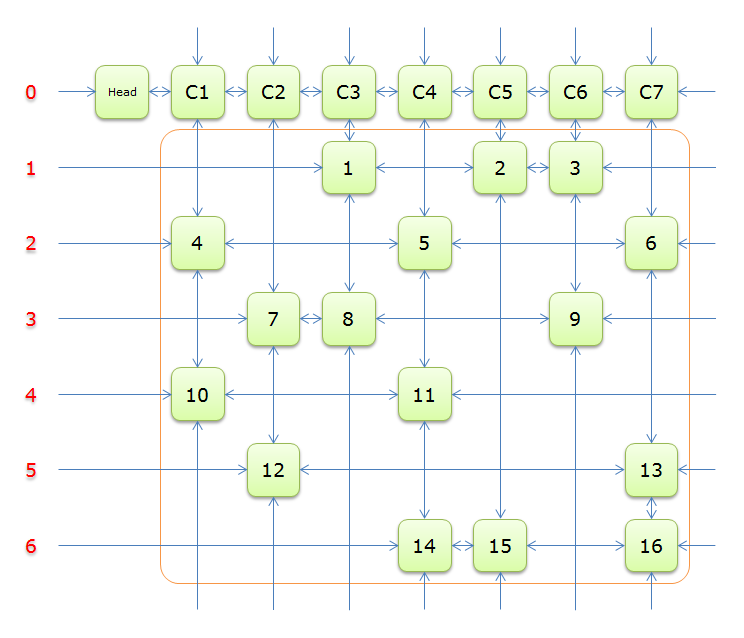
构建一个m+1行n+1列的表格(即把0-1矩阵往上往左拓展一行一列),把所有的1表示成普通节点,忽略0,在第0行添加n+1个特殊节点,编号分别是0到n,其中0号是总head,1到n号是1到n列的列头节点,即空的dancing links有n+1个节点。
从空表开始依次添加节点,动态维护每一列的双向循环列表和每一行的双向循环列表,其中的顺序是任意的(并不像图中看起来这么平齐,即往上往左往下往右各走一步可能不会回到起点,这样实现是为了高效)。
每个节点都记录了它上下左右四个节点的编号,第0行的节点编号是0到n,普通节点的编号是n+1,n+2......
X算法(V1递归版)
从任意一列开始,看这一列哪些行有1,枚举这些行选中哪一行,把选中行的所有1都执行del操作,继续往下搜索,如果没有解就回溯。
递归版实现:
class DancingLink
{
public:
stack<int>rows;
DancingLink(int m, int n, int maxNum)
{
this->m = m, this->n = n;
rhead.resize(m + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i;
}
lef[0] = n, rig[n] = 0;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
}
bool dfs()
{
if (rig[0] == 0)return true;
int c = rig[0];
del(c);
for (int i = down[c]; i != c; i = down[i])
{
for (int j = rig[i]; j != i; j = rig[j])del(col[j]);
rows.push(row[i]);
if (dfs())return true;
rows.pop();
for (int j = rig[i]; j != i; j = rig[j])reback(col[j]);
}
reback(c);
return false;
}
private:
void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j];
}
void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c;
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j;
}
private:
int m, n, key;
vector<int>row, col;//每个节点的行,列
vector<int>rhead;//每行第一个节点的id
vector<int>up, down, lef, rig;//每个节点上下左右的节点id
};m和maxNum只能大不能小,大一些不影响性能。
而n必须完全正确。
POJ 3740 Easy Finding
题目:
Given a M× N matrix A. A ij ∈ {0, 1} (0 ≤ i < M, 0 ≤ j < N), could you find some rows that let every cloumn contains and only contains one 1.
Input
There are multiple cases ended by EOF. Test case up to 500.The first line of input is M, N ( M ≤ 16, N ≤ 300). The next M lines every line contains N integers separated by space.
Output
For each test case, if you could find it output "Yes, I found it", otherwise output "It is impossible" per line.
Sample Input
3 3
0 1 0
0 0 1
1 0 0
4 4
0 0 0 1
1 0 0 0
1 1 0 1
0 1 0 0Sample Output
Yes, I found it
It is impossible单纯的精确覆盖问题。
代码:
#include<iostream>
#include<vector>
#include<stdio.h>
using namespace std;
class DancingLink;
int main()
{
int m, n, x;
while (scanf("%d%d", &m, &n) != EOF)
{
DancingLink s(m, n, 10000);
for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)
{
scanf("%d", &x);
if (x)s.push(i, j);
}
if (s.dfs())printf("Yes, I found it\n");
else printf("It is impossible\n");
}
return 0;
}数独
把数独转化成精确覆盖问题。
依次遍历81个格子,每个格子要么是确定的,要么是9种情况。
对于一个格子有9种情况的,添加9行,对于确定的格子只需要添加1行。
而列一共有81*4列,每一列代表一个校验,一共四种校验类型,分别是:
每个格子只能填1个数(81个格子),每行每个数只能出现一次(9*9=81),每列每个数只能出现一次(9*9=81),每个九宫格每个数只能出现一次(9*9=81)
string Sudoku(string s, char cEmpty = '.')
{
int num = 0;
for (auto c : s)if (c != cEmpty)num++;
int m = (81 - num) * 9 + num;
int n = 81 * 4;
DancingLink d(m, n, m * 4 + n + 5);
int row = 0;
map<int, int>mrow;
mrow[0] = -1;
for (int i = 0; i < 81; i++) {//第i个格子
char c = s[i];
int low = 0, high = 8;
if (c != cEmpty)low = high = c - '1';//第i个格子的搜索值域
for (int x = low; x <= high; x++) {
d.push(++row, i + 1), d.push(row, i / 9 * 9 + x + 81 + 1);
d.push(row, i % 9 * 9 + x + 162 + 1), d.push(row, (i / 27 * 3 + i % 9 / 3) * 9 + x + 243 + 1);
mrow[row] = i;
}
}
if (!d.dfs())return "";
stack<int>rows = d.rows;
string ans = s;
while (!rows.empty()) {
int row = rows.top();
rows.pop();
int id = mrow[row];
if (s[id] == cEmpty) {
ans[id] = '1';
while (mrow[row - 1] == id)ans[id]++, row--;
}
else ans[id] = s[id];
}
return ans;
}测试用例:
#include<cstdlib>
#include<ctime>
using namespace std;
int main()
{
string s = ".2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.";
clock_t start, endd;
start = clock();
cout << Sudoku(s);
endd = clock();
double endtime = (double)(endd - start) / CLOCKS_PER_SEC;
cout << "Total time:" << endtime << endl; //s为单位
return 0;
}输出:
527389416819426735436751829375692184194538267268174593643217958951843672782965341
V1耗时242毫秒,POJ 3074 Sudoku里面的暴力搜索耗时是8毫秒。
X算法优化
X算法(V2非递归版)
废了好大一股劲,改成了非递归版:
class DancingLink
{
public:
stack<int>sc,rows;//覆盖选中的行,值的范围是从1到m
DancingLink(int m, int n, int maxNum)
{
this->m = m, this->n = n;
rhead.resize(m + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i;
}
lef[0] = n, rig[n] = 0;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
}
bool dfs()
{
while (true) {
if (rig[0] == 0)return true;
int c = rig[0];
del(c);
if (c == down[c]) {
reback(c);
if (sc.empty())return false;
c = sc.top();
sc.pop();
rows.pop();
for (int j = rig[c]; j != c; j = rig[j])reback(col[j]);
}
while (true) {
c = down[c];
if (c <= n) {
reback(col[c]);
if (sc.empty())return false;
c = sc.top();
sc.pop();
rows.pop();
for (int j = rig[c]; j != c; j = rig[j])reback(col[j]);
}
else break;
}
sc.push(c);//记录选中id
rows.push(row[c]);
for (int j = rig[c]; j != c; j = rig[j]) {
del(col[j]);
}
}
return false;
}
private:
void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j];
}
void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c;
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j;
}
private:
int m, n, key;
vector<int>row, col;//每个节点的行,列
vector<int>rhead;//每行第一个节点的id
vector<int>up, down, lef, rig;//每个节点上下左右的节点id
};这个dfs函数应该还可以简化,但是先不急着简化,逻辑通俗易懂就行,先确认功能正确再重构。
V2耗时247毫秒
X算法(V3非递归版)
直接根据V1递归版进行修改,把递归调用和回溯分别换成goto
class DancingLink
{
public:
stack<int>sc, si, rows;
DancingLink(int m, int n, int maxNum)
{
this->m = m, this->n = n;
rhead.resize(m + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i;
}
lef[0] = n, rig[n] = 0;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
}
int c, i;
bool dfs()
{
h1:
c = rig[0];
if (c == 0)return true;
del(c);
for (i = down[c]; i != c; i = down[i])
{
for (int j = rig[i]; j != i; j = rig[j])del(col[j]);
sc.push(c), si.push(i), rows.push(row[i]);
goto h1;
h2:
c = sc.top(), i = si.top(), sc.pop(), si.pop(),rows.pop();
for (int j = rig[i]; j != i; j = rig[j])reback(col[j]);
}
reback(c);
if (c != 1)goto h2;
return false;
}
private:
void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j];
}
void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c;
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j;
}
private:
int m, n, key;
vector<int>row, col;//每个节点的行,列
vector<int>rhead;//每行第一个节点的id
vector<int>up, down, lef, rig;//每个节点上下左右的节点id
};V3耗时245毫秒
X算法(V4递归版)
把V1改成reback和del反对称式的写法
class DancingLink
{
public:
DancingLink(int m, int n, int maxNum)
{
this->m = m, this->n = n;
rhead.resize(m + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i;
}
lef[0] = n, rig[n] = 0;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
}
stack<int>rows;//覆盖选中的行,值的范围是从1到m
bool dfs()
{
if (rig[0] == 0)return true;
int c = rig[0];
del(c);
for (int i = down[c]; i != c; i = down[i])
{
for (int j = rig[i]; j != i; j = rig[j])del(col[j]);
rows.push(row[i]);
if (dfs())return true;
rows.pop();
for (int j = lef[i]; j != i; j = lef[j])reback(col[j]);
}
reback(c);
return false;
}
private:
void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j];
}
void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c;
for (int i = up[c]; i != c; i = up[i])
for (int j = lef[i]; j != i; j = lef[j])
down[up[j]] = up[down[j]] = j;
}
private:
int m, n, key;
vector<int>row, col;//每个节点的行,列
vector<int>rhead;//每行第一个节点的id
vector<int>up, down, lef, rig;//每个节点上下左右的节点id
};V4耗时219毫秒
X算法(V5非递归版)
把V2做了简化,同时把输出栈改成输出vector,提前把vector的尺寸设定好,减少入栈出栈操作。
class DancingLink
{
public:
vector<int>sc, rows;//覆盖选中的行,值的范围是从1到m
int scid = 0, rowsid = 0;
DancingLink(int m, int n, int maxNum)
{
this->m = m, this->n = n, maxNum += n + 1;
rhead.resize(m + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
sc.resize(m), rows.resize(m);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i;
}
lef[0] = n, rig[n] = 0;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
}
bool dfs()
{
while (true) {
int c = rig[0];
if (c == 0) {
rows.resize(rowsid);
return true;
}
del(c);
while (c = down[c]) {
if (c > n)break;
reback(col[c]);
c = sc[--scid];
rowsid--;
for (int j = rig[c]; j != c; j = rig[j])reback(col[j]);
}
sc[scid++]=c;//记录选中id
rows[rowsid++]=row[c];
for (int j = rig[c]; j != c; j = rig[j])del(col[j]);
}
return false;
}
private:
inline void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j];
}
inline void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c;
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j;
}
private:
int m, n, key;
vector<int>row, col;//每个节点的行,列
vector<int>rhead;//每行第一个节点的id
vector<int>up, down, lef, rig;//每个节点上下左右的节点id
};
string Sudoku(string s, char cEmpty = '.')
{
int num = 0;
for (int i = 0; i < 81; i++)if (s[i] != cEmpty)num++;
int m = (81 - num) * 9 + num;
int n = 81 * 4;
DancingLink d(m, n, m * 4);
int row = 0;
map<int, int>mrow;
mrow[0] = -1;
for (int i = 0; i < 81; i++) {//第i个格子
char c = s[i];
int low = 0, high = 8;
if (c != cEmpty)low = high = c - '1';//第i个格子的搜索值域
for (int x = low; x <= high; x++) {
d.push(++row, i + 1), d.push(row, i / 9 * 9 + x + 81 + 1);
d.push(row, i % 9 * 9 + x + 162 + 1), d.push(row, (i / 27 * 3 + i % 9 / 3) * 9 + x + 243 + 1);
mrow[row] = i;
}
}
if (!d.dfs())return "";
string ans = s;
for (auto row:d.rows) {
int id = mrow[row];
if (s[id] == cEmpty) {
ans[id] = '1';
while (mrow[row - 1] == id)ans[id]++, row--;
}
else ans[id] = s[id];
}
return ans;
}V5耗时223毫秒
X算法加速(V6非递归版)
搜索最简单有效的加速,就是先从可能性少的开始搜。
我们实时统计每一列的节点个数,删掉的列和第0列都认为是正无穷。
每次不是从rig[0]开始搜,而是从节点最少的那一列开始搜。
class DancingLink
{
public:
vector<int>rows;//覆盖选中的行,值的范围是从1到m
DancingLink(int m, int n, int maxNum)
{
this->m = m, this->n = n, maxNum += n + 1;
rhead.resize(m + 1), nums.resize(n + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
sc.resize(m), rows.resize(m);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i, nums[i] = 0;
}
lef[0] = n, rig[n] = 0, nums[0] = INT_MAX;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
nums[c]++;
}
bool dfs()
{
while (true) {
if (rig[0] == 0) {
rows.resize(rowsid);
return true;
}
int c = min_element(nums.begin(), nums.end()) - nums.begin();
del(c);
while (c = down[c]) {
if (c > n)break;
reback(col[c]);
c = sc[--scid];
rowsid--;
for (int j = rig[c]; j != c; j = rig[j])reback(col[j]);
}
sc[scid++]=c;//记录选中id
rows[rowsid++]=row[c];
for (int j = rig[c]; j != c; j = rig[j])del(col[j]);
}
return false;
}
private:
inline void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j], nums[col[j]]--;
nums[c] = INT_MAX;
}
inline void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c, nums[c] = 0;
for (int i = down[c]; i != c; i = down[i]) {
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j, nums[col[j]]++;
nums[c]++;
}
}
private:
int m, n, key;
vector<int>row, col;//每个节点的行,列
vector<int>rhead;//每行第一个节点的id
vector<int>up, down, lef, rig;//每个节点上下左右的节点id
vector<int>nums;//每一列的元素个数
vector<int>sc;
int scid = 0, rowsid = 0;
};其中nums就是记录每一列的元素个数,用min_element直接找到其中最小值的位置。
V6耗时1毫秒
X算法(V7基于尾递归的非递归版)
坐我后面的同事看了本文之后,把V1递归版变成了尾递归版:
class DancingLink
{
public:
std::stack<int>rows;
DancingLink(int m, int n, int maxNum)
{
this->m = m, this->n = n;
rhead.resize(m + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i;
}
lef[0] = n, rig[n] = 0;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
}
bool dfs()
{
if (rig[0] == 0) return true;
if (opts.empty()) return false;
auto runner = std::move(opts.top());
opts.pop();
runner();
return dfs();
}
void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j];
}
void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c;
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j;
}
auto MakeOpt()->std::function<void()>
{
return [=] {
int c = rig[0];
del(c);
auto cre = [=] {
reback(c);
};
opts.push(std::move(cre));
for (int i = up[c]; i != c; i = up[i]) {
auto subpush = [=] {
for (int j = rig[i]; j != i; j = rig[j])del(col[j]);
rows.push(row[i]);
};
auto subre = [=] {
rows.pop();
for (int j = rig[i]; j != i; j = rig[j]) reback(col[j]);
};
opts.push(std::move(subre));
opts.push(MakeOpt());
opts.push(std::move(subpush));
}
};
}
auto Dfs() {
opts.push(MakeOpt());
return dfs();
}
private:
int m, n, key;
std::vector<int>row, col;//每个节点的行,列
std::vector<int>rhead;//每行第一个节点的id
std::vector<int>up, down, lef, rig;//每个节点上下左右的节点id
std::stack<std::function<void()>> opts;
};这个运行会报栈溢出,因为递归深度太深了。
直接把它改成非递归版:
class DancingLink
{
public:
std::stack<int>rows;
DancingLink(int m, int n, int maxNum)
{
this->m = m, this->n = n;
rhead.resize(m + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i;
}
lef[0] = n, rig[n] = 0;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
}
bool dfs()
{
while (true) {
if (rig[0] == 0) return true;
if (opts.empty()) return false;
auto runner = std::move(opts.top());
opts.pop();
runner();
}
}
void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j];
}
void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c;
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j;
}
auto MakeOpt()->std::function<void()>
{
return [=] {
int c = rig[0];
del(c);
auto cre = [=] {
reback(c);
};
opts.push(std::move(cre));
for (int i = up[c]; i != c; i = up[i]) {
auto subpush = [=] {
for (int j = rig[i]; j != i; j = rig[j])del(col[j]);
rows.push(row[i]);
};
auto subre = [=] {
rows.pop();
for (int j = rig[i]; j != i; j = rig[j]) reback(col[j]);
};
opts.push(std::move(subre));
opts.push(MakeOpt());
opts.push(std::move(subpush));
}
};
}
auto Dfs() {
opts.push(MakeOpt());
return dfs();
}
private:
int m, n, key;
std::vector<int>row, col;//每个节点的行,列
std::vector<int>rhead;//每行第一个节点的id
std::vector<int>up, down, lef, rig;//每个节点上下左右的节点id
std::stack<std::function<void()>> opts;
};V7耗时398毫秒
X算法(V8最终版)
前面几个版本中,V6是性能最高的,我在这个版本的基础上做了微调,使得它既可以求任意一个解,也可以求所有解。
class DancingLink // 精确覆盖算法
{
public:
DancingLink(int m, int n, int maxNum) //01矩阵的行、列、1的最大数量
{
this->m = m, this->n = n, maxNum += n + 1;
rhead.resize(m + 1), nums.resize(n + 1);
row.resize(maxNum), col.resize(maxNum);
up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
sc.resize(m), rows.resize(m);
for (int i = 0; i <= n; i++)
{
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i, nums[i] = 0;
}
lef[0] = n, rig[n] = 0, nums[0] = INT_MAX;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c)//新增坐标在(r,c)的一个节点
{
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else
{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
nums[c]++;
}
vector<vector<int>> getAllAns()
{
return dfs(false);
}
vector<int> getAnyAns()
{
auto v = dfs(true);
if (v.size())return v[0];
return vector<int>{};
}
private:
vector<vector<int>> dfs(bool onlyOne)
{
vector<vector<int>>ans;
while (true) {
if (rig[0] == 0) {
rows.resize(rowsid);
ans.push_back(rows);
rows.resize(m);
if (onlyOne)return ans;
}
int c = min_element(nums.begin() + 1, nums.end()) - nums.begin();
if (rig[0] == 0)c = 0;
del(c);
while (true) {
c = down[c];
if (c > n)break;
reback(col[c]);
if (scid == 0)return ans;
c = sc[--scid];
rowsid--;
for (int j = rig[c]; j != c; j = rig[j])reback(col[j]);
}
sc[scid++] = c;//记录选中id
rows[rowsid++] = row[c];
for (int j = rig[c]; j != c; j = rig[j])del(col[j]);
}
return ans;
}
inline void del(int c)//删除第c列的所有元素和他们所在行的所有元素
{
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j], nums[col[j]]--;
nums[c] = INT_MAX;
}
inline void reback(int c)//完全回退del操作
{
lef[rig[c]] = rig[lef[c]] = c, nums[c] = 0;
for (int i = down[c]; i != c; i = down[i]) {
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j, nums[col[j]]++;
nums[c]++;
}
}
private:
int m, n, key;
vector<int>row, col;//每个节点的行,列
vector<int>rhead;//每行第一个节点的id
vector<int>up, down, lef, rig;//每个节点上下左右的节点id
vector<int>nums;//每一列的元素个数
vector<int>sc;
int scid = 0, rowsid = 0;
vector<int>rows;//覆盖选中的行,值的范围是从1到m
};
X算法应用
拼接覆盖问题
拼接覆盖问题也可以转成精确覆盖问题。
二维非重复块拼接覆盖
只要枚举所有的块,每个块的每一种可能性就是dancing links的一行,待覆盖区域的每个格子就是一列。除此之外,还要限制每个块只能被用1次,这也是对应一列。
PS:如果有2个重复的块,直接当他们是2个不重复的块,也没有问题。
struct Grid
{
int r, c;
Grid(int rr, int cc) :r(rr), c(cc) {}
bool operator<(const Grid& g) const
{
if (r == g.r)return c < g.c;
return r < g.r;
}
};
struct Block //一个块的所有形态
{
vector<vector<Grid>>grids;
Block(vector<vector<Grid>>g, int maxDr, int maxDc, const map<Grid, int>& m)//块的所有形态在最小位置包含的格子,最大偏移,待覆盖区域包含的格子
{
this->m = m;
for (auto& g2 : g) {
for (int i = 0; i < maxDr; i++)for (int j = 0; j < maxDc; j++) {
for (auto& x : g2)x.r += i, x.c += j;
if (inBoard(g2))grids.push_back(g2);
for (auto& x : g2)x.r -= i, x.c -= j;
}
}
}
Block() {}
private:
map<Grid, int>m;
bool inBoard(vector<Grid>& g)
{
for (auto& x : g)if (!m[x])return false;
return true;
}
};
vector<vector<Grid>> Cover(vector<Block>blocks, map<Grid, int>& mg)//所有块,待覆盖区域包含的格子编号为1,2,3...
{
int m = 0, maxNum = 0;
for (auto& block : blocks) {
m += block.grids.size();
maxNum += block.grids.size() * (block.grids[0].size()+1);
}
DancingLink d(m, mg.size() + blocks.size(), maxNum);
int r = 0;
map<int, int>mrow;
for (int i = 0; i < blocks.size(); i++) {
mrow[r + 1] = i + 1;
for (auto& grids : blocks[i].grids) {
++r;
for (auto& g : grids)d.push(r, mg[g]);
d.push(r, i + 1 + mg.size());
}
}
d.dfs();
vector<int> rows = d.rows;
vector<vector<Grid>> ans;
for (auto row : rows) {
int id = 0;
while (!mrow[row])row--, id++;;
ans.push_back(blocks[mrow[row] - 1].grids[id]);
}
return ans;
}应用示例:
日历拼图
三维重复块拼接覆盖
假如部分块是没有数量限制的(从0到正无穷都可以),那么只需要取消“这个块只能被用1次”这个限制对应的列即可,其他的不变。
struct Grid
{
int r, c, h;
Grid(int rr, int cc,int hh) :r(rr), c(cc),h(hh) {}
bool operator<(const Grid& g) const
{
if (h == g.h) {
if (r == g.r)return c < g.c;
return r < g.r;
}
return h < g.h;
}
};
struct Block //一个块的所有形态
{
vector<vector<Grid>>grids;
Block(vector<vector<Grid>>g, int maxDr, int maxDc, int maxDh, const map<Grid, int>& m)//块的所有形态在最小位置包含的格子,最大偏移,待覆盖区域包含的格子
{
this->m = m;
for (auto& g2 : g) {
for (int i = 0; i < maxDr; i++)for (int j = 0; j < maxDc; j++)for(int k=0;k<maxDh;k++) {
for (auto& x : g2)x.r += i, x.c += j, x.h += k;
if (inBoard(g2))grids.push_back(g2);
for (auto& x : g2)x.r -= i, x.c -= j, x.h -= k;;
}
}
}
Block() {}
private:
map<Grid, int>m;
bool inBoard(vector<Grid>& g)
{
for (auto& x : g)if (!m[x])return false;
return true;
}
};
vector<vector<Grid>> Cover(vector<Block>blocks, map<int,int>ids, map<Grid, int>& mg)//所有块,不限数量的块的id, 待覆盖区域包含的格子编号为1,2,3...
{
int m = 0, maxNum = 0;
for (auto& block : blocks) {
m += block.grids.size();
maxNum += block.grids.size() * (block.grids[0].size() + 1);
}
DancingLink d(m, mg.size() + blocks.size() - ids.size(), maxNum);
int r = 0, c = mg.size();
map<int, int>mrow;
for (int i = 0; i < blocks.size(); i++) {
mrow[r + 1] = i + 1;
for (auto& grids : blocks[i].grids) {
++r;
for (auto& g : grids)d.push(r, mg[g]);
if(ids[i]==0)d.push(r, ++c);
}
}
d.dfs();
vector<int> rows = d.rows;
vector<vector<Grid>> ans;
for (auto row : rows) {
int id = 0;
while (!mrow[row])row--, id++;;
ans.push_back(blocks[mrow[row] - 1].grids[id]);
}
return ans;
}应用示例:
三维T型拼图
int r,c,h,blockNum; //自定义行列数,块数
map<Grid, int> ng,mg; //ng是自定义挖掉的格子,mg是有效格子
vector<Block>blocks;//自定义每个块的所有形态在最小位置包含的格子
map<int, int>ids;
vector<Grid> rotate(vector<Grid>& g)
{
int maxRow = 0, t;
for (auto& gi : g)maxRow = max(maxRow, gi.r);
for (auto& gi : g)t = gi.c, gi.c = maxRow - gi.r, gi.r = t;
return g;
}
vector<Grid> rotate2(vector<Grid> g)
{
int maxH = 0, t;
for (auto& gi : g)maxH = max(maxH, gi.h);
for (auto& gi : g)t = gi.c, gi.c = maxH - gi.h, gi.h = t;
return g;
}
void init1()
{
r = 6, c = 6, h=6, blockNum = 1;
ng.clear(), mg.clear();
}
void init2()
{
vector<Grid>v1 = { {0,0,0},{0,1,0},{0,2,0},{1,1,0} };
vector<Grid>v2 = { {0,0,0},{0,1,0},{0,2,0},{0,1,1} }, v3 = rotate2(v2), v4 = rotate2(v3), v5 = rotate2(v4);
blocks[0] = Block{ { v1,rotate(v1),rotate(v1),rotate(v1),v2,rotate(v2),v3,rotate(v3),v4,rotate(v4),v5,rotate(v5)}, r, c,h, mg };
ids[0] = 1;
}
void solve()
{
init1();
int id = 0;
for (int i = 0; i < r; i++)for (int j = 0; j < c; j++) for (int k = 0; k < h; k++) {
if (ng[Grid{ i, j ,k }] == 0)mg[Grid{ i, j,k }] = ++id;
}
blocks.resize(blockNum);
init2();
vector<vector<Grid>> grids = Cover(blocks,ids, mg);
vector<vector<vector<int>>>v(r);
for (int i = 0; i < r; i++) {
v[i].resize(c);
for (int j = 0; j < c; j++)v[i][j].resize(h);
}
for (int i = 0; i < grids.size(); i++) {
for (auto& g : grids[i])v[g.r][g.c][g.h] = i + 1;
}
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
for (int k = 0; k < h; k++)cout << v[i][j][k] << " ";
cout << endl;
}
cout << endl;
}
}
int main()
{
ios::sync_with_stdio(false);
clock_t start, endd;
start = clock();
freopen("D:ans.txt", "w", stdout);
solve();
endd = clock();
double endtime = (double)(endd - start) / CLOCKS_PER_SEC;
cout << "Total time:" << endtime << endl; //s为单位
return 0;
}输出:
1 1 1 2 2 2
7 7 7 10 10 10
20 20 20 23 23 23
21 21 21 31 31 31
24 21 37 36 31 32
3 3 3 4 4 4
5 1 8 9 2 11
13 7 9 9 10 27
25 20 35 9 23 27
28 35 35 35 49 27
24 37 37 36 32 32
24 3 39 36 4 33
5 5 8 8 11 11
13 13 34 42 42 42
25 25 34 34 42 27
28 28 34 49 49 49
24 30 37 36 48 32
26 39 39 41 33 33
5 14 8 43 44 11
13 29 43 43 43 54
25 29 29 50 54 54
28 29 50 50 50 54
30 30 40 48 48 48
26 26 39 41 41 33
14 14 14 44 44 44
16 16 16 51 51 51
18 16 17 52 51 53
18 18 40 52 52 47
18 30 40 52 47 47
26 19 40 41 38 47
6 6 6 12 12 12
15 6 17 45 12 53
15 15 17 45 45 53
15 22 17 45 46 53
22 22 22 46 46 46
19 19 19 38 38 38
Total time:0.953
匹配问题
给定一个2n个点的无向图,选出n条边,刚好覆盖这2n个点。
我用最新的代码,实现了求出所有解的代码:
//给定一个2n个点的图,选出n条边,刚好覆盖这2n个点
static vector<vector<Edge>> getEdgeCover(int n, vector<Edge>& v)
{
DancingLink d(v.size(), n * 2, v.size() * 2);
for (int i = 0; i < v.size(); i++) {
d.push(i, v[i].a + 1);
d.push(i, v[i].b + 1);
}
vector<vector<Edge>>ans;
vector<vector<int>> vrow = d.getAllAns();
for (auto vi : vrow)ans.push_back(fgetNumFromId(v, vi));
return ans;
}对称之美
对称之美自动求解
分组数字搜索算法
我们把标准数独和不规则数独放在一起,抽象成基于分组的数字搜索问题。
一些代码复用了本文前面的代码和搜索算法模板里面的代码。
class SearchWithGroupSum //分组数字搜索算法
{
public:
SearchWithGroupSum(vector<vector<int>>& gridGroup, int row, int col, int low, int high) :gridGroup{ gridGroup },row { row }, col{ col },low{low},high{high}
{
anti.resize(row*col);
grid.resize(row*col);
for (int g = 0; g < gridGroup.size(); g++) {
for (int i = 0; i < gridGroup[g].size(); i++)anti[gridGroup[g][i]].push_back(g);
maxNum += gridGroup[g].size();
}
}
void setGrid(vector<int>& grid)//除了已知数字之外都填0,有type=1的格子时需要调用本接口
{
this->grid = grid;
}
void setType(vector<int>& type)//有type=1或-1的格子时需要调用本接口
{
this->type = type;
}
vector<int> getAnyAns()
{
int m = 0;
for (auto k : type) {
if (k == 0)m += high - low + 1;
else if (k == 1)m += 1;
}
int n = gridGroup.size()*(high - low + 1) + row * col;
DancingLink d(m, n, (maxNum+row*col)*(high-low+1));
int r = 0;
map<int, int>mrow;
mrow[0] = -1;
for (int i = 0; i < row*col; i++) {
if (type[i] == -1)continue;
int lw = low, hh = high;
if (type[i] == 1)lw = hh = grid[i];
for (int x = lw; x <= hh; x++) {
d.push(++r, i + 1);
for (auto k : anti[i]) {
d.push(r, k*(high - low + 1) + x - low + row * col + 1);
}
mrow[r] = i;
}
}
vector<int> ans = d.getAnyAns();
for (auto rowId : ans) {
int id = mrow[rowId];
grid[id] += type[id]?0:low;
while (id == mrow[rowId - 1])rowId--, grid[id]++;
}
return grid;
}
private:
int row, col;//网格行列数
int low, high;//每个格子填入数字的范围是[low,high], 限制一:low>0
vector<int>type;//标识所有格子类型,0是需要填数字,1是已知数字,-1是无效格子
vector<int>grid;//所有格子中的数字
vector<vector<int>>gridGroup;//每一组有哪些格子
vector<vector<int>>anti;//每个格子属于哪些组
int maxNum = 1;
};标准数独
string Sudoku(string s, char cEmpty = '.')
{
vector<vector<int>>gridGroup;
vector<int>v;
for (int i = 0; i < 9; i++) {
v.clear();
for (int j = 0; j < 9; j++)v.push_back(i * 9 + j);
gridGroup.push_back(v);
v.clear();
for (int j = 0; j < 9; j++)v.push_back(j * 9 + i);
gridGroup.push_back(v);
}
for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++) {
v.clear();
for (int r = i * 3; r < i * 3 + 3; r++)for (int c = j * 3; c < j * 3 + 3; c++)v.push_back(r * 9 + c);
gridGroup.push_back(v);
}
SearchWithGroupSum opt(gridGroup, 9, 9, 1, 9);
vector<int>grid(81);
vector<int>type(81);
for (int i = 0; i < 81; i++)if (s[i] != cEmpty)grid[i] = s[i] - '0', type[i] = 1;
opt.setGrid(grid);
opt.setType(type);
v = opt.getAnyAns();
string ans(81, '0');
for (int i = 0; i < 81; i++)ans[i] = v[i] + '0';
return ans;
}
int main()
{
ios::sync_with_stdio(false);
string s;
while (cin >> s)
{
auto s1 = clock();
if (s == "end")return 0;
cout << Sudoku(s) << endl;
auto e1 = clock();
cout << endl << e1 - s1;
}
return 0;
}输入
.2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.
......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
输出
527389416819426735436751829375692184194538267268174593643217958951843672782965341
416837529982465371735129468571298643293746185864351297647913852359682714128574936
各耗时1毫秒
不规则数独
string Sudoku(string s, vector<int>&par, char cEmpty = '.', int parEmpty = -1)
{
vector<vector<int>>gridGroup;
vector<int>v;
map<int, vector<int>>m;
for (int i = 0; i < 9; i++) {
v.clear();
for (int j = 0; j < 9; j++)v.push_back(i * 9 + j);
gridGroup.push_back(v);
v.clear();
for (int j = 0; j < 9; j++) {
v.push_back(j * 9 + i);
if (par[i * 9 + j] != parEmpty)m[par[i * 9 + j]].push_back(i * 9 + j);
}
gridGroup.push_back(v);
}
for (auto mi : m)gridGroup.push_back(mi.second);
vector<int> groupSum(27, 45);
SearchWithGroupSum opt(gridGroup, 9, 9, 1, 9);
vector<int>grid(81);
vector<int>type(81);
for (int i = 0; i < 81; i++)if (s[i] != cEmpty)grid[i] = s[i] - '0', type[i] = 1;
opt.setGrid(grid);
opt.setType(type);
v = opt.getAnyAns();
string ans(81, '0');
for (int i = 0; i < 81; i++)ans[i] = v[i] + '0';
return ans;
}
int main()
{
ios::sync_with_stdio(false);
string s;
vector<int>par(81);
while (cin >> s)
{
for (int i = 0; i < 81; i++)cin >> par[i];
auto s1 = clock();
if (s == "end")return 0;
cout << Sudoku(s, par) << endl;
auto e1 = clock();
cout << endl << e1 - s1;
}
return 0;
}输入
.3.159.8.2.9...6.3..78.34..9...4...57.6...1.83...9...6..29.75..5.1...8.2.7.516.2.
1 2 2 3 3 3 4 4 4
1 2 2 3 3 3 4 4 4
1 2 2 2 3 3 4 4 4
1 2 5 2 5 3 6 6 6
1 1 5 5 5 5 5 6 6
1 1 1 8 5 9 5 9 6
7 7 7 8 8 9 9 9 6
7 7 7 8 8 8 9 9 6
7 7 7 8 8 8 9 9 6
输出
634159287259478613127863459918642375746325198385291746462987531591734862873516924
耗时0毫秒
分组定和数字搜索算法
和搜索算法模板不同的是,这里我们把数字互斥分组、数字定和分组2个概念分开处理。
所有分组都是数字互斥分组,但只有部分分组是数字定和分组。
我们把使用场景限定为,数字定和分组之间没有重复的格子,但是可以有格子不在任一数字定和分组之内。
set<int> ToSet(int low, int high)
{
set<int>ans;
for (int i = low; i <= high; i++)ans.insert(i);
return ans;
}
class SearchWithGroupSum //分组搜索算法
{
public:
SearchWithGroupSum(vector<vector<int>>& gridGroup, vector<vector<int>>& gridGroup2,const map<int, vector<vector<int>>> &spRet, int row, int col, int low, int high)
:gridGroup{ gridGroup }, gridGroup2{ gridGroup2 },spRet{ spRet }, row{ row }, col{ col }, low{ low }, high{ high }
{
anti.resize(row*col);
grid.resize(row*col);
for (int g = 0; g < gridGroup.size(); g++) {
for (int i = 0; i < gridGroup[g].size(); i++)anti[gridGroup[g][i]].push_back(g);
}
}
void setGrid(vector<int>& grid)//除了已知数字之外都填0,有type=1的格子时需要调用本接口
{
this->grid = grid;
}
void setType(vector<int>& type)//有type=1或-1的格子时需要调用本接口
{
this->type = type;
}
vector<int> getAnyAns()
{
int m = (high - low + 1) * row * col + NumInVec2D(GetSecond(spRet));
int n = gridGroup.size() * (high - low + 1) + row * col;
DancingLink d(m, n, (row * col + NumInVec2D(GetSecond(spRet)))*(high - low + 1) * row);
int r = 0;
map<int, int>mrow, mrow2;
mrow[0] = -1;
map<int, int>visit;
for (auto &mp : spRet) {
auto &sp = mp.second;
for (int i = 0; i < sp.size();i++) {
auto &v = sp[i];
mrow[++r] = i, mrow2[r] = mp.first;
for (int i = 0; i < v.size(); i++) {
d.push(r, gridGroup2[mp.first][i] + 1);
for (auto k : anti[gridGroup2[mp.first][i]]) {
d.push(r, k*(high - low + 1) + v[i] - low + row * col + 1);
}
visit[gridGroup2[mp.first][i]] = 1;
}
}
}
int kr = r;
for (int i = 0; i < row*col; i++) {
if (type[i] == -1 || visit[i] == 1)continue;
int lw = low, hh = high;
if (type[i] == 1)lw = hh = grid[i];
for (int x = lw; x <= hh; x++) {
mrow[++r] = i;
d.push(r, i + 1);
for (auto k : anti[i]) {
d.push(r, k*(high - low + 1) + x - low + row * col + 1);
}
}
}
vector<int> ans = d.getAnyAns();
for (auto rowId : ans) {
if (rowId > kr) {
int id = mrow[rowId];
grid[id] += type[id] ? 0 : low;
while (rowId > kr + 1 && id == mrow[rowId - 1])rowId--, grid[id]++;
}
else {
int id = mrow[rowId];
auto v = spRet[mrow2[rowId]][id];
for (int i = 0; i < gridGroup2[mrow2[rowId]].size(); i++)grid[gridGroup2[mrow2[rowId]][i]] = v[i];
}
}
return grid;
}
private:
int row, col;//网格行列数
int low, high;//每个格子填入数字的范围是[low,high], 限制一:low>0
vector<int>type;//标识所有格子类型,0是需要填数字,1是已知数字,-1是无效格子
vector<int>grid;//所有格子中的数字
vector<vector<int>>gridGroup;//互斥组,每一组有哪些格子
vector<vector<int>>gridGroup2;//定和组,每一组有哪些格子
vector<vector<int>>anti;//每个格子属于哪些组
map<int, vector<vector<int>>> spRet;
};
满覆盖杀手数独
map<int, vector<vector<int>>> getSplitRet(vector<vector<int>>& gridGroup, map<int, int>&groupSum)
{
return MapTrans<int, int, vector<vector<int>>>(groupSum, [&](pair<int, int>p) {
return IntSplitA(groupSum[p.first], gridGroup[p.first].size(), ToSet(1, 9));
});
}
string Sudoku(string s, vector<int>&par, vector<int>&groupSum, char cEmpty = '.', int parEmpty = -1)
{
vector<vector<int>>gridGroup, gridGroup2;
vector<int>v;
map<int, vector<int>>m;
for (int i = 0; i < 9; i++) {
v.clear();
for (int j = 0; j < 9; j++)v.push_back(i * 9 + j);
gridGroup.push_back(v);
v.clear();
for (int j = 0; j < 9; j++) {
v.push_back(j * 9 + i);
if (par[i * 9 + j] != parEmpty)m[par[i * 9 + j]].push_back(i * 9 + j);
}
gridGroup.push_back(v);
}
for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++) {
v.clear();
for (int r = i * 3; r < i * 3 + 3; r++)for (int c = j * 3; c < j * 3 + 3; c++)v.push_back(r * 9 + c);
gridGroup.push_back(v);
}
for (auto mi : m)gridGroup2.push_back(mi.second);
map<int, int>mGroupSum;
for (int i = 0; i < groupSum.size(); i++)mGroupSum[i] = groupSum[i];
auto spRet = getSplitRet(gridGroup2, mGroupSum);
SearchWithGroupSum opt(gridGroup, gridGroup2, spRet, 9, 9, 1, 9);
vector<int>grid(81);
vector<int>type(81);
for (int i = 0; i < 81; i++)if (s[i] != cEmpty)grid[i] = s[i] - '0', type[i] = 1;
opt.setGrid(grid);
opt.setType(type);
v = opt.getAnyAns();
string ans(81, '0');
for (int i = 0; i < 81; i++)ans[i] = v[i] + '0';
return ans;
}
int main()
{
ios::sync_with_stdio(false);
string s;
vector<int>groupSum;
vector<int>par(81);
while (cin >> s)
{
int x;
while (cin >> x) {
if (x == 0)break;
groupSum.push_back(x);
}
for (int i = 0; i < 81; i++)cin >> par[i];
auto s1 = clock();
if (s == "end")return 0;
cout << Sudoku(s, par, groupSum) << endl;
auto e1 = clock();
cout << endl << e1 - s1;
}
return 0;
}输入:
.................................................................................
15 24 11 17 5 14 10 16 10 15 10 9 10 21 7 20 15 15 12 17 8 16 18 10 13 12 13 32 10 0
1 2 3 3 5 5 8 8 8
1 2 2 4 6 7 7 9 9
1 2 2 4 6 6 14 15 9
10 10 12 13 13 14 14 15 16
11 11 12 19 18 17 17 16 16
20 19 19 19 18 22 17 16 23
20 20 21 21 22 22 22 23 23
24 25 25 25 25 28 28 28 28
24 26 26 27 27 27 29 29 28
输出:
946532781183974652527816943691287534378495216452163897765348129814629375239751468
耗时40毫秒
非满覆盖杀手数独
代码和满覆盖杀手数独完全相同。
输入:
.................................................................................
26 14 16 12 16 6 14 14 12 8 20 12 26 22 6 6 38 16 14 6 14 0
-1 1 2 2 3 3 -1 4 -1
1 1 1 5 5 3 -1 4 4
6 1 -1 5 5 8 8 -1 7
6 9 9 -1 10 10 11 12 7
13 13 13 14 -1 10 11 12 12
15 13 13 14 14 -1 11 11 21
15 -1 16 16 17 17 -1 -1 21
18 -1 -1 17 17 17 -1 19 19
18 18 -1 17 17 20 20 19 -1
输出:
956834217742169583183725946539241768867953124214678395421587639395416872678392451
耗时274毫秒