目录
- 概要
- 前向过程
- nice property
- 逆向过程
- 参数推导
- 简化
- 参考资料
概要
Denoising Diffusion Probabilistic Model(DDPM)是一个生成模型,给定一个目标分布,学习模型以便可以从目标分布中采样。
使用马尔科夫链建模。输入是噪声,通过神经网络逐步去噪,最终产生的输出符合目标分布。
生成的数据可以是任意的,可以是图像也可以语音。目前diffusion model主要用于图像生成,所以后面将以图像生成为例介绍。
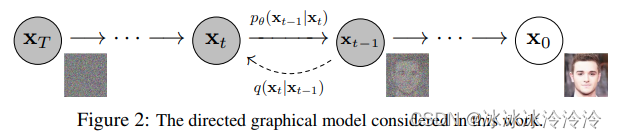
diffusion model分为两个过程:
- 预定义的前向过程(forward diffusion process):一步步往图像中加入噪声,直到图像变成纯噪声。该过程的形式和参数都是人为定义的。
- 需要学习的逆向过程(reverse denoising diffusion process):一步步从纯噪声中去噪,直到得到图像。该过程用一个可学习的神经网络表示。
前向过程和逆向过程都分为 T T T步。图像的生成使用逆向过程。
diffusion model是隐变量模型 p θ ( x 0 ) : = ∫ p θ ( x 0 : T ) d x 1 : T p_\theta(\mathbf{x}_0):=\int p_\theta(\mathbf{x}_{0:T})d\mathbf{x}_{1:T} pθ(x0):=∫pθ(x0:T)dx1:T,其中 x 0 ∼ q ( x 0 ) \mathbf{x}_0\sim q(\mathbf{x}_0) x0∼q(x0)是可观测变量, x 1 , x 2 , . . . , x T \mathbf{x}_1,\mathbf{x}_2,...,\mathbf{x}_T x1,x2,...,xT是隐标量并且和可观测变量 x 0 \mathbf{x}_0 x0有相同的维度。
前向过程
真实数据的分布为
q
(
x
0
)
q(\mathbf{x}_0)
q(x0),前向过程是一个预定义的马尔科夫链,其中
q
(
x
t
∣
x
t
−
1
)
q(\mathbf{x}_t | \mathbf{x}_{t-1})
q(xt∣xt−1)加入高斯噪声:
q
(
x
t
∣
x
t
−
1
)
=
N
(
x
t
;
1
−
β
t
x
t
−
1
,
β
t
I
)
q(\mathbf{x}_t | \mathbf{x}_{t-1})=\mathcal{N}(\mathbf{x}_t;\sqrt{1−\beta_t}\mathbf{x}_{t−1},\beta_t\mathbf{I})
q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)其中
0
<
β
1
<
β
2
<
.
.
.
<
β
T
<
1
0<\beta_1<\beta_2<...<\beta_T<1
0<β1<β2<...<βT<1是预定义的数值,可以用不同的variance schedule定义。
从
q
(
x
0
)
q(\mathbf{x}_0)
q(x0)开始,逐步加入高斯噪声,生成
x
1
,
x
2
,
.
.
.
,
x
T
\mathbf{x}_1,\mathbf{x}_2,...,\mathbf{x}_T
x1,x2,...,xT。如果variance schedule的选择合适,
x
T
\mathbf{x}_T
xT将是纯高斯噪声。
nice property
根据我们定义的前向过程,一个好的性质是
x
t
\mathbf{x}_t
xt可以直接采样从
x
0
\mathbf{x}_0
x0采样得到(高斯的和已经是高斯),而不需要一步一步地采样:
q
(
x
t
∣
x
0
)
=
N
(
x
t
;
α
ˉ
t
x
0
,
(
1
−
α
ˉ
t
)
I
)
q(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\sqrt{\bar{\alpha}_t}\mathbf{x}_0,(1-\bar{\alpha}_t){\mathbf{I}})
q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)其中
α
t
:
=
1
−
β
t
,
α
ˉ
t
:
=
Π
s
=
1
t
α
s
\alpha_t :=1−\beta_t, \bar{\alpha}_t := \Pi_{s=1}^{t} \alpha_s
αt:=1−βt,αˉt:=Πs=1tαs。
因为
β
t
\beta_t
βt是variance schedule定义的,所以
α
t
\alpha_t
αt也都是已知的。
逆向过程
逆向过程被定义为一个从
p
(
x
T
)
=
N
(
x
T
;
0
,
I
)
p(\mathbf{x}_T)=\mathcal{N}(\mathbf{x}_T;\mathbf{0},\mathbf{I})
p(xT)=N(xT;0,I)出发的马尔科夫链。
前向过程的形式和参数都是预定义的,但后向过程
p
(
x
t
−
1
∣
x
t
)
p(\mathbf{x}_{t-1} | \mathbf{x}_t)
p(xt−1∣xt)的形式和参数未知的,因为要计算这个条件概率需要知道所有可观测变量的分布。
我们使用一个神经网络来近似这个条件概率,近似概率用
p
θ
(
x
t
−
1
∣
x
t
)
p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t)
pθ(xt−1∣xt)表示,其中
θ
\theta
θ是神经网络的参数,使用梯度下降法优化。
我们并不知道
p
(
x
t
−
1
∣
x
t
)
p(\mathbf{x}_{t-1} | \mathbf{x}_t)
p(xt−1∣xt)的形式和参数,这里我们假设它是高斯的。高斯分布有两个参数,分别是均值
μ
θ
\mu_\theta
μθ和方差
Σ
θ
\Sigma_\theta
Σθ,所以逆向过程可以表示为:
p
θ
(
x
t
−
1
∣
x
t
)
=
N
(
x
t
−
1
;
μ
θ
(
x
t
,
t
)
,
Σ
θ
(
x
t
,
t
)
)
p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_{t})=\mathcal{N}(\mathbf{x}_{t-1} ; \mu_\theta(\mathbf{x}_{t},t),\Sigma_\theta(\mathbf{x}_{t},t))
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))使用神经网络学习均值和方差。特别地,DDPM的作者将方差固定为常数,只学习均值。
参数推导
参数推导推导的是逆向过程中的参数。
diffusion model是隐变量模型
p
θ
(
x
0
)
:
=
∫
p
θ
(
x
0
:
T
)
d
x
1
:
T
p_\theta(\mathbf{x}_0):=\int p_\theta(\mathbf{x}_{0:T})d\mathbf{x}_{1:T}
pθ(x0):=∫pθ(x0:T)dx1:T。
考虑最大化log likelihood来学习参数,但因为隐变量模型的likelihood没法直接表示,一般都是采用优化log likelihood的下界variational lower bound (ELBO)。
在diffusion model中,为了方便神经网络优化,我们将最大化问题转换为最小化问题,优化的目标是:
E
[
−
log
p
θ
(
x
0
)
]
≤
E
q
[
−
log
p
θ
(
x
0
:
T
)
q
(
x
1
:
T
∣
x
0
)
]
=
E
q
[
−
log
p
(
x
T
)
−
∑
t
≥
1
log
p
θ
(
x
t
−
1
∣
x
t
)
q
(
x
t
∣
x
t
−
1
)
]
:
=
L
\mathbb{E}[-\log p_\theta(\mathbf{x}_0)]\leq \mathbb{E}_q[-\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}]= \mathbb{E}_q[-\log p_(\mathbf{x}_T)-\sum_{t\geq1}\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})}]:=L
E[−logpθ(x0)]≤Eq[−logq(x1:T∣x0)pθ(x0:T)]=Eq[−logp(xT)−t≥1∑logq(xt∣xt−1)pθ(xt−1∣xt)]:=L
L
L
L可以重写为
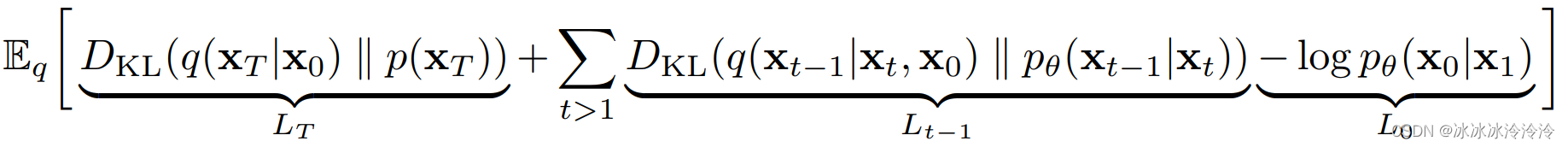
其中
q
(
x
t
−
1
∣
x
t
,
x
0
)
q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)
q(xt−1∣xt,x0)是高斯分布:
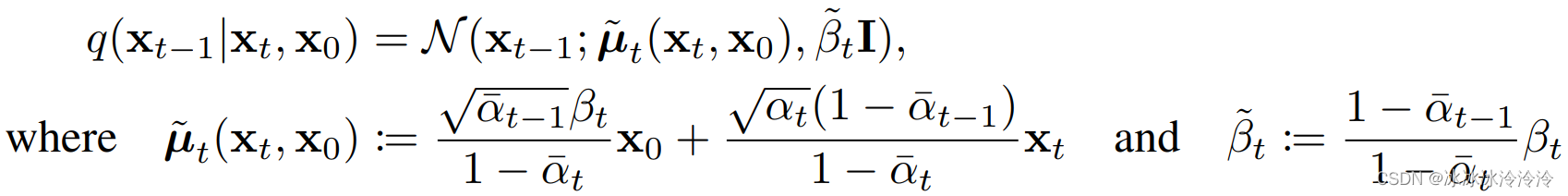
因为
L
L
L中都是高斯函数的KL散度,有闭合(closed form)的表达式。优化时将分别考虑各个
L
t
L_t
Lt。
- 其中因为 β t \beta_t βt是预定义的, L T L_T LT是一个常数可以忽略。
- L 0 L_0 L0是使用一个单独的离散解码器。
-
L
t
−
1
L_{t-1}
Lt−1可以写为:
L t − 1 = E x 0 , ϵ [ 1 2 σ 2 ∥ μ ~ t ( x t , x 0 ) − μ θ ( x t , t ) ∥ 2 ] + C L_{t-1}=\mathbb{E}_{\mathbf{x}_0,\epsilon}[\frac{1}{2\sigma^2}\|\tilde\mu_t(\mathbf{x}_t,\mathbf{x}_0)-\mu_\theta(\mathbf{x}_t,t)\|^2]+C Lt−1=Ex0,ϵ[2σ21∥μ~t(xt,x0)−μθ(xt,t)∥2]+C L t − 1 L_{t-1} Lt−1经过带入公式以及参数化的技巧,优化目标变为
E x 0 , ϵ [ β t 2 2 σ t 2 α t ( 1 − α ˉ t ) ∥ ϵ − ϵ θ ( α ˉ t x 0 + ( 1 − α ˉ t ) ϵ , t ) ∥ 2 ] \mathbb{E}_{\mathbf{x}_0,\epsilon}[\frac{\beta^2_t}{2\sigma_t^2\alpha_t(1-\bar\alpha_t)}\|\epsilon-\epsilon_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{(1-\bar{\alpha}_t)}\epsilon,t)\|^2] Ex0,ϵ[2σt2αt(1−αˉt)βt2∥ϵ−ϵθ(αˉtx0+(1−αˉt)ϵ,t)∥2]网络学习的是添加的噪声, μ θ ( x t , t ) \mu_\theta(\mathbf{x}_{t},t) μθ(xt,t)可以由下面的公式计算得到 μ θ ( x t , t ) = 1 α t ( x t − β t 1 − α ˉ t ϵ θ ( x t , t ) ) \mu_\theta(\mathbf{x}_{t},t)=\frac{1}{\sqrt{\alpha_t}}(\mathbf{x}_{t}-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\epsilon_\theta(\mathbf{x_t,t})) μθ(xt,t)=αt1(xt−1−αˉtβtϵθ(xt,t))
简化
L
t
−
1
L_{t-1}
Lt−1可以进行简化,简化后的目标是:
E
x
0
,
ϵ
∥
ϵ
−
ϵ
θ
(
α
ˉ
t
x
0
,
(
1
−
α
ˉ
t
)
ϵ
,
t
)
∥
2
\mathbb{E}_{\mathbf{x}_0,\epsilon}\|\epsilon-\epsilon_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0,\sqrt{(1-\bar{\alpha}_t)}\epsilon,t)\|^2
Ex0,ϵ∥ϵ−ϵθ(αˉtx0,(1−αˉt)ϵ,t)∥2简化版删去了原有的权重,所以是一个加权的变分界,其减小了
t
t
t较小时的权重。实验显示简化版的优化目标效果更好。
参考资料
NIPS 2020《Denoising Diffusion Probabilistic Models》
Hugging Face blog《The Annotated Diffusion Model》
Lil’Log《What are Diffusion Models?》



![[附源码]Node.js计算机毕业设计儿童成长记录与分享系统Express](https://img-blog.csdnimg.cn/922237a72f9e44fb904dc81c8ef0354a.png)


![[附源码]Node.js计算机毕业设计电影推荐网站Express](https://img-blog.csdnimg.cn/726af46614cd4a719680eb4a6aa5a235.png)


![P3884 [JLOI2009]二叉树问题——树化图Floyd+dfs](https://img-blog.csdnimg.cn/img_convert/88dd83b356031d1d877bafebad61c922.png)
![[附源码]Python计算机毕业设计Django高校体育场馆管理系统](https://img-blog.csdnimg.cn/a1e2e49d3625467e99151179bc8873b0.png)