寻找峰值 peak

给出一个数组 a b c d e f g h i
并给予数字 index 1 2 3 4 5 6 7 8 9
那么如果某个数字是 peak ，那么他将 大于等于左边的数 且 大于等于右边的数
或者 a >= b 这里的 a 也是峰值

暴力算法

简单的暴力算法思路即：从左往右遍历
复杂度显然为：O(n)
那么看看能否改进一下暴力算法？

分而治之

Use a divide and conquer strategy, and recursively break;
判断 a[n/2] 和 a[n/2-1] 和 a[n/2] 和 a[n/2+1] 进行二分答案搜索
这就使得复杂度降为：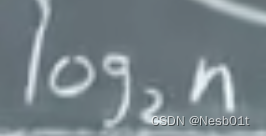
在同样情况下，运行暴力算法需要13秒，使用分而治之策略只花0.001秒
详细的算法实现可以参考：CSDN 作者链接

从1D到2D

一维的问题解决了，那么思考如果问题来到二维呢？
此时的 peek 会定义为 a>=b, a>=c, a>=d, a>=e

朴素算法

课中的教师称之为 Greedy Ascent 算法，从一个地方出发，逐渐往最高的数字移动：

Attemp#2

• 寻找一个 Middle Column，即 j = m / 2
• Find global maximum on Column j at (i, j)
• 比较 (i, j-1) (i, j) (i, j+1)
• 如果 (i, j-1) > (i, j) 选择左边的一列！
• 最终，如果 (i, j) >= (i ,j-1), (i, j+2)，那么 (i, j) 就是一个 2D peak