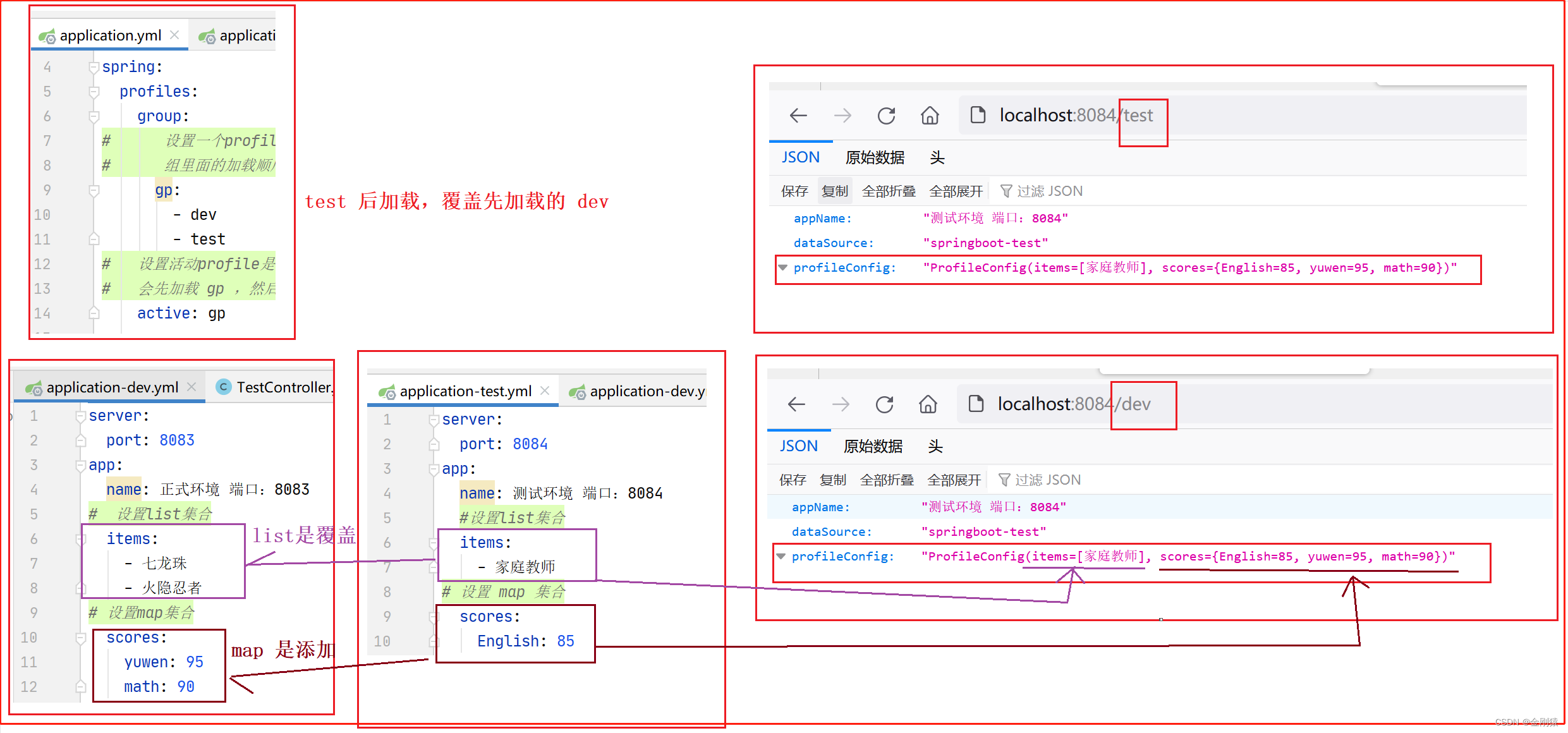
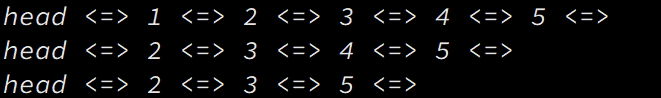思路

作为一种高效的排序算法，它主要是通过递归来实现的，具体步骤如下

• 划分问题：将序列划分成数量尽量相等的两部分
• 递归求解：将两部分分别排序
• 合并问题：将两个序列合并成一个

前两步对于笔者来说肯定是很容易实现的，归并排序的难点主要在第三步
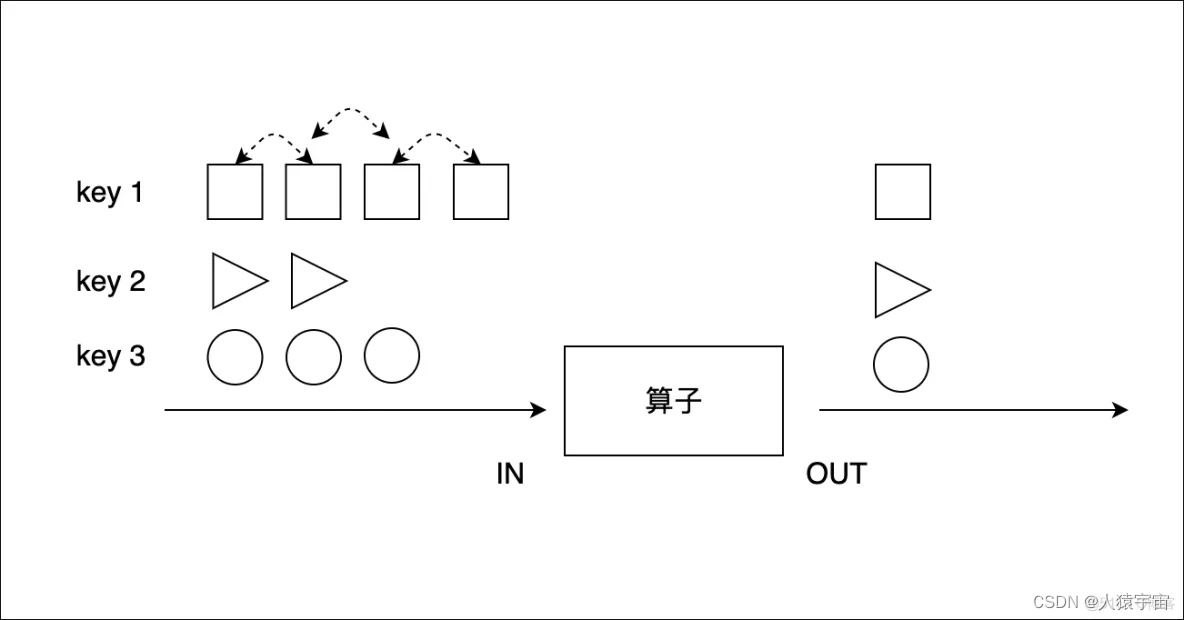
如何合并两个有序序列呢？很明显，只需要每次选择两个序列中的最小元素并将其添加到辅助空间（最终答案）中，如图所示

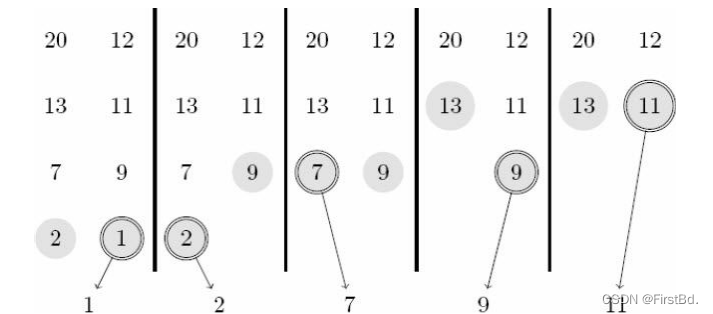
代码

void merge_sort(int *A,int l,int r,int *T){//对[l,r)区间排序
	if(r-l<=1) return;
	int mid=l+(r-l)/2;
	merge_sort(A,l,mid,T),merge_sort(A,mid,r,T);
	int i=l,p=l,q=mid;
	while(p<mid||q<r)
		if(q>=r||(p<mid&&A[p]<=A[q])) T[i++]=A[p++];
		else T[i++]=A[q++];
	for(i=l;i<r;i++) A[i]=T[i];
}

这段代码最难理解的部分是while循环部分：
在通过递归将两边序列排序后，我们就是按照图解的方式来合并
$while(p<mid||q<r)$的意思为：只要有一个非空序列就继续合并
KaTeX parse error: Expected 'EOF', got '&' at position 16: if(q>=r||(p<mid&̲&A[p]<=A[q]))的意思为：如果右侧序列为空或者左侧序列非空且左侧序列的最小元素比右侧序列的最小元素小的情况下，将左序列的最小元素加入辅助空间
若是其他情况就将右序列的最小元素加入辅助空间

最后将辅助空间中所有元素放进原来的数组

相关问题——逆序对

思路

$n^2$的枚举是肯定会TLE的
非常幸运啊，这个逆序对是可以用归并排序顺便计算的

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=5e5+5;
int cnt,n;
int a[maxn],t[maxn];
void merge_sort(int *A,int l,int r,int *T){
	if(r-l<=1) return;
	int m=l+(r-l)/2;
	merge_sort(A,l,m,T),merge_sort(A,m,r,T);
	int i=l,q=l,p=m;
	while(p<m||q<r) if(q>=r||(p<m&&A[p]<=A[q])) T[i++]=A[p++]; else T[i++]=A[q++],cnt+=m-p;
	for(i=l;i<r;i++) A[i]=T[i];
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	merge_sort(a,1,n+1,t);
	cout<<cnt;
	return 0;
}

细心的读者已经发现了这个代码和归并排序的代码的不同之处：在else后面又跟了一个$cnt+=m-p$
当右边的$A_j$复制到T中时，左边还没来得及复制到T的那些数旧是左边所有比$A_j$大的数，所以在累加器中 加上左边元素个数$m-p$即可（左边所剩的元素在区间[p,m)中，因此元素个数为m-p）

end

完结撒花