【Megatron-DeepSpeed】张量并行工具代码mpu详解(三)：张量并行层的实现及测试

相关博客
【Megatron-DeepSpeed】张量并行工具代码mpu详解(三)：张量并行层的实现及测试
【Megatron-DeepSpeed】张量并行工具代码mpu详解(一)：并行环境初始化
【Megatron-DeepSpeed】张量并行工具代码mpu详解(二)：Collective通信操作的封装mappings
【深度学习】【分布式训练】DeepSpeed：AllReduce与ZeRO-DP
【深度学习】混合精度训练与显存分析
【深度学习】【分布式训练】Collective通信操作及Pytorch示例
【自然语言处理】【大模型】大语言模型BLOOM推理工具测试
【自然语言处理】【大模型】GLM-130B：一个开源双语预训练语言模型
【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍
【自然语言处理】【大模型】BLOOM：一个176B参数且可开放获取的多语言模型

Megatron-DeepSpeed：张量并行的实现及测试

Megatron-DeepSpeed是DeepSpeed版本的NVIDIA Megatron-LM。像BLOOM、GLM-130B等主流大模型都是基于Megatron-DeepSpeed开发的。这里以BLOOM版本的Megetron-DeepSpeed为例，介绍其模型并行代码mpu的细节(位于megatron/mpu下)。

理解该部分的代码需要对模型并行的原理以及集合通信有一定的理解，可以看文章：

【深度学习】【分布式训练】Collective通信操作及Pytorch示例
【深度学习】【分布式训练】一文捋顺千亿模型训练技术：流水线并行、张量并行和3D并行
【深度学习】【分布式训练】DeepSpeed：AllReduce与ZeRO-DP

强烈建议阅读，不然会影响本文的理解：

【Megatron-DeepSpeed】张量并行工具代码mpu详解(一)：并行环境初始化
【Megatron-DeepSpeed】张量并行工具代码mpu详解(二)：Collective通信操作的封装mappings

阅读建议：

本文仅会解析核心代码，并会不介绍所有代码；
本文会提供一些测试脚本来展现各部分代码的功能；
建议实际动手实操来加深理解；
建议对Collective通信以及分布式模型训练有一定理解，再阅读本文；

一、总览

mpu目录下核心文件有：

initialize.py：负责数据并行组、张量并行组和流水线并行组的初始化，以及获取与各类并行组相关的信息；
data.py：实现张量并行中的数据广播功能；
cross_entropy.py：张量并行版本的交叉熵；
layers.py：并行版本的Embedding层，以及列并行线性层和行并行线性层；
mappings.py：用于张量并行的通信操作；

二、1D张量并行原理

Megatron-DeepSpeed中的并行是1D张量并行，这里做简单的原理介绍。希望更深入全面的理解并行技术，可以阅读上面“千亿模型训练技术”的文章。
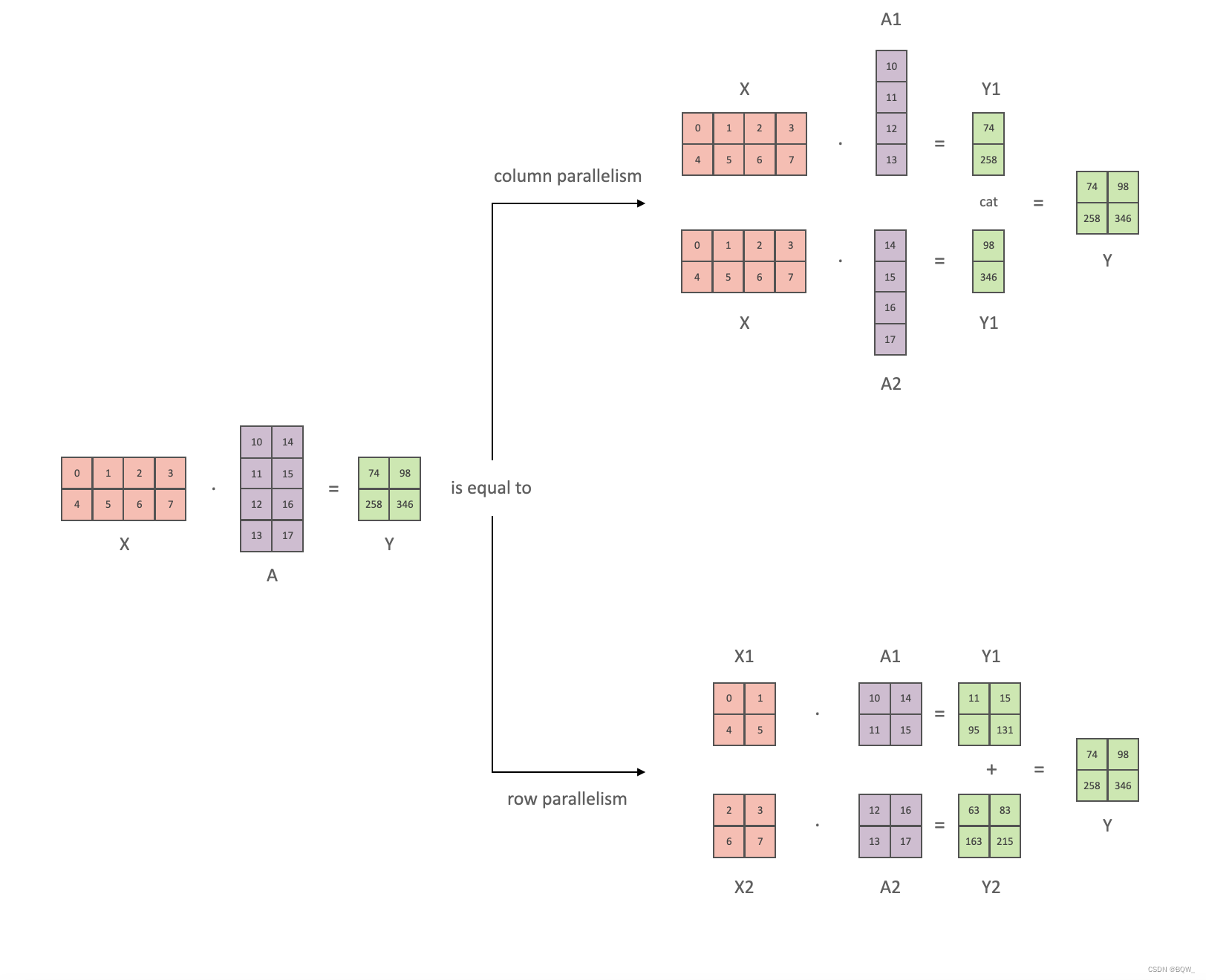
请添加图片描述

以全链接层 $Y = X A$ 为例，介绍1D张量并行。其中， $X$ 和 $Y$ 是输入和输出向量， $A$ 是权重矩阵。总量来说1D张量并行可以分为列并行和行并行(以权重矩阵的分割方式命名)，上图展示了两种并行。

列并行

将矩阵行列划分为n份(不一定必须相等大小)可以表示为 $A=[A_1,A_2, \dots, A_n]$ ，那么矩阵乘法表示为
$XA=X[A_1,A_2,\dots,A_n]=[XA_1,XA_2,\dots,XA_n]$
显然，仅需要对权重进行划分。
行并行

对权重进行划分，那么必须对输入矩阵也进行划分。假设要将 $A$ 水平划分为 $n$ 份，则输入矩阵 $X$ 必须垂直划分为 $n$ 份，矩阵乘法表示为
$XA=[X_1,X_2,\dots,X_n] \left[ \begin{array}{l} A_1 \\ A_2 \\ \dots \\ A_n \end{array} \right] = X_1A_1+X_2A_2+\dots+X_nA_n$

三、张量并行的实现及测试

1. 列并行

列并行在前向传播时，张量并行组中的进程独立前向传播即可。假设张量并行度为2，则神经网络的前向传播可以简单表示为：
$\begin{aligned} \text{loss}&=f(Y) = f([Y_1,Y_2]) \\ &=f([XA_1,XA_2]) \\ \end{aligned}$
反向传播时， $\text{loss}$ 对输入 $X$ 的梯度为
$KaTeX parse error: Undefined control sequence: \part at position 8: \frac{\̲p̲a̲r̲t̲ ̲f}{\part X}=\fr…$
因此，反向传播时需要对张量并行组中各个独立的梯度进行求和。

源代码

class ColumnParallelLinear(torch.nn.Module):
    """
    列并行线性层.
    线性层定义为Y=XA+b. A沿着第二维进行并行，A = [A_1, ..., A_p]
    
    参数:
    	input_size: 矩阵A的第一维度.
    	output_size: 矩阵A的第二维度.
    	bias: 若为true则添加bias.
    	gather_output: 若为true，在输出上调用all-gather，使得Y对所有GPT都可访问.
    	init_method: 随机初始化方法.
    	stride: strided线性层.
    """

    def __init__(self, input_size, output_size, bias=True, gather_output=True,
                 init_method=init.xavier_normal_, stride=1,
                 keep_master_weight_for_test=False,
                 skip_bias_add=False):
        super(ColumnParallelLinear, self).__init__()
        self.input_size = input_size
        self.output_size = output_size
        self.gather_output = gather_output
        # 获得张量并行组的world_size
        world_size = get_tensor_model_parallel_world_size()
        # 按照张量并行度(world_size)划分输出维度
        self.output_size_per_partition = divide(output_size, world_size)
        self.skip_bias_add = skip_bias_add

        # Parameters.
        # Note: torch.nn.functional.linear 执行 XA^T+b
        args = get_args()
        if args.use_cpu_initialization:
            # 初始化张量. 若完整权重矩阵A为n*m，张量并行度为k，这里初始化的张量为n*(m/k)
            # 也就是张量并行组中的进程各自初始化持有的部分张量
            self.weight = Parameter(torch.empty(self.output_size_per_partition,
                                                self.input_size,
                                                dtype=args.params_dtype))
            # 使用init_method对权重矩阵self.weight进行随机初始化(CPU版)
            # self.master_weight在测试中使用，这里不需要关注
            self.master_weight = _initialize_affine_weight_cpu(
                self.weight, self.output_size, self.input_size,
                self.output_size_per_partition, 0, init_method,
                stride=stride, return_master_weight=keep_master_weight_for_test)
        else:
            self.weight = Parameter(torch.empty(
                self.output_size_per_partition, self.input_size,
                device=torch.cuda.current_device(), dtype=args.params_dtype))
            # 使用init_method对权重矩阵self.weight进行随机初始化(GPU版)
            _initialize_affine_weight_gpu(self.weight, init_method,
                                          partition_dim=0, stride=stride)
            
        if bias:
            # 实例化一个bias
            if args.use_cpu_initialization:
                self.bias = Parameter(torch.empty(
                    self.output_size_per_partition, dtype=args.params_dtype))
            else:
                self.bias = Parameter(torch.empty(
                    self.output_size_per_partition,
                    device=torch.cuda.current_device(),
                    dtype=args.params_dtype))
            # 将张量并行的相关信息追加至self.bias
            set_tensor_model_parallel_attributes(self.bias, True, 0, stride)
            # bias初始化为0
            with torch.no_grad():
                self.bias.zero_()
        else:
            self.register_parameter('bias', None)

    def forward(self, input_):
        # 前向传播时input_parallel就等于input_
        # 反向传播时在张量并在组内将梯度allreduce
        input_parallel = copy_to_tensor_model_parallel_region(input_)
        bias = self.bias if not self.skip_bias_add else None
        output_parallel = F.linear(input_parallel, self.weight, bias)
        if self.gather_output:
            # 收集张量并行组内的张量并进行拼接
            # 此时，output是非张量并行情况下前向传播的输出
            # 张量并行组中的进程都持有完全相同的output
            output = gather_from_tensor_model_parallel_region(output_parallel)
        else:
            # 此时，output是张量并行情况下的前向传播输出
            # 张量并行组中的进程持有不同的output
            output = output_parallel
        output_bias = self.bias if self.skip_bias_add else None
        return output, output_bias

测试代码

测试遵循文章【Megatron-DeepSpeed】张量并行工具代码mpu详解(一)：并行环境初始化中的设置，张量并行度为2，且流水线并行度为2。

def test_column_parallel_linear():
    global_rank = torch.distributed.get_rank()
    tensor_model_parallel_size = mpu.get_tensor_model_parallel_world_size()
    # 设置随机数种子
    seed = 12345
    set_random_seed(seed)
    # 张量并行组中，各个进程持有张量的input_size
    input_size_coeff = 4 #
    # 张量并行组中，各个进程持有张量的output_size
    input_size = input_size_coeff * tensor_model_parallel_size
    output_size_coeff = 2
    output_size = output_size_coeff * tensor_model_parallel_size
    # 初始化一个产生二维张量的模拟网络，输入的张量为(batch_size, input_size)
    batch_size = 6
    identity_layer = IdentityLayer2D(batch_size, input_size).cuda()
    # 初始化一个列并行线性层
    linear_layer = mpu.ColumnParallelLinear(
        input_size, output_size, keep_master_weight_for_test=True, gather_output=False).cuda()
    # 随机初始化一个loss权重
    # 主要是为了计算标量的loss，从而验证梯度是否正确
    loss_weight = torch.randn([batch_size, output_size]).cuda()
    ## 前向传播
    input_ = identity_layer()
    # 此时，张量并行组中各个进程持有的output仅是完整输出张量的一部分
    output = linear_layer(input_)[0]

    if torch.distributed.get_rank() == 0:
        print(f"> Output size without tensor parallel is ({batch_size},{output_size})")
    torch.distributed.barrier()
    info = f"*"*20 + \
            f"\n> global_rank={global_rank}\n" + \
            f"> output size={output.size()}\n"
    print(info, end="")

测试结果

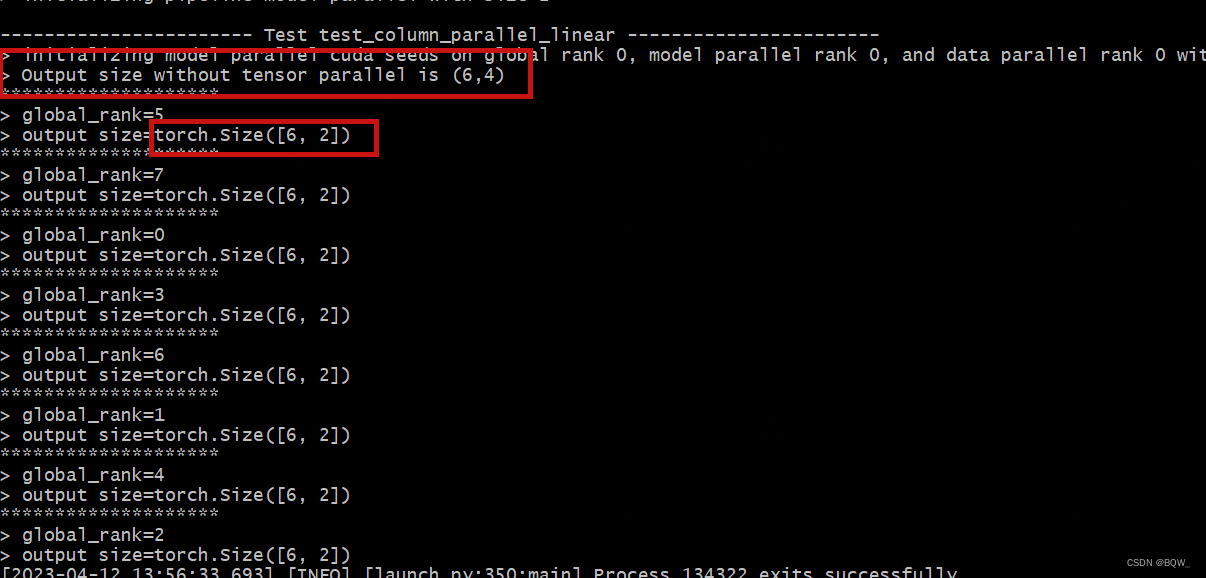
在这里插入图片描述

可以看到，没有并行情况下的期望输出为(6,4)。张量并行度为2的情况下，各个rank的输出维度为(6,2)。

2. 行并行

行并行在前向传播时，张量并行组中各个进程不仅要持有部分权重，也还持有部分的输入张量。前向传播的过程可以简单表示为
$\begin{aligned} \text{loss}&=f(Y) =f(XA)\\ &= f([X_1,X_2]\left[ \begin{array}{l} A_1 \\ A_2 \\ \end{array} \right]) \\ &=f([X_1A_1+X_2A_2]) \\ \end{aligned}$
张量并行组中Rank0持有 $X_1$ 和 $A_1$ ，Rank1持有 $X_2$ 和 $A_2$ ，并在各自的GPU上完成前向传播后再合并起来。

反向传播的过程
$KaTeX parse error: Undefined control sequence: \part at position 8: \frac{\̲p̲a̲r̲t̲ ̲f}{\part X_1} =…$

源代码

class RowParallelLinear(torch.nn.Module):
    """
    行并行线性层.
    线性层的定义为Y = XA + b. x
    A沿着第一个维度并行，X沿着第二个维度并行. 即
               -   -
              | A_1 |
              | .   |
          A = | .   |        X = [X_1, ..., X_p]
              | .   |
              | A_p |
               -   -
    参数:
        input_size: 矩阵A的第一维度.
        output_size: 矩阵A的第二维度.
        bias: 若为true则添加bias.
        input_is_parallel:  若为true，则认为输入应用被划分至各个GPU上，不需要进一步的划分.
    	init_method: 随机初始化方法.
    	stride: strided线性层.
    """

    def __init__(self, input_size, output_size, bias=True,
                 input_is_parallel=False,
                 init_method=init.xavier_normal_, stride=1,
                 keep_master_weight_for_test=False,
                 skip_bias_add=False):
        super(RowParallelLinear, self).__init__()

        self.input_size = input_size
        self.output_size = output_size
        self.input_is_parallel = input_is_parallel
        # 获得张量并行组的world_size
        world_size = get_tensor_model_parallel_world_size()
        # 按照张量并行度(world_size)划分输出维度
        self.input_size_per_partition = divide(input_size, world_size)
        self.skip_bias_add = skip_bias_add

        # Parameters.
        # Note: torch.nn.functional.linear 执行 XA^T+b
        args = get_args()
        if args.use_cpu_initialization:
            # 初始化张量. 若完整权重矩阵A为n*m，张量并行度为k，这里初始化的张量为n*(m/k)
            # 也就是张量并行组中的进程各自初始化持有的部分张量
            self.weight = Parameter(torch.empty(self.output_size,
                                                self.input_size_per_partition,
                                                dtype=args.params_dtype))
            # 使用init_method对权重矩阵self.weight进行随机初始化(CPU版)
            # self.master_weight在测试中使用，这里不需要关注
            self.master_weight = _initialize_affine_weight_cpu(
                self.weight, self.output_size, self.input_size,
                self.input_size_per_partition, 1, init_method,
                stride=stride, return_master_weight=keep_master_weight_for_test)
        else:
            self.weight = Parameter(torch.empty(
                self.output_size, self.input_size_per_partition,
                device=torch.cuda.current_device(), dtype=args.params_dtype))
            # 使用init_method对权重矩阵self.weight进行随机初始化(GPU版)
            _initialize_affine_weight_gpu(self.weight, init_method,
                                          partition_dim=1, stride=stride)
        if bias:
            # 实例化一个bias
            if args.use_cpu_initialization:
                self.bias = Parameter(torch.empty(self.output_size,
                                                  dtype=args.params_dtype))
            else:
                self.bias = Parameter(torch.empty(
                    self.output_size, device=torch.cuda.current_device(),
                    dtype=args.params_dtype))
            # Always initialize bias to zero.
            with torch.no_grad():
                self.bias.zero_()
        else:
            self.register_parameter('bias', None)

        self.bias_tp_auto_sync = args.sync_tp_duplicated_parameters

    def forward(self, input_):
        if self.input_is_parallel:
            input_parallel = input_
        else:
            # 前向传播时，将input_分片至张量并行组中的各个进程中
            # 反向传播时，将张量并行组中持有的部分input_梯度合并为完整的梯度
            # 此时，_input是完整的输入张量，input_parallel则是分片后的张量，即input_parallel!=_input
            input_parallel = scatter_to_tensor_model_parallel_region(input_)
        
        output_parallel = F.linear(input_parallel, self.weight)
        # 对张量并行组中的输出进行allreduce，即操作X1A1+X2A2
        output_ = reduce_from_tensor_model_parallel_region(output_parallel)

        if self.bias_tp_auto_sync:
            torch.distributed.all_reduce(self.bias, op=torch.distributed.ReduceOp.AVG, group=mpu.get_tensor_model_parallel_group())

        if not self.skip_bias_add:
            output = output_ + self.bias if self.bias is not None else output_
            output_bias = None
        else:
            output = output_
            output_bias = self.bias
        return output, output_bias

测试代码

由于列并行层RowParallelLinear完成屏蔽了内部的并行细节，无法从输入输出中理解其执行过程。因此，这里的测试会对其forward方法进行重写，以便展现细节。

class MyRowParallelLinear(mpu.RowParallelLinear):
    def forward(self, input_):
        global_rank = torch.distributed.get_rank()
        # 输入X，权重A和输出Y的形状
        X_size = list(input_.size())
        A_size = [self.input_size, self.output_size]
        Y_size = [X_size[0], A_size[1]]
        if self.input_is_parallel:
            input_parallel = input_
        else:
            input_parallel = mpu.scatter_to_tensor_model_parallel_region(input_)
        Xi_size = list(input_parallel.size())
        Ai_size = list(self.weight.T.size())

        info = f"*"*20 + \
                f"\n> global_rank={global_rank}\n" + \
                f"> size of X={X_size}\n" + \
                f"> size of A={A_size}\n" + \
                f"> size of Y={Y_size}\n" + \
                f"> size of Xi={Xi_size}\n" + \
                f"> size of Ai={Ai_size}\n"

        output_parallel = F.linear(input_parallel, self.weight)
        # 通过在output_parallel保证不同rank的output_parallel，便于观察后续的结果
        output_parallel = output_parallel + global_rank
        Yi_size = list(output_parallel.size())
        info += f"> size of Yi={Yi_size}\n" + \
                f"> Yi={output_parallel}\n"
        output_ = mpu.reduce_from_tensor_model_parallel_region(output_parallel)
        info += f"> Y={output_}"

        if self.bias_tp_auto_sync:
            torch.distributed.all_reduce(self.bias, op=torch.distributed.ReduceOp.AVG, group=mpu.get_tensor_model_parallel_group())

        if not self.skip_bias_add:
            output = output_ + self.bias if self.bias is not None else output_
            output_bias = None
        else:
            output = output_
            output_bias = self.bias
        print(info)
        return output, output_bias
    
def test_row_parallel_linear():
    global_rank = torch.distributed.get_rank()
    tensor_model_parallel_size = mpu.get_tensor_model_parallel_world_size()
    # 设置随机种子
    seed = 12345
    set_random_seed(seed)
     # 张量并行组中，各个进程持有张量的input_size
    input_size_coeff = 4
    input_size = input_size_coeff * tensor_model_parallel_size
     # 张量并行组中，各个进程持有张量的output_size
    output_size_coeff = 2
    output_size = output_size_coeff * tensor_model_parallel_size
    # 初始化一个产生二维张量的模拟网络，输入的张量为(batch_size, input_size)
    batch_size = 6
    identity_layer = IdentityLayer2D(batch_size, input_size).cuda()
    # 初始化一个行并行线性层
    linear_layer = MyRowParallelLinear(
        input_size, output_size, keep_master_weight_for_test=True).cuda()

    # 前向传播
    input_ = identity_layer()
    output = linear_layer(input_)

测试结果

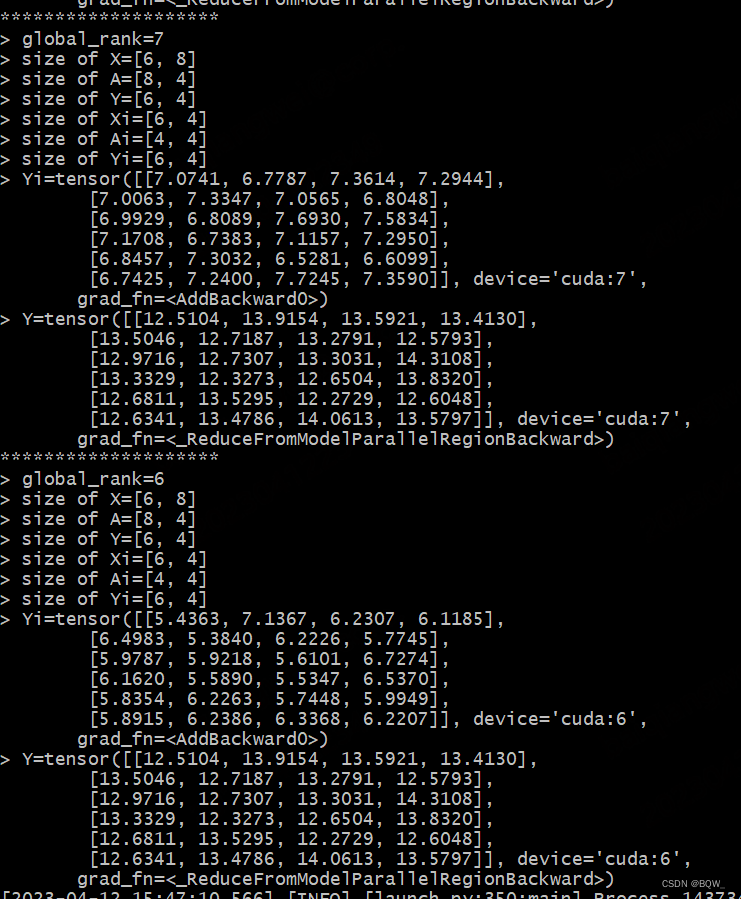
在这里插入图片描述

四、完整测试代码

# test_layers.py
import sys
sys.path.append("..")

import os
import torch.nn.functional as F
from megatron import get_args
from megatron.mpu import layers
from megatron.initialize import _initialize_distributed
from megatron.global_vars import set_global_variables
from commons import set_random_seed
from commons import print_separator
from commons import initialize_distributed
import megatron.mpu as mpu
import torch.nn.init as init
from torch.nn.parameter import Parameter
import torch
import random

class IdentityLayer2D(torch.nn.Module):
    """
    模拟一个输入为二维张量的神经网络
    """
    def __init__(self, m, n):
        super(IdentityLayer2D, self).__init__()
        self.weight = Parameter(torch.Tensor(m, n))
        torch.nn.init.xavier_normal_(self.weight)

    def forward(self):
        return self.weight
    
def test_column_parallel_linear():
    global_rank = torch.distributed.get_rank()
    tensor_model_parallel_size = mpu.get_tensor_model_parallel_world_size()
    # 设置随机数种子
    seed = 12345
    set_random_seed(seed)
    # 张量并行组中，各个进程持有张量的input_size
    input_size_coeff = 4 #
    # 张量并行组中，各个进程持有张量的output_size
    input_size = input_size_coeff * tensor_model_parallel_size
    output_size_coeff = 2
    output_size = output_size_coeff * tensor_model_parallel_size
    # 初始化一个产生二维张量的模拟网络，输入的张量为(batch_size, input_size)
    batch_size = 6
    identity_layer = IdentityLayer2D(batch_size, input_size).cuda()
    # 初始化一个列并行线性层
    linear_layer = mpu.ColumnParallelLinear(
        input_size, output_size, keep_master_weight_for_test=True, gather_output=False).cuda()
    # 随机初始化一个loss权重
    # 主要是为了计算标量的loss，从而验证梯度是否正确
    loss_weight = torch.randn([batch_size, output_size]).cuda()
    ## 前向传播
    input_ = identity_layer()
    # 此时，张量并行组中各个进程持有的output仅是完整输出张量的一部分
    output = linear_layer(input_)[0]

    if torch.distributed.get_rank() == 0:
        print(f"> Output size without tensor parallel is ({batch_size},{output_size})")
    torch.distributed.barrier()
    info = f"*"*20 + \
            f"\n> global_rank={global_rank}\n" + \
            f"> output size={output.size()}\n"
    print(info, end="")
    
class MyRowParallelLinear(mpu.RowParallelLinear):
    def forward(self, input_):
        global_rank = torch.distributed.get_rank()
        # 输入X，权重A和输出Y的形状
        X_size = list(input_.size())
        A_size = [self.input_size, self.output_size]
        Y_size = [X_size[0], A_size[1]]
        if self.input_is_parallel:
            input_parallel = input_
        else:
            input_parallel = mpu.scatter_to_tensor_model_parallel_region(input_)
        Xi_size = list(input_parallel.size())
        Ai_size = list(self.weight.T.size())

        info = f"*"*20 + \
                f"\n> global_rank={global_rank}\n" + \
                f"> size of X={X_size}\n" + \
                f"> size of A={A_size}\n" + \
                f"> size of Y={Y_size}\n" + \
                f"> size of Xi={Xi_size}\n" + \
                f"> size of Ai={Ai_size}\n"

        output_parallel = F.linear(input_parallel, self.weight)
        # 通过在output_parallel保证不同rank的output_parallel，便于观察后续的结果
        output_parallel = output_parallel + global_rank
        Yi_size = list(output_parallel.size())
        info += f"> size of Yi={Yi_size}\n" + \
                f"> Yi={output_parallel}\n"
        output_ = mpu.reduce_from_tensor_model_parallel_region(output_parallel)
        info += f"> Y={output_}"

        if self.bias_tp_auto_sync:
            torch.distributed.all_reduce(self.bias, op=torch.distributed.ReduceOp.AVG, group=mpu.get_tensor_model_parallel_group())

        if not self.skip_bias_add:
            output = output_ + self.bias if self.bias is not None else output_
            output_bias = None
        else:
            output = output_
            output_bias = self.bias
        print(info)
        return output, output_bias
    
def test_row_parallel_linear():
    global_rank = torch.distributed.get_rank()
    tensor_model_parallel_size = mpu.get_tensor_model_parallel_world_size()
    # 设置随机种子
    seed = 12345
    set_random_seed(seed)
     # 张量并行组中，各个进程持有张量的input_size
    input_size_coeff = 4
    input_size = input_size_coeff * tensor_model_parallel_size
     # 张量并行组中，各个进程持有张量的output_size
    output_size_coeff = 2
    output_size = output_size_coeff * tensor_model_parallel_size
    # 初始化一个产生二维张量的模拟网络，输入的张量为(batch_size, input_size)
    batch_size = 6
    identity_layer = IdentityLayer2D(batch_size, input_size).cuda()
    # 初始化一个行并行线性层
    linear_layer = MyRowParallelLinear(
        input_size, output_size, keep_master_weight_for_test=True).cuda()

    # 前向传播
    input_ = identity_layer()
    output = linear_layer(input_)

def main():
    set_global_variables(ignore_unknown_args=True)
    _initialize_distributed()
    world_size = torch.distributed.get_world_size()

    print_separator('Test test_column_parallel_linear')
    test_column_parallel_linear()

    print_separator('Test test_row_parallel_linear')
    test_row_parallel_linear()


if __name__ == '__main__':
    main()

启动脚本

# 除了tensor-model-parallel-size和pipeline-model-parallel-size以外，
# 其余参数仅为了兼容原始代码，保存没有报错.
options=" \
        --tensor-model-parallel-size 2 \
        --pipeline-model-parallel-size 2 \
        --num-layers 10 \
        --hidden-size 768 \
        --micro-batch-size 2 \
        --num-attention-heads 32 \
        --seq-length 512 \
        --max-position-embeddings 512\
        --use_cpu_initialization True
        "

cmd="deepspeed test_layers.py $@ ${options}"

eval ${cmd}