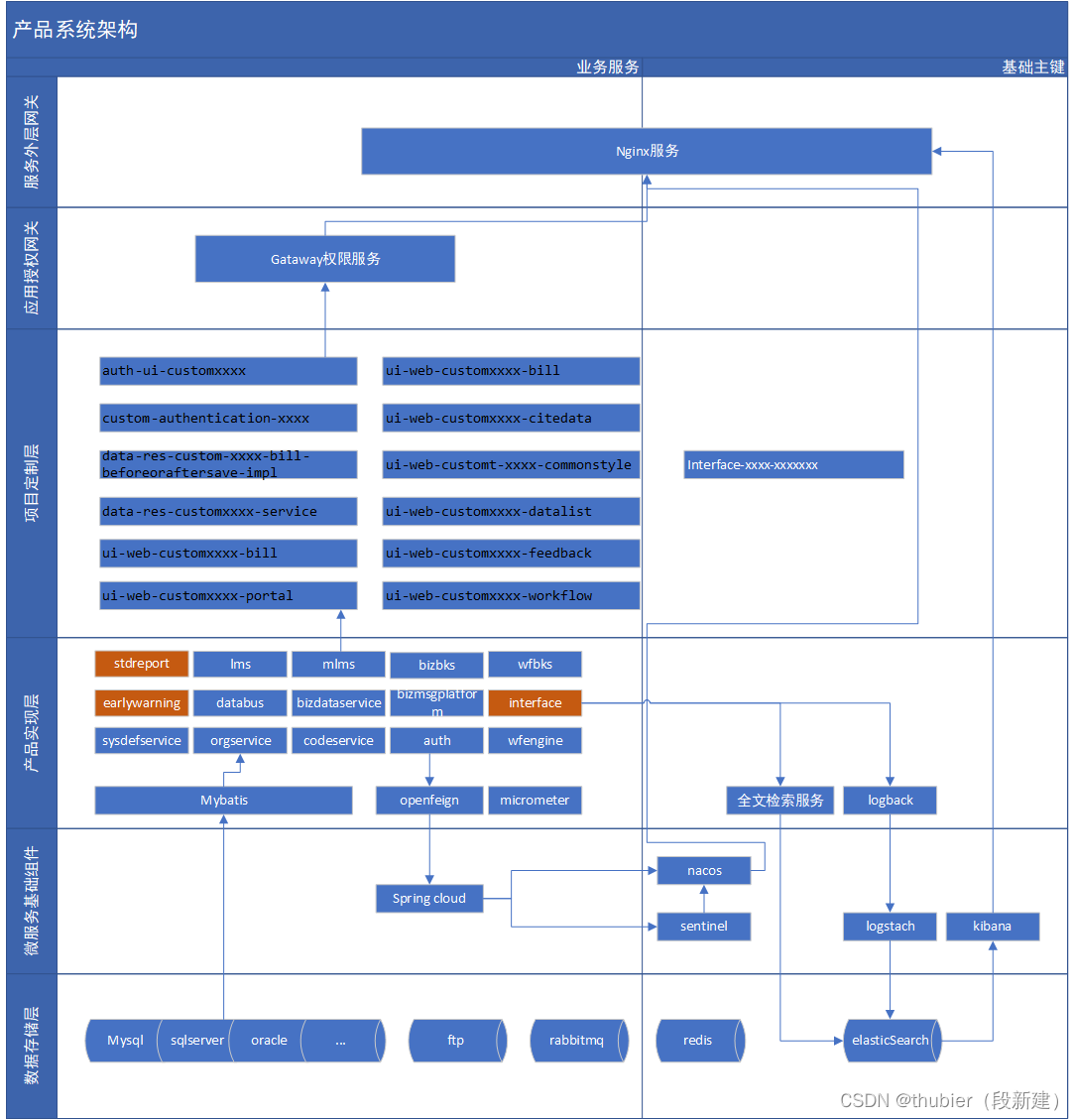
题目

思路

直接模拟排序肯定会TLE，所以我们想一种离线的方法：01排序
利用二分答案check一下d，设序列中大于等于d的数为1，小于d的数为0
完成后再进行排序：这样升序排列就是将0放前面1放后面，降序排列则相反
“放”这一操作还可以优化：降序排序中，先输出一共有num个1，然后把前num个数设成1，后面的数设成0，升序排列则相反
在全部模拟完后，我们看看第q位上的数是0还是1，若是1，则代表$a_q$是大于等于二分答案d，也就是说需要将l右移，反之左移
证明：$a_q>=d,若使二分答案d更接近最终答案，需要将d增大，也就是l=mid+1$
因为用到了区间操作，所以我们用线段树做
理论存在，实践开始

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define INF 0x3f3f3f3f
const int M=1e7+5;
struct node{
	int opt,l,r;
}qs[M];
istream& operator >> (istream& in,node& t){
	in>>t.opt>>t.l>>t.r;
	return in;
}
int a[M];
int n,m;
int q;
int maxn=-INF;
struct seg{
	#define lc(x) x<<1
	#define rc(x) x<<1|1
	int tag[M<<2],v[M<<2];
	bool vis[M<<2];
	void cover(int x,int l,int r,int k){//记录tag+更改操作
		tag[x]=k,vis[x]=1;
		v[x]=k*(r-l+1);
	}
	void pushup(int x) { v[x]=v[lc(x)]+v[rc(x)]; }//向上更改
	void pushdown(int x,int l,int r){//向下更改
		if(!vis[x]) return;
		int mid=l+r>>1;
		cover(lc(x),l,mid,tag[x]),cover(rc(x),mid+1,r,tag[x]);
		tag[x]=0,vis[x]=0;
	}
	void build(int x,int l,int r,int k){//建树
		vis[x]=0;
		if(l==r) { v[x]=(a[l]>=k);return; }
		int mid=l+r>>1;
		build(lc(x),l,mid,k),build(rc(x),mid+1,r,k);
		pushup(x);
	}
	int query(int ql,int qr,int x,int l,int r){//查询区间和的数量
		if(ql>qr) return 0;//特殊情况判断
		if(ql<=l&&r<=qr) return v[x];
		int ans=0;
		int mid=l+r>>1;
		pushdown(x,l,r);
		if(ql<=mid) ans+=query(ql,qr,lc(x),l,mid);//特殊情况
		if(mid+1<=qr) ans+=query(ql,qr,rc(x),mid+1,r);
		pushup(x);
		return ans;
	}
	void update(int ql,int qr,int x,int l,int r,int k){
		if(ql>qr) return;
		if(ql<=l&&r<=qr) { cover(x,l,r,k);return; }
		pushdown(x,l,r);
		int mid=l+r>>1;
		if(ql<=mid) update(ql,qr,lc(x),l,mid,k);
		if(mid+1<=qr) update(ql,qr,rc(x),mid+1,r,k);
		pushup(x);
	}
}st;
bool check(int d){
	st.build(1,1,n,d);
	int num;
	for(int i=1;i<=m;i++){
		int l=qs[i].l;int r=qs[i].r;
		num=st.query(l,r,1,1,n);
		switch (qs[i].opt){
			case 1:st.update(l,l+num-1,1,1,n,1),st.update(l+num,r,1,1,n,0);break;//升序（前1后0）
			case 0:num=r-l+1-num;st.update(l,l+num-1,1,1,n,0),st.update(l+num,r,1,1,n,1);break;//降序（前0后1）
		}
	}
	return st.query(q,q,1,1,n);//查询a[q]的值
}
signed main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i],maxn=max(maxn,a[i]);
	for(int i=1;i<=m;i++) cin>>qs[i];
	cin>>q;
	int l=1,r=maxn,ans;
	while(l<=r){
		int mid=l+r>>1;
		if(check(mid)) l=mid+1,ans=mid;
		else r=mid-1;
	}
	cout<<ans;
	return 0;
}