栈和队列的简单介绍
栈
栈是一个“先进后出”结构

队列
入队演示
队列是一种“先进先出”的结构
出队演示
接下来我们开始本次的内容
栈实现队列
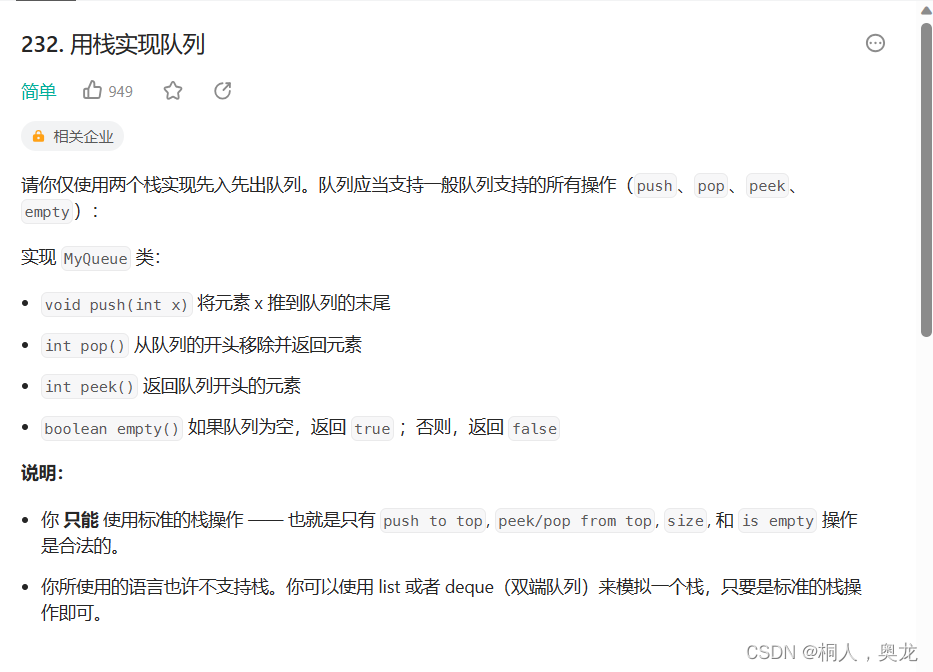
分析
1.我们可以老老实实的写一个栈然后将所有的接口函数实现出来,最后再进行实现队列,但是显然是效率低下的方法
2.我们使用数组模拟栈,然后再进行实现队列—可行
3.或者直接使用STL
算法演示

开始实现
class MyQueue {
public:
//我们不需要使用他的函数,因为我不想传参
//定义两个stack一个是输入栈,一个是输出栈
stack<int> pushst;
stack<int> popst;
MyQueue() {
}
//将元素输入到输入栈中
void push(int x) {
pushst.push(x);
}
int pop() {
int res;//定义一个int型的值,用来接受返回值
//pop的时候是从输出栈的栈顶出数据
//如果输出栈为空,判断输入栈有没有数据,只有输入栈有数据的时候才能进行转移
//只有输出栈有数据才能进行pop
//我们可以将顺序进行转换,但是需要进行重复的步骤
//也就是说,1.一开始popst没有元素为空,
//2.pushst有值,将pushst的元素转移到popst中,
//3.在进行popst不为空的判断进行pop那么
//1.3步是相同的操作,如果将2换到最前面,后面只需要紧跟一个1步骤就能完成操作
if(!popst.size())
{
while(pushst.size())
{
popst.push(pushst.top());
pushst.pop();
}
}
if(popst.size())
res=popst.top(),popst.pop();
return res;
}
//同上
int peek() {
int res;
if(!popst.size())
{
while(pushst.size())
{
popst.push(pushst.top());
pushst.pop();
}
}
if(popst.size())
res=popst.top();
return res;
}
//当pushst和popst同时没有值的时候->空
bool empty() {
if(pushst.size()||popst.size()) return false;
return true;
}
};
队列实现栈
算法演示
进栈
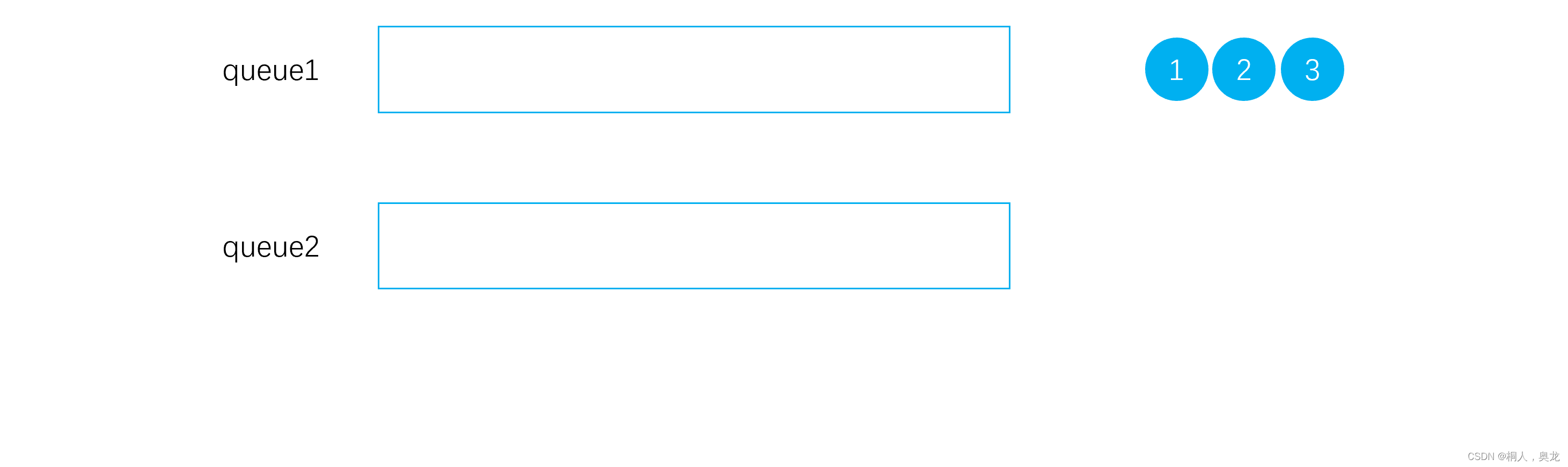
出栈

开始实现
c++中queue是双端队列,但是我们不适用这个特性,我们一点点的实现
class MyStack {
public:
queue<int> q1,q2;
MyStack() {
}
//使用假设的方式,定义空队列,进行判断是否与自己的假设相反,再空的队列中添加元素
void push(int x) {
queue<int>* em=&q1,*noem=&q2;
if(!em->size()) noem=em,em=&q2;
em->push(x);
}
//在pop的时候需要将不为空的队列找到,然后使队列中只剩一个元素,其余的元素全部移入另一个队列中,最后将这个元素记录并且删除
int pop() {
queue<int>* em=&q1,*noem=&q2;
if(!noem->size()) em=noem,noem=&q1;
while(noem->size()>1)
{
em->push(noem->front());
noem->pop();
}
int res=0;
if(noem->size()==1)
{
res=noem->front();
noem->pop();
}
return res;
}
//同上
int top() {
queue<int>* em=&q1,*noem=&q2;
if(!noem->size()) em=noem,noem=&q1;
while(noem->size()>1)
{
em->push(noem->front());
noem->pop();
}
int res=0;
if(noem->size()==1)
{
res=noem->front();
em->push(noem->front());
noem->pop();
}
return res;
}
bool empty() {
if(q1.size()||q2.size()) return false;
return true;
}
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/
设计循环队列

算法演示

开始实现
//使用数组进行实现,结构体需要包含数组,实际使用的空间个数,头,尾
typedef struct {
int* a;
int k;
int hh,tt;
} MyCircularQueue;
//当头和尾重合的时候就是空的时候
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->hh==obj->tt;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->tt+1)%(obj->k+1)==obj->hh ;
}
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* queue=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
queue->a=(int*)malloc(sizeof(int)*(k+1));
queue->k=k;
queue->hh=queue->tt=0;
return queue;
}
//对特殊情况进行判断,当tt位于最后一个的时候,需要将他从重新置为开头
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj)) return false;
obj->a[obj->tt++]=value;
obj->tt%=(obj->k+1);
return true;
}
//对特殊情况进行判断,当hh位于最后一个的时候,需要将他从重新置为开头
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj)) return false;
obj->hh++;
obj->hh%=(obj->k+1);
return true;
}
//如果为空直接返回-1,不为空返回相应的值
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj)) return -1;
return obj->a[obj->hh];
}
//最后一个数据是在tt的前一个位置,同时当tt位于开头的时候需要找到最后的位置找值
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj)) return -1;
return obj->a[(obj->tt+obj->k)%(obj->k+1)];
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}
/**
* Your MyCircularQueue struct will be instantiated and called as such:
* MyCircularQueue* obj = myCircularQueueCreate(k);
* bool param_1 = myCircularQueueEnQueue(obj, value);
* bool param_2 = myCircularQueueDeQueue(obj);
* int param_3 = myCircularQueueFront(obj);
* int param_4 = myCircularQueueRear(obj);
* bool param_5 = myCircularQueueIsEmpty(obj);
* bool param_6 = myCircularQueueIsFull(obj);
* myCircularQueueFree(obj);
*/