1.选择排序

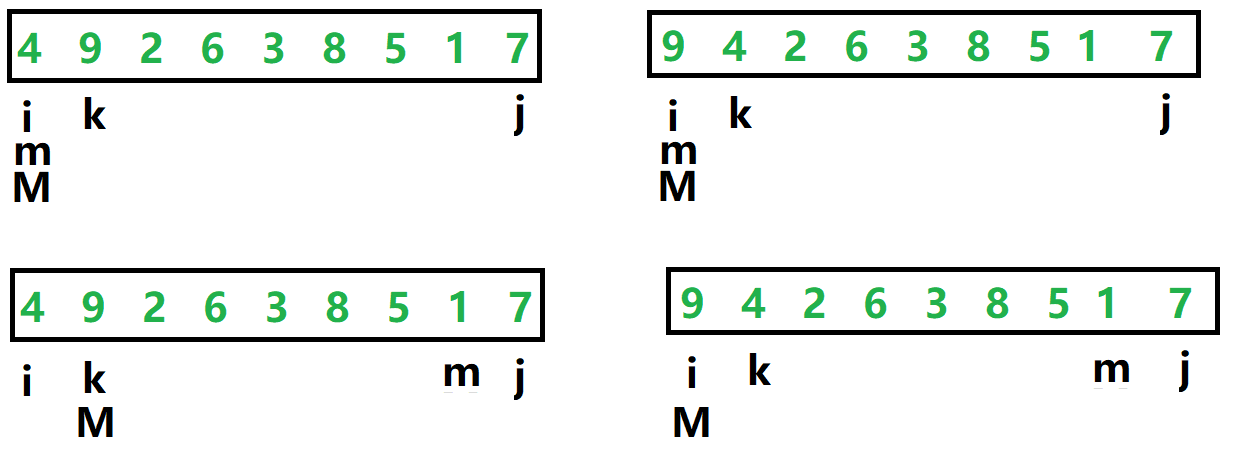
在这里插入图片描述

1.1代码实现

// 当数据趋于有序或随机(可能部分有序) 插排更有优势 O(N)~O(N^2)
//选择排序：O（N^2）                               O(N^2)~O(N^2)
void SelectSort(int* a, int n)
{
	assert(a);
	//i：数据头 j：数据尾
	for (int i = 0, j = n - 1; i < j; ++i, --j)
	{
		//假设最大值/最小值下标为i
		int m = i, M = i;
		//遍历i后到j的所有数据 确定real_m/M
		for (int k = i + 1; k <= j; ++k)
		{
			if (a[k] < a[m])
				m = k;

			if (a[k] > a[M])
				M = k;
		}
		//小值换到数据头
		Swap(&a[i], &a[m]);
		//特殊情况需重新匹配
		if (i == M)
		{
			M = m;
		}
		//大值换到数据尾
		Swap(&a[j], &a[M]);
	}
}

1.2复杂度

在这里插入图片描述

2.堆排序

2.1代码实现

//堆排序 -- 升序建大堆 降序建小堆
void AdjustDwon(int* a, int size, int parent)
{
	//设左孩子较小
	int child = parent * 2 + 1;
	//当未达到堆末 进入循环
	while (child < size)
	{
		//确定real小孩子
		//if (child + 1 < size && a[child + 1] < a[child])  //小堆
		
		//确定real大孩子
		if (child + 1 < size && a[child + 1] > a[child])    //大堆
		{
			++child;
		}
		
		//if (a[parent] > a[child])    //小堆
		if (a[parent] < a[child])      //大堆
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	//下调建大堆
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDwon(a, n, i);
	}
	//排序
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDwon(a, end, 0);
		--end;
	}
}