💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码实现
💥1 概述
1.1 基于热传导 (ED-HC) 的边缘检测旨在揭示或锐化红外图像中物体的边缘。
1.2 ED-HC的功能旨在根据红外图像中表面温度的条件和热流特性进行边缘检测。
1.3 热电偶校基于热传导基质。
1.4 HCM是一个特征矩阵,将固体和静止流体的热传导公式应用于红外图像,并检查相邻像素之间的差异值。
1.5 通过将ED-HC方法应用于灰度图像,该方法已被证明对灰度图像有效。
1.6 ED-HC方法在模糊度过高,亮度对比度低的红外图像中具有很强的性能。
📚2 运行结果
主函数代码:
clear all;
close all;
clc;
tic
%---------------------------------------------------------------------------
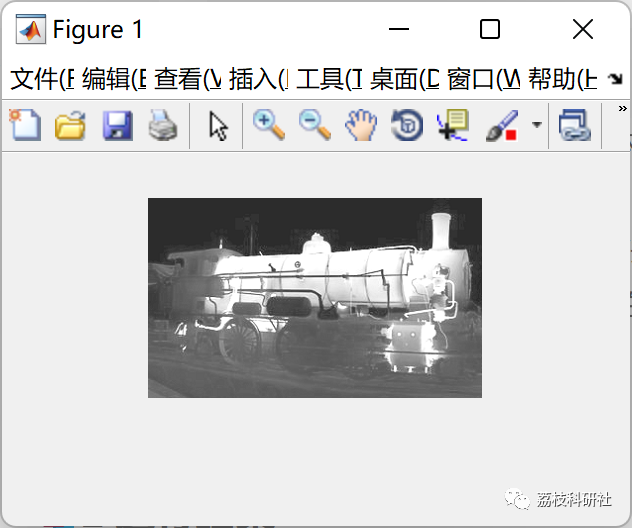
img = imread('K6.png');
img=rgb2gray(img);
img=imresize(img,1);
figure; imshow(img);
% STEP 1:Calculation of the average heat conduction matrix
%------------------------------------------------------------------------------------------
img1=img;
h=size(img1,1);
w=size(img1,2);
heatmat=zeros(h,w);
for i=2: (h-2);
for j=2: (w-2);
maskGray=zeros(1,9) ;
for b=1:9;
[x]=ikomsu(b,i);
[y]=jkomsu(b,j);
col = img1(x,y);
maskGray (b) =col;
end
[heat_top]=heattrans(maskGray);
heatmat(i,j)=heat_top;
end
end
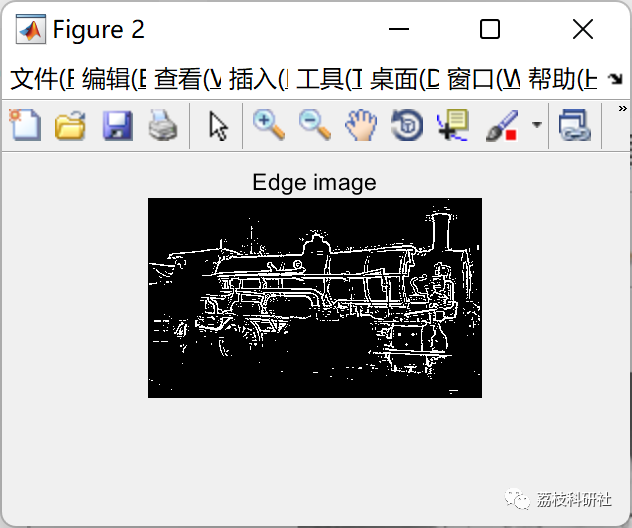
% STEP 2:Edge Detection
%--------------------------------------------------------------------------------------------
for i=2: (h);
for j=2: (w);
if(heatmat(i,j)>100)
edge_im(i,j)=255;
else
edge_im(i,j)=0;
end
end
end
edge_im=uint8(edge_im);
figure; imshow(edge_im); title('Edge image');
toc
%-------------------------------------------------------------------------
% STEP 3: Image Quality Assessment for Edge Detection Aplication
%1.ESSIM
[ESSIM_index] = ESSIM(img,edge_im)
%2. IoU
IoU_Value=iou(img,edge_im)
%3. NCC
NCC_Value=NormalizedCrossCorrelation(img,edge_im)
%4.Edge Intensity
enh1 = sobel_enh_conv(edge_im);
edge_intensity = sum(enh1(:))
%-----------------------------------------------------------------------------------
%FUNCTIONS
%-----------------------------------------------------------------------------------
function [x] = ikomsu( komsuno, i)
if(komsuno ==1)
x=i-1;
elseif(komsuno ==2)
x= i;
elseif(komsuno ==3)
x= i+1;
elseif(komsuno ==4)
x= i-1;
elseif(komsuno ==5)
x= i+1;
elseif(komsuno ==6)
x= i-1;
elseif(komsuno ==7)
x= i;
elseif(komsuno ==8)
x= i+1;
else
x=i;
end
end
function [y] = jkomsu( komsuno, j )
if(komsuno ==1)
y= j-1;
elseif(komsuno ==2)
y= j-1;
elseif(komsuno ==3)
y= j-1;
elseif(komsuno ==4)
y= j;
elseif(komsuno ==5)
y= j;
elseif(komsuno ==6)
y= j+1;
elseif(komsuno ==7)
y= j+1;
elseif(komsuno ==8)
y= j+1;
else
y= j;
end
end
function [ESSIM_index] = ESSIM(Ref_img, Dis_img)
Ref_img = double(Ref_img);
Dis_img = double(Dis_img);
if size(Ref_img,3)==3
Ref_img = 0.299 * double(Ref_img(:,:,1)) + 0.587 * double(Ref_img(:,:,2)) + 0.114 * double(Ref_img(:,:,3));
Dis_img = 0.299 * double(Dis_img(:,:,1)) + 0.587 * double(Dis_img(:,:,2)) + 0.114 * double(Dis_img(:,:,3));
end
[M,N]=size(Ref_img);
f = max(1,round(min(M,N)/256));
%downsampling by f
%use a simple low-pass filter
if(f>1)
lpf = ones(f,f);
lpf = lpf/sum(lpf(:));
Ref_img = imfilter(Ref_img,lpf,'symmetric','same');
Dis_img = imfilter(Dis_img,lpf,'symmetric','same');
Ref_img = Ref_img(1:f:end,1:f:end);
Dis_img = Dis_img(1:f:end,1:f:end);
end
[m,n]=size(Ref_img);
% Fractional gradient
[g1]=directional_gradient(Ref_img);
[g2]=directional_gradient(Dis_img);
L=255;
alfa=0.5;
K(1)=10;
C1 = (K(1)*L).^(2*alfa);
grad1=abs(g1(:,:,[1,3])-g1(:,:,[2,4])).^alfa;
grad2=abs(g2(:,:,[1,3])-g2(:,:,[2,4])).^alfa;
[Y X]=meshgrid(1:n,1:m);
[x ind3]=max(grad1,[],3);
ind=sub2ind([m,n,2],X(:),Y(:),ind3(:));
map=(2*grad1(ind).*grad2(ind)+C1)./(grad1(ind).^2+grad2(ind).^2+C1);
ESSIM_index=mean(map(:));
end
function [g]=directional_gradient(f)
[m,n]=size(f);
g=zeros(m,n,4);
K1=zeros(5);K2=K1; K3=K1; K4=K1;
Kt=1/16*[3 10 3;0 0 0; -3 -10 -3];
K1(2:4,2:4)=Kt; K2=K1';
K3=1/16*[ 0 0 3 0 0;
0 10 0 0 0;
3 0 0 0 -3;
0 0 0 -10 0;
0 0 -3 0 0];
K4=rot90(K3);
g(:,:,1)=filter2(K1,f,'same');
g(:,:,2)=filter2(K2,f,'same');
g(:,:,3)=filter2(K3,f,'same');
g(:,:,4)=filter2(K4,f,'same');
end
function d = iou(in1,in2)
% inputs are bounding box vectors
if (isvector(in1) && numel(in1) == 4) && (isvector(in2) && numel(in2) == 4)
intersectionBox = [max(in1(1:2), in2(1:2)), min(in1(3:4), in2(3:4))];
iw = intersectionBox(3)-intersectionBox(1)+1;
ih = intersectionBox(4)-intersectionBox(2)+1;
if iw>0 && ih>0
% compute overlap as area of intersection / area of union
unionArea = (in1(3)-in1(1)+1)*(in1(4)-in1(2)+1)+...
(in2(3)-in2(1)+1)*(in2(4)-in2(2)+1)- iw*ih;
d = iw*ih/unionArea;
else
d = 0;
end
% inputs are bounding box matrices
elseif size(in1,2) == 4 && size(in2,2) == 4
intersectionBox = [max(in1(:,1), in2(:,1)), max(in1(:,2), in2(:,2)),...
min(in1(:,3), in2(:,3)), min(in1(:,4), in2(:,4))];
iw = intersectionBox(:,3)-intersectionBox(:,1)+1;
ih = intersectionBox(:,4)-intersectionBox(:,2)+1;
unionArea = bsxfun(@minus, in1(:,3), in1(:,1)-1) .*...
bsxfun(@minus, in1(:,4), in1(:,2)-1) +...
bsxfun(@minus, in2(:,3), in2(:,1)-1) .*...
bsxfun(@minus, in2(:,4), in2(:,2)-1) - iw.*ih;
d = iw .* ih ./ unionArea;
d(iw <= 0 | ih <= 0) = 0;
% inputs are binary masks
elseif ismatrix(in1) && ismatrix(in2)
assert(isequal(size(in1),size(in2)),'Masks must have the same dimensions')
u = nnz(in1 | in2);
if u > 0
d = nnz(in1 & in2) / u;
else
d = 0;
end
else
error('Input must be two logical masks or two bounding box vector/matrices')
end
end
function NK = NormalizedCrossCorrelation(origImg, distImg)
origImg = double(origImg);
distImg = double(distImg);
NK = sum(sum(origImg .* distImg)) / sum(sum(origImg .* origImg));
end
function s = sobel_enh_conv (image)
m = [-1 -2 -1;0 0 0;1 2 1];
m2 = m';
i = image;
[si1 si2] = size(i);
result = conv2(m,i);
result1 = conv2 (m2,i);
result = result(2:si1+1, 2:si2+1);
result1 = result1(2:si1+1, 2:si2+1);
% SOBEL EDGE DETECTION
result1 = result1.^2;
result = result.^2;
final = result1 + result;
final = final.^(0.5);
s = final;
end
🎉3 参考文献
[1]Katırcıoğlu, F. (2020). Edge detection method based on heat conduction matrix for infrared images. Optical Engineering, 59(9), 093103.